⤓ Deduktiv argumentasjon#
Forutsetninger og læringsmål#
Introduksjon#
Deduksjon er å bruke regler til å utlede at en konklusjon er sann gitt premisser. Noen vil si at bare deduktiv argumentasjon fortjener å kalles bevis.
En deduksjon kan altså være
En likningsløsning (f.eks. hvor premisset er påstanden \(x^2 = 5 - 4x\) og konklusonen er påstanden \(x = 1 ∨ x = -5\); aktuelle regler kan være likningsregler og abc-formelen).
Et bevis, f.eks. for at det finnes uendelig mange primtall
Premiss og konklusjon#
Bevis starter i et (eller flere) påstander som kalles premiss, og ender med en påstand som er konklusjonen. Regler fra premiss til konklusjon gjør at man (om argumentasjonen er gyldig, da) kan være sikker på at om premissene er sanne er også konklusjonen sann.
Har vi flere premisser må vi selvsagt være sikker på at alle premissene er sanne før vi kan garantere at konklusjonen er sann.
Et bevis bruker/inneholder tidligere kjente regler#
Et bevis bruker regelen vi tror på fra før.
Eksempel: abc-regelen Vi kan bevise abc-regelen på liknende måte. Vi begynner med en utregning som bruker kjente regler inni. Når vi vet at vi kan gå fra premisset (her: \(ax^2 + bx + c = 0\)) til konklusjonen (her: \(x = \frac{-b ±\sqrt{b^2 - 4ab}}{2a}\)) kan vi så gjøre det til en generell regel.
\(ax^2 + bx + c = 0\)
\(\small ↓\)
\(x^2 + \frac{b}{a}x + \frac{c}{a} = 0\)
\(\small ↓\)
\(x^2 + \frac{b}{a}x = −\frac{c}{a}\)
\(\small ↓\) Vi legger altså til \( \left(\frac{b}{2a}\right)²\) for å “fullføre kvadratet”
\(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)² = −\frac{c}{a} + \left(\frac{b}{2a}\right)²\)
\(\small ↓\) Lettere å se om man regner baklengs?
\(\small ↓\)\(\left(x + \frac{b}{2a}\right)² = \frac{-c}{a} + \left(\frac{b}{2a}\right)²\)
\(\small ↓\) Utvider brøker
\(\left(x + \frac{b}{2a}\right)² = \frac{-4ac}{4a²} + \frac{b²}{4a²}\)
\(\small ↓\)
\(\left(x + \frac{b}{2a}\right)² = \frac{b² -4ac}{4a²}\)
\(\small ↓\) Kvadratrot på begge sider
\(x + \frac{b}{2a} = ±\sqrt{\frac{b² -4ac}{4a²}}\)
\(\small ↓\)
\(x = -\frac{b}{2a} + \frac{±\sqrt{b² -4ac}}{\sqrt{4a²}}\)
\(\small ↓\)
\(x = -\frac{b}{2a} + \frac{±\sqrt{b² -4ac}}{2a}\)
\(\small ↓\)
\(x = \frac{-b ±\sqrt{b^2 - 4ab}}{2a}\)
(Mange vil oppleve at utregningen ser grei ut, om vi følger det ledd for ledd; men det er vanskelig å forstå prosessen med å komme fram til den. Det er kanskje enklest å komme fram til utregningen om man regner baklengs. Mer om dette om prosessen TODO)
Et bevis kan bli til en ny regel#
Eksempel: 1. kvadratsetning

Vi kan bevise 1. kvadratsetning på måten vist til høyre. Vi tar utgangspunkt i en utregning som bruker kjente regler. Denne kan så forkortes til en ny regel.
Reglene vi startet med er på en måte “inni” den nye regelen. Vi kaller det noen ganger inni-regler. Noen ganger hender det at vi glemmer inni-regler og bare bruker den nye regelen; men helst bør en lærer kunne gå tilbake og forklare inni-reglene når det trengs.
Regel → bevis → regel#
Vi ser at bevis har regler inni seg (under: Tegnet mot venstre) og kan “bli til” nye bevis (under: tegnet mot høyre). Vi kan få kjeder av slike bevis, hvor de simpleste er lengst til venstre mens de mest konkrete er til høyre.
Forsøksvis(!) kan vi tegne opp dette slik:
Hva har vi så helt til venstre? Her kan vi ha
Aksiom (f.eks. Peanos aksiomer)
Handlinger i representasjonsspråk; men hvordan er så representasjonsspråkene utviklet?
“Bevistyper”#
Noen ganger snakker man om bevistyper; induksjonsbevis, indirekte bevis etc. Ellef mener det er mer fruktbart å snakke om bevis utifra hvilke regler de bruker. Bevistypene kan defineres slik:
Induksjonsbevis: Bruker induksjonsregelen
Indirekte bevis: Bruker en av de indirekte reglene
Direkte bevis: Bruker ikke en av de indirekte reglene
Uttømming-bevis: Bruker regelen om uttømming
Implikasjon og ekvivalens#
Argument og regler med ⇒ kalles implikasjon. Argument og regler med ⇔, som går begge veier, kalles ekvivalens. \(x = 2 ⇒ x^2 = 4\) er en implikasjon, men ikke en ekvivalens: Det finnes et tilfelle der \(x^2 = 4\) er sann (vi snakker om tilfellet at x er −2) men \(x = 2\) er usann, så det blir helt feil om noen påstår at \(x^2 = 4 ⇒ x = 2\).
Representasjoner#
Ord#
Premiss
Konklusjon
Formelspråket#
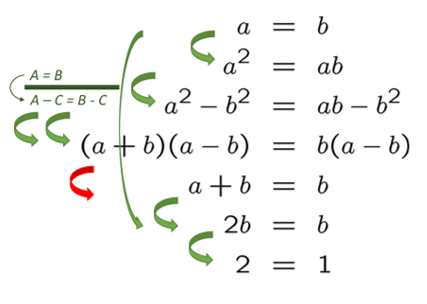
Fra før vet vi at påstander kan inneholde objekt med tegnet = mellom.
Argumenter kan inneholde påstander med tegnet ⇒ mellom. Andre tegn (som ⇔ ⇐) gir andre typer påstander.
Dette kan vi vise tydelig ved bokser. I følgende eksempel har vi tre nivå bokser: Den ytterste er et argument, den midterste to påstander og de innerste er fire objekt. Legg merke til at = setter sammen to objekt til en påstand og at ⇒ setter sammen to påstander til et argument.
\(\fbox{\(
\fbox{\(
\fbox{2 + \(x\)}\) = \(
\fbox{\(x^2\) - 4}
\)}
⇒
\fbox{\(
\fbox{2 + \(x\)} + 4\) = \(
\fbox{\(x^2\)}
\)}
\)}\)
I noen tradisjoner (Naturlig deduksjon, Gentzen) skriver man en argumentasjon eller regel med vannrett strek, f.eks. \(\frac{2 + x = x^2 - 4}{2 + x + 4 = x^2}\). Problemet med syntaksen er at den kan forveksles med brøk. Vi vil derfor heller velge å uttrykke tilsvarende med loddrett strek eller pil: \(\overset{2 + x = x^2 - 4}{\underset{2 + x + 4 = x^2}{↓}}\). Det kan også tenkes at vi vil uttrykke at argumentasjonen gjelder begge veier: \(\overset{2 + x = x^2 - 4}{\underset{2 + x + 4 = x^2}{⇵}}\)
I noen skolesammenhenger setter man to streker under konklusjonen. Det er mulig praksisen holder på å forsvinne siden den var enkel med teknologien “blyant og linjal” men vanskelig med en del digitale skriveprogram.
Bokser og piler#
Man kan representere påstander med for eksempel formelspråk og omskrivingene mellom dem med for eksempel piler som dem vi har brukt som regler. Pilenes retning er typisk mot høyre eller nedover. Da får man en representasjon som den til høyre.
Teknologier for bokser og piler#
Graphviz (som er brukt i de fleste slike diagram i Mashov).
Word Smart Art
PowerPoint
Papir og blyant, evt. sammen med mobilkamera
Algoritmer#
Evaluere bevis#
Finne om et bevis er sant.
Om vi snakker om en rekke påstander bundet sammen av regler kan vi i prinsippet sjekke alle regel-applikasjonene (alle overgangene mellom linjer). Har reglene forutsetninger vi må passe på?
Sjekk for eksempel følgende utregning:
\(a = b\) (forutsetning) \(a^2 = ab\) (ganger med \(a\) på begge sider \(a^2 - b^2 = ab - b^2\) (trekker fra \(b^2\) på begge sider) \((a + b)(a - b) = b(a - b)\) (faktoriserer, konjugatsetningen og distributivitet) \(a + b = b\) (deler på \((a - b)\) på begge sider i likningen) \(b + b = b\) (siden vi har forutsatt \(a = b\) kan vi sette inn \(\{a ↦ b\}\)) \(2 = 1\) (deler på \(b\) på begge sider)
Vi har altså bevist at \(2 = 1\). Det er jo mildt sagt overraskende og slår beina vekk under det meste av det vi holder på med. Hva er feil?
Løsningsforslag
Heldigvis kan vi avsløre feilen. Den ligger i linja der vi deler på \(a-b\) på begge sider. Siden \(a = b\) er nemlig \(a - b\) lik 0. Vi kan ikke dele på 0 på begge sider. Det må vi alltid passe på når vi deler på begge sider!
Finne / lage bevis#
Dette er mye vanskeligere! Vi snakker mer om dette under prosess, som er neste kolonne.
Vi har en del standard triks om problemløsing, bl.a. fra Polya. Noen av dem er:
Bruk eksempler først
Representer alt du vet, både om premissene og svaret
Arbeid både fra premissene og fra konklusjonen (“overfra og nedenfra”)
Som lærere er det vel sjelden vi får i oppgave å lage “store” bevis. Men det er vanlig at vi må “bevise” vanlige regler. Noen bevis kan man huske, men man bør også kunne lage noen nye.
Når elevene lager utregninger bruker de også mange av de samme teknikkene.
Oppgaver#
TODO flytte?
Oppgave: Bevis at 2 + 3 = 5.
Oppgave: Bevis at summen av to oddetall alltid er et partall.
Bevis at \(∀(n + 1) = p^2 + q^2\)
Oppgave: “Bevis at ethvert oddetall kan skrives som en sum av to kvadrattall”.
Hva er objektene? Hvordan kan de representeres?
Hva er påstanden du skal bevise?
Forsøk å lage et bevis, og observer prosessen. Om dere er en gruppe kan tre stk lage bevis og én observere. Legg for eksempel merke til om dere beviser fra premisset til konklusjon eller om dere beviser baklengs.
Løfte elever til regelbasert deduksjon#
Aspekt#
Argumentet \(x - 1 = 2 ⇒ x = 2 + 1\) kan forståes på flere måter:
En påstand om at om premisset \(x - 1 = 2\) er sann må konklusjonen \(x = 2 + 1\) være sann.
I alle verdener hvor premisset \(x - 1 = 2\) er sann må konklusjonen \(x = 2 + 1\) være sann.
Mengden av alle verdener hvor premisset \(x - 1 = 2\) er sann er delmengde \(⊂\) av alle verdener hvor konklusjonen \(x = 2 + 1\) er sann.
En regel / redskap. Om vi tilfeldigvis vet at premisset er sant kan vi bruke regelen til å påstå at konklusjonen er sann.
En mulig omskriving: Vi kan skrive om \(x - 1 = 2\) til \(x = 2 + 1\): \(\overset{x - 1 = 2}{\underset{x = 2 + 1}{↓}}\).
Læring#
Tilsvarer sannsynligvis viktige måter å generalisere på.
Datatyper#
Skissemessig, dette er muligens utenfor MA302; men Ellef synes det er interessant!
Objekt:
1, 2, 3: ℕ
¼, ⅓, ½: ℚ
π, e, √2: ℝ
+, −, ×, ÷: ℝ × ℝ → ℝ (altså: de tar to reelle tall som argument og gir et nytt reelt tall)
√: ℝ > 0 → ℝ
Påstander:
=, <, ≠: ℝ × ℝ → 𝔹 (altså: de tar to reelle tall som argument og gir en sannhetsverdi)
∧, ∨: 𝔹 × 𝔹 → 𝔹 (∧ betyr og, ∨ betyr eller)
¬: 𝔹 → 𝔹
Argument:
⇒, ⇔: 𝔹 × 𝔹 → 𝔹
Objekt er typisk av typene ℕ eller ℝ. Påstander (sannhetsverdier) er sanne eller usanne — typen 𝔹?
