÷ Dividere brøker

Forutsetninger og læringsmål

Læringsmål

Du skal dividere to brøker

Introduksjon

Divisjon

Hva er ⅔÷⅕?

Slike regnestykker kan oppleves vanskelig. Man kan oppleve om målet er at elever skal forstå dette ordentlig, om de bare skal ha en formel de kan bruke til å løse regnestykker eller om de ikke trenger å mestre slike regnestykker. Uansett er det nødvendig å være stø på en hel del inni-algoritmer (blant annet multiplikasjon) før eleven (og du) begynner med dette.

Representasjoner

Regnefortellinger

Bruker vi delingsdivisjon, kan det være vanskelig å finne regnefortellinger for dette. Om vi bruker målingsdivisjon, derimot, går det greiere: Du har to tredels liter julebrus. Det skal fordeles på flasker som tar ⅕ liter. Hvor mange flasker? Vi aner kanskje at svaret må være rundt tre flasker, og kan sjekke det ved å observere at tre flasker tar 3/5 liter.

Utregning i flisalgoritmen

Divisjonsalgoritmene vi har brukt tidligere fungerer fortsatt. Riktignok mener noe at de følgende representasjonene er vanskelig å forstå.

Med målingsdivisjon av 2/15 og 2/3 plasserer vi dividend og divisor til venstre, så kommer kvotienten ut til høyre: .
Skal vi dele 2/3 på 1/5, blir altså julebrusen plassert øverst til venstre, og skal fordeles på en flaske som er nederst til venstre. Brusen blir “skvist” oppover i en trang søyle: 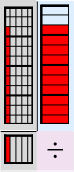. “Oppover” betyr nå “antall flasker”. Svaret kommer ut til høyre: Ti tredeler. Dividend-området øverst til venstre inneholder nå ti femten-deler: Hvorfor det?

Med delingsdivisjon av 2/15 og 2/3 plasserer vi dividend og divisor øverst, så kommer kvotienten ut nederst: .
Skal vi dele 2/3 på 1/5 blir de 2/3 nå skvist bortover: 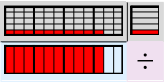. Svaret ser vi nederst.

Utregning i formler

Divisjonsstykker som \(\frac{2}{3} ÷ \frac{4}{5}\) kan oppleves vanskelig. Vi skal bruke et triks: Om vi har et divisjonsstykke a÷b, kan vi multiplisere både dividend og divisor med samme tall. Dette er omtrent det samme som å “splitte” brøken a/b med n. Vi skal nå multiplisere både \(\frac{2}{3}\) og \(\frac{1}{5}\) med den omvendte brøken av den siste (altså \(\frac{5}{4}\)): Da vår vi \(\frac{5·2}{4·3} ÷ \frac{5·4}{4·5}\) som blir \(\frac{5·2}{4·3} ÷ \frac{20}{20}\) og \(\frac{5·2}{4·3} ÷ \textbf{1}\) og \(\frac{5·2}{4·3}\). Med dette trikset blir vi kvitt deletegnet, og divisoren blir kastet inn til divisoren opp ned!

Dette kan vi gjøre med alle brøker. Vi har at \(\overset{r\frac{a}{b}÷\frac{c}{d}}{\underset{r\frac{a}{b}·\frac{d}{c}}{↓}}\) eller mer generelt \(\overset{re÷\frac{c}{d}}{\underset{re·\frac{d}{c}}{↓}}\). Å pugge og bruke denne formelen er egentlig ganske lett, men om den introduseres for tidlig gir den lett forståelse som er basert på løsrevne regler og ikke representasjoner

Ord

Formelspråk

Småstein og fliser

Algoritmer

Utifra representasjoner

Alle over gir opphav til algoritmer. Men lite praksis? Unntak følger:

Regnefortellinger

Liter delt på halvlitersflasker

Formel: Snu den siste

Didaktikk

Formel. INstrumentell. FJernet fra forståelse. Lærer at de tikke kan forståes.

Er nå dette så viktig?