= Like brøker#
Forutsetninger og læringsmål#
Du skal kunne
Avgjøre om to brøker er like.
Introduksjon#
Wiggo har fire roser 🌹🌹🌹🌹 han skal dele i seks buketter
 . Hvor mange roser blir det i hver bukett?
. Hvor mange roser blir det i hver bukett?
Svaret kan bli  (altså \(\frac{4}{6}\)); men om vi ser etter, ser vi at svaret må bli det samme som da han skulle dele to roser på 🌹🌹 på tre buketter
(altså \(\frac{4}{6}\)); men om vi ser etter, ser vi at svaret må bli det samme som da han skulle dele to roser på 🌹🌹 på tre buketter  , altså
, altså  (altså \(\frac{2}{3}\)); han kan jo bare fordele først to roser på de første tre bukettene og så de to siste på de siste tre bukettene. De to brøkene har altså samme verdi: \(\frac{4}{6} = \frac{2}{3}\).
(altså \(\frac{2}{3}\)); han kan jo bare fordele først to roser på de første tre bukettene og så de to siste på de siste tre bukettene. De to brøkene har altså samme verdi: \(\frac{4}{6} = \frac{2}{3}\).
Det er vanlig å si at  er lik
er lik  . Verdien er jo lik, og brøkene er samme sted på tall-linja. Samtidig er det klart at for elever og matematikere er brøkene to ulike matematiske objekt. Det er for eksempel mulig å vite verdien av \(\frac{2}{3}\) uten å vite verdien av \(\frac{4}{6}\). Lærere må være klar over at for elever er det ikke selvfølgelig at brøkene er “like”; de er ikke samme brøk, selv om de har lik verdi!
. Verdien er jo lik, og brøkene er samme sted på tall-linja. Samtidig er det klart at for elever og matematikere er brøkene to ulike matematiske objekt. Det er for eksempel mulig å vite verdien av \(\frac{2}{3}\) uten å vite verdien av \(\frac{4}{6}\). Lærere må være klar over at for elever er det ikke selvfølgelig at brøkene er “like”; de er ikke samme brøk, selv om de har lik verdi!
Nedenfor skal vi drøfte mer filosofiske spørsmål om likhet og identitet.
https://phet.colorado.edu/en/simulations/fraction-matcherRepresentasjoner#
Ord#
I praksis sier vi at to brøker er like. Noen foretrekker å si at de har lik verdi eller er likeverdige, men det blir fort for klumsete i praksis.
Formelspråk#
Det kan være vanskelig å avgjøre utifra en formel om to brøker er like. Er \(\frac{7}{22}\) lik \(\frac{8}{25}\)? Om vi bruker litt tid på dette må det være enda vanskeligere for en elev.
Steinbit#
I steinbitspråket er det også rimelig at
 er lik
er lik
 .
.
Bløtkake#
I bløtkakespråket er det rimelig at
 er lik
er lik
 .
.
Tall-linja#
Også på tall-linja er fire av seks hopp
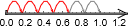 det samme som
det samme som
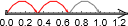 .
.
Algoritmer#
Å se på en representasjon#
TODO
I praksis er det ofte greit å se på en representasjon.
Noen ganger unøyaktig.
Greit å lage representasjon. Skrive tall på en tall-linje (f.eks. GeoGebra). Teknologi for å lage representasjoner.
Skrive på felles brøkstrek#
Senere skal vi lære å splitte og samle brøker så de får felles brøkstrek.
Regne til desimaltall#
Vi kan også regne til desimaltall TODO
Dette er også nyttig for å lære elevene å se sammenhengen mellom brøk og desimaltall.
Sammenlikne med heltall og desimaltall#
Algoritmene over kan også brukes til å sammenlikne en brøk med heltall og desimaltall.
Og man kan alltid regne et heltall og desimaltall om til brøk først, og sammenlikne det.
Læring#
Filosofi#
Identiteter#
Her følger noen spørsmål vi ikke er sikre på.
Er ½ det samme som 0.5?#
Klart: Verdien er lik
Klart: Pedagogisk ulikt.
Er ⅔ det samme som 2÷3?#
Verdien er
Er \(\frac{2}{3}\) det samme som \(\frac{4}{6}\)?#
Det er vanlig å si at de er like. Det har vi også gjort over.
Samtidig er det klart at de er to konsepter.
Filosofisk om de er samme?
