Flere kategoriske parametre#
Forutsetninger og læringsmål#
Flere parametre. En serie.
Mengder og sannsynlighet QED 7.6s790
Representasjon
Tabell, hisogram, is
Introduksjon#
Referanser#
Kombinatorikk (Klaveness et al, 2019) 42s242
Eksempler#
Terning#
Mynt#
Is#
<🔴🔵🟢
Begrep#
Ordnet (permutasjon) og uordnet (kombinasjon#
Er isen <🔴🔵 forskjellig fra <🔵🔴?
Om <🔴🔵 regnes som forskjellig fra <🔵🔴, sier vi at vi har ordnet utvalg (permutasjon). Vi burde kanskje ikke si at “utvalget er ordnet”, men at “ordningen betyr noe” i utvalget. Men i tradisjonell ordbruk sier vi altå at utvalget er ordnet om rekkefølgen betyr noe, og uordnet om rekkefølgen ikke betyr noe.
Når vi kaster to terninger og summerer svarene, betyr rekkefølgen ikke noe; da har vi uordnet utvalg (kombinasjon).
Rekkefølger QEDStning13 s818
Med og uten repetisjon / tilbakelegging#
Kan man velge samme kule to ganger? Altså: Er <🟢🟢 en mulig is?
https://www.matematikk.org/artikkel.html?tid=154542&within_tid=154366
Representasjoner#
Ord#
Utfallstre Valgtre#
https://www.matematikk.org/artikkel.html?tid=154554&within_tid=154366
Småstein og fliser#
Algoritmer#
Lover 1#
Multiplikasjonsloven utvidet#
Multiplikasjonsloven utvidet QED Setning 12 s816.
Lover 2: Utvalgstypene#
Undervisningsopplegg: https://www.matematikk.org/uopplegg.html?tid=105780
Ordnet utvalg med tilbakelegging#
QED 7.8.2 s822
\(n^k\).
Eksempel: Tippekupongen; 12 kamper med 3 muligheter hver (H, U,B): \(12^3\)
Eksempel is: Av tekniske grunner skrives 🔵 som ‘b’, 🔴 som ‘r’ og 🟢 som ‘g’.
\(n\) blir her antall kuler (nivå i treet), mens \(k\) er antall valgmuligheter i hvert nivå.
graphvizSource("""digraph G{
compound=true;
rankdir=TB
ranksep="0.3"
nodesep="0.01"
pad=0
node[shape="plaintext"]
edge [fontsize=10]
start [label="Start" ]
start -> b [color=blue]
start -> r [color=red]
start -> g [color=green]
b -> bb [color=blue]
b -> br [color=red]
b -> bg [color=green]
r -> rb [color=blue]
r -> rr [color=red]
r -> rg [color=green]
g -> gb [color=blue]
g -> gr [color=red]
g -> gg [color=green]
bb -> bbb [color=blue]
bb -> bbr [color=red]
bb -> bbg [color=green]
br -> brb [color=blue]
br -> brr [color=red]
br -> brg [color=green]
bg -> bgb [color=blue]
bg -> bgr [color=red]
bg -> bgg [color=green]
rb -> rbb [color=blue]
rb -> rbr [color=red]
rb -> rbg [color=green]
rr -> rrb [color=blue]
rr -> rrr [color=red]
rr -> rrg [color=green]
rg -> rgb [color=blue]
rg -> rgr [color=red]
rg -> rgg [color=green]
gb -> gbb [color=blue]
gb -> gbr [color=red]
gb -> gbg [color=green]
gr -> grb [color=blue]
gr -> grr [color=red]
gr -> grg [color=green]
gg -> ggb [color=blue]
gg -> ggr [color=red]
gg -> ggg [color=green]
}""")
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[1], line 1
----> 1 graphvizSource("""digraph G{
2 compound=true;
3 rankdir=TB
4 ranksep="0.3"
5 nodesep="0.01"
6 pad=0
7 node[shape="plaintext"]
8 edge [fontsize=10]
9 start [label="Start" ]
10 start -> b [color=blue]
11 start -> r [color=red]
12 start -> g [color=green]
13 b -> bb [color=blue]
14 b -> br [color=red]
15 b -> bg [color=green]
16 r -> rb [color=blue]
17 r -> rr [color=red]
18 r -> rg [color=green]
19 g -> gb [color=blue]
20 g -> gr [color=red]
21 g -> gg [color=green]
22 bb -> bbb [color=blue]
23 bb -> bbr [color=red]
24 bb -> bbg [color=green]
25 br -> brb [color=blue]
26 br -> brr [color=red]
27 br -> brg [color=green]
28 bg -> bgb [color=blue]
29 bg -> bgr [color=red]
30 bg -> bgg [color=green]
31 rb -> rbb [color=blue]
32 rb -> rbr [color=red]
33 rb -> rbg [color=green]
34 rr -> rrb [color=blue]
35 rr -> rrr [color=red]
36 rr -> rrg [color=green]
37 rg -> rgb [color=blue]
38 rg -> rgr [color=red]
39 rg -> rgg [color=green]
40 gb -> gbb [color=blue]
41 gb -> gbr [color=red]
42 gb -> gbg [color=green]
43 gr -> grb [color=blue]
44 gr -> grr [color=red]
45 gr -> grg [color=green]
46 gg -> ggb [color=blue]
47 gg -> ggr [color=red]
48 gg -> ggg [color=green]
49 }""")
NameError: name 'graphvizSource' is not defined
Ordnet utvalg uten tilbakelegging#
QED 7.8.3 s825
\(\frac{n!}{(n-k)!} = n \text{P} k\)
Eksempel: Urne med baller: Rekkefølgen er vesentlig, man legger ikke tilbake.
I iseksempelet blir da noen veier forbudte:
graphvizSource("""digraph G{
compound=true;
rankdir=TB
ranksep="0.3"
nodesep="0.01"
pad=0
node[shape="plaintext"]
edge [fontsize=10]
start [label="Start" ]
{node [fontcolor=lightgray];
bb bbb bbr bbg
brr brb
bgg bgb
rbb rbr
rr rrb rrr rrg
rgg rgr
gbb gbg
grr grg
gg ggb ggr ggg
}
start -> b [color=blue]
start -> r [color=red]
start -> g [color=green]
b -> bb [color=blue style=dotted]
b -> br [color=red]
b -> bg [color=green]
r -> rb [color=blue]
r -> rr [color=red style=dotted]
r -> rg [color=green]
g -> gb [color=blue]
g -> gr [color=red]
g -> gg [color=green style=dotted]
bb -> bbb [color=blue style=dotted]
bb -> bbr [color=red]
bb -> bbg [color=green]
br -> brb [color=blue style=dotted]
br -> brr [color=red style=dotted]
br -> brg [color=green]
bg -> bgb [color=blue style=dotted]
bg -> bgr [color=red]
bg -> bgg [color=green style=dotted]
rb -> rbb [color=blue style=dotted]
rb -> rbr [color=red style=dotted]
rb -> rbg [color=green]
rr -> rrb [color=blue]
rr -> rrr [color=red style=dotted]
rr -> rrg [color=green]
rg -> rgb [color=blue]
rg -> rgr [color=red style=dotted]
rg -> rgg [color=green style=dotted]
gb -> gbb [color=blue style=dotted]
gb -> gbr [color=red]
gb -> gbg [color=green style=dotted]
gr -> grb [color=blue]
gr -> grr [color=red style=dotted]
gr -> grg [color=green style=dotted]
gg -> ggb [color=blue]
gg -> ggr [color=red]
gg -> ggg [color=green style=dotted]
}""")

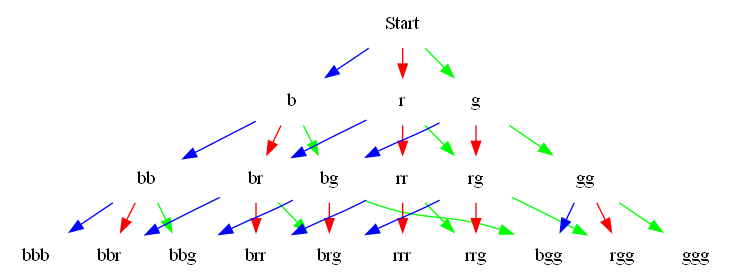
Uordnet utvalg med tilbakelegging#
Binomialkoeffisienten
\({n\choose k}\) = \({n!} \over {k!(n - k)!}\) = \(n\text{C}k\)
Eksempel: Lotto
graphvizSource("""digraph G{
compound=true;
rankdir=TB
ranksep="0.3"
nodesep="0.01"
pad=0
node[shape="plaintext"]
edge [fontsize=10]
start [label="Start" ]
start -> b [color=blue]
start -> r [color=red]
start -> g [color=green]
b -> bb [color=blue]
b -> br [color=red]
b -> bg [color=green]
r -> br [color=blue]
r -> rr [color=red]
r -> rg [color=green]
g -> bg [color=blue]
g -> rg [color=red]
g -> gg [color=green]
bb -> bbb [color=blue]
bb -> bbr [color=red]
bb -> bbg [color=green]
br -> bbr [color=blue]
br -> brr [color=red]
br -> brg [color=green]
bg -> bbg [color=blue]
bg -> brg [color=red]
bg -> bgg [color=green]
rr -> brr [color=blue]
rr -> rrr [color=red]
rr -> rrg [color=green]
rg -> brg [color=blue]
rg -> rrg [color=red]
rg -> rgg [color=green]
gg -> bgg [color=blue]
gg -> rgg [color=red]
gg -> ggg [color=green]
}""")
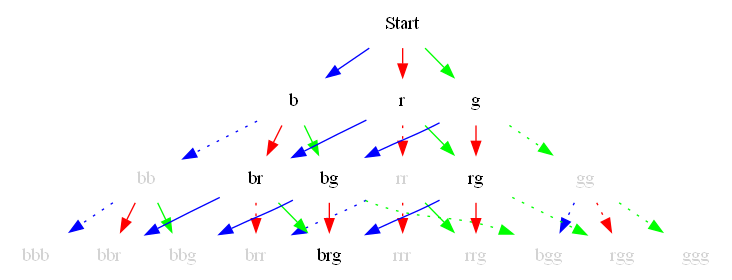
Uordnet utvalg uten tilbakelegging#
\({(n + k - 1)!} \over {k!(n - 1)!}\) = \({n + k - 1} \choose {k}\) = \({n + k - 1} \choose {n - 1}\)
QED 7.8.3 s828
graphvizSource("""digraph G{
compound=true;
rankdir=TB
ranksep="0.3"
nodesep="0.01"
pad=0
node[shape="plaintext"]
edge [fontsize=10]
{node [fontcolor=lightgray];
bb rr gg
bbb bbr bbg brr rrr rrg bgg rgg ggg
}
start [label="Start" ]
start -> b [color=blue]
start -> r [color=red]
start -> g [color=green]
b -> bb [color=blue style=dotted]
b -> br [color=red]
b -> bg [color=green]
r -> br [color=blue]
r -> rr [color=red style=dotted]
r -> rg [color=green]
g -> bg [color=blue]
g -> rg [color=red]
g -> gg [color=green style=dotted]
bb -> bbb [color=blue style=dotted]
bb -> bbr [color=red]
bb -> bbg [color=green]
br -> bbr [color=blue]
br -> brr [color=red style=dotted]
br -> brg [color=green]
bg -> bbg [color=blue]
bg -> brg [color=red]
bg -> bgg [color=green style=dotted]
rr -> brr [color=blue style=dotted]
rr -> rrr [color=red style=dotted]
rr -> rrg [color=green]
rg -> brg [color=blue]
rg -> rrg [color=red]
rg -> rgg [color=green style=dotted]
gg -> bgg [color=blue style=dotted]
gg -> rgg [color=red style=dotted]
gg -> ggg [color=green style=dotted]
}""")
Lover 3#
Binomisk sannsynlighetsfordeling#
QED 7.9 834
Hypergeometrisk sannsynlighetsfordeling#
QED 7.10 s839
