1.4.4. Likning#
Forutsetninger og læringsmål#
Vi skal nå introdusere likninger. Likningen er den vanligste formen for utsagn i skolematematikken.
Likninger bygger på forståelse av parenteser, matematiske skrivemåter (som \(ab\) og \(23\)) algebra (blant annet variabelbegrepet og bokstavuttrykk). Vi forutsetter også god kjennskap til addisjon, multiplikasjon og enkel potensregning (du må vite hva x^2, x^1, x^0 og x^-1 er).
Likninger vil bli brukt videre i mye annen matematikk.
Det finnes mange typer likninger, og det er et kraftig verktøy som brukes i mye matematikk. Det er svært nyttig å kunne både repesentasjoner og algoritmer!
Denne sida handler om likninger; for å begrense sidestørrelsen er regler for likninger og løsing av likninger skilt ut som egne sider.
Likninger er eksempel på påstander, som blir behandlet mer generelt under argumentasjon. Likningsregler er eksempel på regler om påstander. Likningsløsing er eksempel på bevis.
Oppgaver#
(Klaveness et al, 2019) 75 Likningstegnet betyr lik verdi
(Klaveness et al, 2019) 88s334 Likninger med fyrstikker
Læreplan #
Annet#
(Hinna et al, 2016) s323
Introduksjon#
Et tall minus to er lik tre. Hvilket tall?
Kathrine påstår at \(x^2 + 2x\) er lik \(2x + 4\). Hvilken verdi må settes inn i \(x\) for at Kathrine skal ha rett?
Grunnidéen i likninger ligger i navnet: Vi har to ting som er like. De to “tingene” kan være bokstavuttrykk, og vi kaller dem venstre og høyre side.
En likning er typisk laget sånn at den har en bundet variabel (f.eks. \(x\)); bare noen verdier i \(x\) gjør venstre- og høyresidene like (så likningen blir sann). I likningen \(x - 2 = 3\) gjør verdien \(5\) at likningen blir sann.
Representasjoner#
Ord#
De to uttrykkene som er lik hverandre kalles vanligvis for venstreside og høyreside.
Man kan skille mellom
“løsningen” av en likningen (argumentasjonene; utregningen som fører fram til et svar)
“løsingen”; prosessen med å lage en løsning.
Svaret på en likning er en innsetting, for eksempel {x ↦ 3}. De fleste skriver bare at “x = 3” er løsningen, men i Mashov vil vi skille mellom de to og bruke innsetting for å skrive svaret.
Balansevekt#

En beslektet representasjon er dumphuske.
Inni-representasjoner#
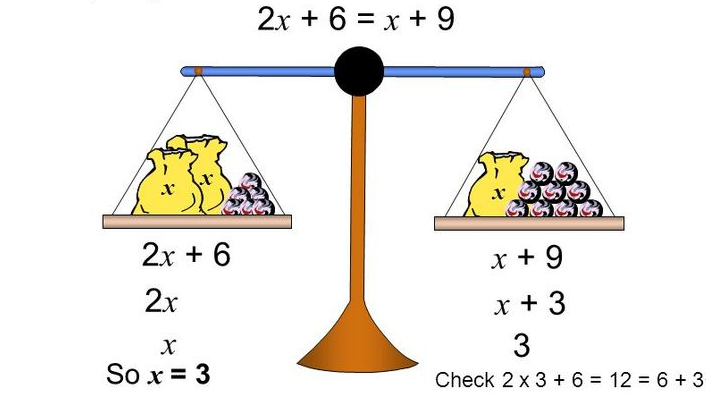
Om vi representerer likning-konstruksjonen som en balansevekt representerer vi venstre- og høyresidene i hver sin skål. De må også representeres, og det kan gjøres på alle de vanlige måtene. Vi kan skrive sidene som formler (som over: \(x + 3\) og \(5\)), men vi kan også bruke fyrstikkesker, formler eller andre ting. I tegningen til høyre er \(x\) representert ved melposer.
Teknikk#
I klasserommet kan det være egnet å bruke en planke som balanserer. Elevene skjønner jo poenget raskt, så snart kan man bruke enklere versjoner, for eksempel å to hauger på hver sin side av bordet.
Ellef kjenner ikke gode dataprogram for å automatisk tegne skålvekter; men i mange tilfeller kan det være et alternativ å tegne en med penn og papir, og så ta bilde med mobiltelefonen. Snart kan man nok lage slike tegninger med automatisk bildegenerering.
En del interaktiviteter finnes i Phet.
https://teacher.desmos.com/activitybuilder/custom/5b92e7a407624d32bf1bf88a
https://solveme.edc.org/ → Mobiles
Formelspråk#
Likhetstegnet#
I likninger er det tydelig at likhetstegnet = betyr “er lik”. Elever som oppfatter = som “nå kommer svaret” eller “kan skrives om til” kan få problemer med å skjønne at = betyr “er lik”. = er symmetrisk og gir en sannhetsverdi.
I Mashov brukes = bare for “er lik”. Menes “kan skrives om til” brukes →. Senere skal vi bruke tegnet ↦ (som i \(x ↦ 5\)) for løsningen av en likning.
Likning#
Formelspråket er i grunn veldig enkelt: Vi skriver først en representasjon for det ene (venstresiden), så et likhetstegn (\(=\)), så en representasjon for det andre som skal være likt (høyresiden). Eksempel er \(x + 2 = 3\).
Det er også vanlig å skrive \(A = B = C\). Det blir jo forstått (som \(A = B ∧ B = C\)), men har formelle problemer.
Vanligvis, når vi bruker likhetstegn, skriver vi også venstre- og høyresiden som formler. Men vi kan også bruke inni-representasjoner av andre språk. Vi kan for eksempel bruke konvolutter for variabel og eplespråket for tall, og skrive ✉ + 🍎🍎 = 🍎🍎🍎 .
Programmeringsspråk#
I mange programmeringsspråk, inkludert Python, brukes to likhetstegn == for er lik, mens ett = brukes for settes lik. Uttrykket x == 2 er altså True hviss x har verdien 2; utrykket x = 2 gjør altså at x får verdien 2. I if-setninger skal vi altså vanligvis bruke to likhetstegn.
Rektangler#
Det hender vi tegner opp venstre- og høyresidene som bokser: \(\fbox{x + 2} \fbox{3}\). Det hender vi spanderer både en boks og et likhetstegn: \(\fbox{x + 2}=\fbox{3}\) for ekstra tydelighet.
Koordinatsystem#
Dette forutsetter kunnskap om koordinatsystem og funksjoner:
Vi kan tegne opp venstre- og høyresidene som to funksjoner i samme koordinatsystem. Når funksjonene treffer hverandre er altså venstresiden like stor som høyresiden; her er løsningen på likningen. Løsningen er altså x-verdiene der sidene har lik verdi. Dette er altså de x-verdiene hvor venstre- og høyrekurvene er like høye på y-aksen.
Her er et eksempel for likningen \(2x + 3 = x^2 - 5\):
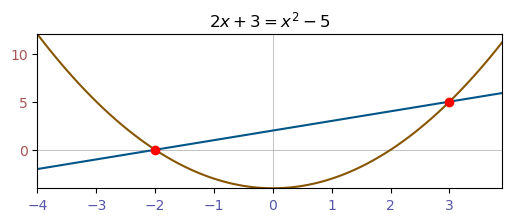
Denne representasjonen
gir innsikt i hva en venstre- og høyreside er
er nyttig i algoritmen grafisk løsning
vil bli nyttig senere.
Et spesielt eksempel er om en av sidene er konstant (f.eks. \(2x = 4\)). Hvordan ser linjene ut da?
Likninger i GeoGebra#

Om man skriver en likning (f.eks. 2x + 2 = 8) inn i GeoGebra, får man bare en loddrett strek ved løsningen (x er 3). Det kan synes overraskende; det skyldes at GeoGebra forenkler (i praksis: løser) likningen før den tegnes opp.
Skal vi tegne likningen ‘uforenklet’, må vi tegne hver side for seg. Vi kan for eksempel skrive venstre(x) = 2x + 2, høyre(x) = 8 og tilmed løsning = Intersect(venstre, høyre).

Algoritmer#
Modellere: Lage likning fra en virkelig situasjon#
Modellere fra virkeligheten.
Modellering er jo et kjerneelement i LK20.
Oversette fra en representasjon til en annen#
For eksempel oversette
Fra virkelig situasjon (regnefortelling) til skålvekt
Fra skålvekt til formel
Fra formel til koordinatsystem
Løse likning#
Man kan finne en løsning ved å bruke forskjellige strategier (som vi vil komme tilbake til), for eksempel ved regler for likninger. Dette er så mye tekst at det er skilt ut til egne sider.
Aspekter ved likninger#
En likning (f.eks. \(x - 2 = 3\)) kan sees på flere måter:
Et utsagn som er sant#
Setningen “x minus to er lik 3” er et utsagn som er sant eller ikke. Det spesielle her er at det er sant for én verdi av x og usant om andre.
Det finnes andre typer utsagn enn likninger. Eksempler er ulikheter som \(x < 3\) og \(x ≠ 3\) (som begge er sanne for noen x og usanne for andre).
Hvilke x-er utsagnet er sant for (løsningsmengde)#
Vi kan også snakke om hvilke verdier for x som gjør utsagnet sant. Mengden av disse verdiene kalles løsningsmengden.
I noen overganger mellom likninger har vi en implikasjon som bare går én vei. Eksempel:
1: \(x = 2\) Løsnngsmengden er \({2}\)
⇓ Implikasjon, men ikke ekvivalens
2: \(x^2 = 4\) Løsningsmengden her er større! \({−2, 2}\)
Typer av likninger#
Her følger noen likningstyper. Her gir vi bare oversikt; detaljene kan komme i egne dokumenter .
Det er vanlig å begynne med enkle. Men kan miste oversikten. Det finnes fordeler ved å begynne på mer virkelighetsnære likninger.
Førstegrad#
Førstegradslikninger kan skrives på formen \(ax + b = 0\). De kalles førstegradslikninger fordi de inneholder x¹.
I koordinatsystem-representasjonen vil likninger på denne formen framstå som rette linjer.
Vi kan regne ut det generelle tilfellet at om det er sant at \(ax + b = 0\) må det være sant at \(x = −b/a\). Utregningen / beviset er ganske enkelt. Dette resultatet kan vi putte i formelbiblioteket vårt.
Vi skal snakke mer om dette når vi kommer til førstegradsfunksjoner.
Andre grad#
Andregradslikninger kan skrives på formen \(ax² + bx + c = 0\). De kalles andregradslikninger fordi de inneholder x².
I koordinatsystem-representasjonen vil likninger på denne formen framstå som parabler. Om a er positiv vil parabelen “smile”, altså vokse til sidene og ha et bunnpunkt. Da (når me kan seie at a veks til sidan) sier vi at den er konveks. Om a er negativ (og er sur) sier vi at den er konkav.
Vi kan (ved hjelp av bl.a. kvadratkomplettering udl.no) regne ut en generell formel for også slike likninger.
ndla.no om andregradslikninger
Vi skal snakke mer om dette når vi kommer til andregradsfunksjoner.
Diofantinske likninger#
Diofantinske likninger er likninger hvor variabelen bare har heltallige løsninger. Vi skal ikke bruke alt for mye tid på dette.
Læring#
Læring av likninger kan bli oppfattet som vanskelige. Mange henfaller til instrumentell bruk av regler.
Det som vanlig viktig å ha gode representasjoner samtidig som man bygger algoritmer/oppskrifter/ferdigheter.
Om elever må lære seg variabelbegrepet, regneregler i aritmetikk i andre ting samtidig som de lærer likninger blir det mye å lære på en gang. Man bør ha en progresjon som gir passe læringsmengde om gangen.
Talltyper#
Bool (sannhetsverdier)#
Utsagn kan være sanne eller usanne. Sannhetsverdier er en ny datatype. Det finnes (i utgangspunktet) bare to verdier i denne datatypen: Sann og Usann. Noen kaller denne datatypen “boolsk” og bruker symbolet 𝔹.
Noen ganger snakker vi også om en verdi “Vet ikke”.
Operatoren + tar to reelle tall (eller “reelt bokstavuttrykk”) og gir et reelt tall (eller tilsvarende uttrykk). Operatoren = tar også to reelle tall eller uttrykk (kalt venstre- og høyreside), og gir en sannhetsverdi: sant eller usant.
