Pluss

1.1.6. Pluss#

Forutsetninger og læringsmål#

Du skal kunne

lese addisjon i tellbar mengde-språket
addere forskjellige typer stykker med forskjellige addisjoner, og se sammenhengen mellom dem

Kart#

Vi kan tegne opp et kart slik:

Hensikt#

For voksne er det neppe nødvendig å argumentere for at addisjon er viktig i dagliglivet. For barn, i alderen de lærer addisjon, er det neppe nødvendig å argumentere for noe som helst.

Likevel kan det for didaktikere være nyttig å sette ord på hvorfor addisjon er viktig å kunne. Disse ordene kan senere hjelpe oss å forstå hvorfor annen kunnskap er nyttig (eller ikke nyttig). Kanskje addisjon er viktig

Fordi det modellerer mange situasjoner i verden
Fordi mange algoritmer (oppskrifter) kan løse mange praktiske problem; addisjon opptrer generelt
Fordi læreplanen sier vi skal lære addisjon
Fordi addisjon er grunnlag for mye annen matematikk
Om matematisk kunnskap har en egenverdi uavhengig av nytte vil mange si at addisjon er sentralt.

Introduksjon: Grønne og blå#

Vi har to grønne steiner og tre blå. Hvor mange har vi til sammen?

Svaret er .

Representasjoner#

Hvordan kan vi representere denne situasjonen, og addisjon, i forskjellige representasjoner?

Småstein#

Vi kan sette ved siden av . Vi får da , altså . Fargene er ikke nødvendige, men hjelper oss å holde styr på hva som er hva.

Litt mer formelt: I tellbar mengde-språkene (hvor det som skal telles er sjokolader, epler, småstein, røde firkanter eller noe annet) kan vi sette en representasjon av den ene addenden (det ene som skal adderes) ved siden av en representasjon for den andre.

Noen ganger velger vi å sette tegnet “+” mellom tallene: +. Dette er nyttig når vi bare bruker én farge, for å få fram at er noe annet enn .

har selvfølgelig lik verdi som i den forstand at antallet (antall sjokolader, småstein eller røde firkanter) er det samme i dem. representerer likevel et annet objekt enn . Både matematikere og barn tenker på dem som to forskjellige ting.

Konkreter#

Konkreter er fysiske ting som likner på representasjonsspråk. Eksempel er fysiske småstein, fysiske epler eller andre ting. Dette er en svært gammel teknologi. Den har stor plass i undervisningen på lave årstrinn; et mål med Mashov er å bruke liknende språk også i høyere årstrinn.

Formelspråket#

I formelspråket bruker vi tegnet +; vi skriver 2 + 3, med +tegnet operandene (det vi skal legge sammen).

Barn som er vant til skrivemåten uten plusstegn kan komme til å prøve noe liknende med sifre; de skriver kanskje “23” når de mener “2 + 3”. Det går ikke, siden “23” i vårt tallsystem betyr noe helt annet.

Ord#

Det vi har beskrevet kaller vi å legge sammen, pluss, addisjon eller å legge til. Vi kan si ting som “to pluss tre” eller “å legge sammen to og tre”.

For barn er det i utgangspunktet ikke en selvfølge at disse ordene betyr det samme, og at de betyr det vi har beskrevet over.

Barn bruker også ordet “og”. Matematikere har en tendens til å mislike dette, siden ordet “og” også betyr andre ting (mengde-union og boolsk og). Men hvorfor skal noen få matematikere bestemme hva som er riktig mer enn hundre tusen barn?

Vi må riktignok være bevisst på å skille mellom å legge sammen to mengder (union) og legge sammen antallet av to mengder (addisjon).

Det som skal legges sammen kalles addender; dette er neppe vanlig ord for elever, men vil bli brukt i dette dokumentet. Det som er lagt sammen kalles sum; dette bør nok elever kjenne til. I eksempelet 2 + 3 → 5 er altså 2 og 5 er .

Algoritmer#

For addisjonsoperatoren finnes det mange algoritmer. De har forskjellige fordeler og ulemper.

Addisjon ved å telle#

Vi har allerede beskrevet en simpel addisjonsalgoritme: Man teller opp antall elementer i første addend, teller opp antall elementer i andre addend, legger dem ved siden av hverandre og teller opp antall elementer i summen.

Dette kan vi tegne opp slik:

Legg merke til at denne algoritmen (som så mange andre) er helt avhengig av en god representasjon. Vi kan bruke småsteinspråket, som i figuren, eller tall-linje; men vi kan ikke bruke vanlig siffer-representasjon.

Når vi derimot har lært oss regelen, kan vi gå direkte fra \(2 + 3\) til \(5\) uten å gå veien om å legge sammen fingre eller firkanter:

Å telle fra første addend#

La oss se på eksempelet (altså 6+3), hvor første addend er litt større. Med den simple addisjonsalgoritmen må man telle opp 6 elementer og senere telle 9. En variant med mindre jobb er da å starte fra 6 og å telle tre til: 7,8,9. Vi kan tegne opp dette ledd for ledd:

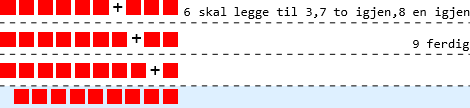
Er det egentlig sånn det foregår for små barn? TODO Småskolefolk kan sikkert si mer om dette.

blir
blir
6 + 2 blir .
5 + 1 blir .
103 + 4 blir . Riktignok har vi egentlig ikke introdusert så store tall ennå.
11 + 3 blir
100127 + 2 blir

Å telle fra første addend, men utnytte den kommutative lov#

1 + 8 blir . Hva skjedde i hodet ditt nå? Om du var innom termen 8 + 1, brukte du det vi nedenfor skal kalle den kommutative lov.

2 + 103 kan skrive om til + 2 som blir
3 + 11 blir
2 + 19 blir

Kolonnealgoritme med tiere#

Tidligere algoritme fungerer!#

Den simple algoritmen vi så på først fungerer også fint med ere. La oss se på det regnestykket (altså 21 + 13): Vi må kan “legge sammen” på en naturlig måte. Vi må sortere erne og erne for å få et tall vi kan lese på vanlig måte:

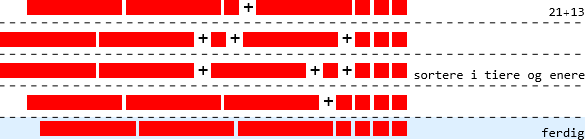
Vi kan legge merke til at det er flere inni-algoritmer her: Når vi regner ut må vi regne ut både og .

15 + 21 blir .

Sortere i kolonner#

Det er ofte praktisk å sette opp addendene under hverandre, og sortere erne og erne i egne kolonner. Da kan vi addere erne for seg og erne for seg. Dette blir mindre jobb, særlig med litt større regnestykker.

I dette dokumentet bruker vi bakgrunnsfargen bak svaret. Vi bruker stiplet linje mellom overgangene; legg merke til at det ikke er stiplet linje mellom de to øverste linjene (addendene).

Sammenlikn gjerne denne figuren med figuren over. Den likner, men er litt enklere.

Dette kan vi gjerne gjøre også i siffer-språket:

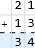
Dette kan også leses som regelen \(\overset{21 + 13}{\underset{34}{↓}}\).

blir .
blir .
blir .
23 + 34 blir (legg gjerne merke til hvordan du tenker og hvilke inni-regnestykker du bruker. Regnet du ut 2 + 3?)
52 + 24 blir .
65 + 31 blir .

Veksling / Minnesiffer#

Hva om antall ere i svaret blir mer enn 10? Da blir det fullt i høyre kolonne:
det vil si . Men tallet “tjue-elleve” (altså ) finnes ikke, eller skrives iallfall ikke sånn.

Fra må vi veksle ti ere til en er så vi får . Dette kan vi skrive (mens vi tegner vekslingen i blått)
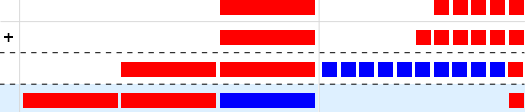, det vil si .

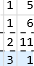Det er muligens uvanlig å sette opp en egen linje med svaret (20+11) før veksling; men vi tror dette er rimelig på et stadium både i elevenes tankeprosess og i elevenes læringsprosess.

37 + 26 blir femti-tretten som blir .
18 + 24 blir 30 + som blir .
36 + 28 blir .
18 + 7 blir .
63 + 28 blir .
36 + 22 blir .
39 + 2 blir (hvilken algoritme brukte du her?)
49 + 1 blir .
3 + 78 blir (det finnes raske måter å tenke på her).
44 + 47 blir (det er ofte vanskeligere å tenke når det er flere tilfeller av samme siffer).
22 + 22 blir .
25 + 25 blir .
En elev har regnet ut 17+4 → 11. Hva har skjedd? Hvilke representasjon tenker eleven i?

En gruppe elever fikk oppgaven 29 + 14. Dette blir selvfølgelig , men elever skrev følgende utregninger. Hva kan de ha tenkt? Hvilke representasjoner kan de ha tenkt i?

30 + 14 − 1 → 43
20 + 10 + 9 + 4 → 20 + 10 + 13 → 43
29 + 14 → 33
29 + 11 + 3 → 43
29 + 14 → 2104
29 + 14 → 313

Oppsummering: Kolonnealgoritme#

Vi har sett at småstein-representasjonsspråket (eller: røde firkant-språket) har mulighet til addere på en naturlig måte.

Kommutativ lov#

Addisjon er kommutativ. Det betyr at vi kan bytte om på rekkefølgen: \(\overset{a + b}{\underset{b + a}{⇵}}\). Dette kalles den kommutative lov, som også kan formuleres for andre operatorer.

Assosiativ lov#

Det finnes også en assosiativ lov for addisjon \(\overset{(a + b) + c}{\underset{a + (b + c)}{⇵}}\). Også denne kan formuleres for andre operatorer.

Hvordan undervise i addisjon?#

Mye tankearbeid for et enkelt regnestykke! Kanskje det kan hjelpe oss å forstå hvorfor intelligente småbarn kan synes noe så “lett” er vanskelig. Det er vanskelig å holde styr på alt dette!

4 + 3 blir .
5 + 4 blir .
5 + 1 blir (det er mulig du nå brukte en litt justert algoritme vi skal beskrive nedenfor).

Talltyper#

Man kan addere to naturlige tall (telletall) og få et nytt naturlig tall.

Man kan addere to heltall og få et nytt heltall.

Man kan også addere mange andre talltyper, for eksempel funksjoner og vektorer.

Hva kan adderes og subtraheres? Om epler og kilogram#

Hva er det som kan adderes og subtraheres?

Mange vil svare tall. Så langt har vi sett på heltall, og senere skal vi se på desimaltall.

Men vi har også addert firkanter ⬛ og hjerter ❤️. I grunn kan vi addere det meste. Vi kan addere alt som kan telles. Vi kan filosofisk diskutere om vi adderer objektene eller antallene, men i praksis gjør vi dette ofte. Vi kan addere epler 🍎.

Adderer vi to epler 🍎🍎 og tre epler 🍏🍏🍏 kan det være fristende og tidsbesparende å si “2+3” uten å nevne eplene. Noen ganger kan dette også være formålstjenlig for å abstrahere oss vekk fra det konkrete. Men ofte er det bra, og vel så riktig, å si hva vi adderer: “To epler pluss tre epler”. Da beholder elevene forbindelsen til det konkrete. Matematikken blir en modellering av virkeligheten ellers, ikke bare løsrevet teori. Det kan understøtte både motivasjon og læring. Det hjelper dessuten til å vurdere rimeligheten av svar.

Tilsvarende er praktiske problem ofte knyttet til enheter. Vi adderer 2.0 kg og 3.0 kg. Da kan det være raskest å si og skrive bare “2.0 + 3.0”. Ofte er det både bra og riktig å si også enhetene: “2.0 kg + 3.0 kg”. Det tar litt lengre tid å si, men den tida trenger elevene på å oppfatte det læreren sier uansett; og dette er enklere for elevene å forstå.

Det er forskjell på 2 kg, 2 gram, 2 meter og to epler.

Filosofi#

Symmetri#

Er \(a + b\) å ta utgangspunkt i \(a\) og legge til \(b\), eller (mer symmetrisk) å sette sammen \(a\) og \(b\)?