Delelighet

Delelighet#

Forutsetninger og læringsmål#

Vi skal diskutere når to heltall kan deles på hverandre uten rest. Vi skal også diskutere et nytt representasjonsspråk som bygger på tall-linje-språket: Stokk-representasjonen.

Vi skal også introdusere begrepet multiplum.

Dette får vi bruk for blant annet i brøkregning.

Referanser#

(Hinna & Rinvold & Gustavsen, 2016) 2.12.1 har av en eller annen grunn plassert dette under algebra.

Introduksjon#

Wiggo har 16 roser han vil dele likt i tre buketter. Hvor mange roser får vi i hver bukett??

I dette tilfellet får vi én rose til overs. Vi sier at divisjonen ikke går opp. Vi kan velge hva vi skal gjøre, avhengig av situasjonen (og av hvilke elever vi snakker til):

Vi kan regne ut at hver bukett får 0.3333… rose. Å gi bort 0.3333… roser er lite ønskelig i en romantisk situasjon.
Vi kan dele den siste rosen i tre og få ⅓ rose. Dette er også en uakseptabel løsning romantisk sett, men kan hjelpe oss å skape rettferdighet om vi skal dele sjokolade rettferdig mellom små barn. Vi kan tilmed lære barna om brøk.
Vi kan gi opp og si at vi får en rose til overs. Denne kan kastes eller gå til personen som har utført divisjonen. Vi kaller den siste sjokoladen for rest.

Denne historien beskriver . Det går også an å beskrive 15÷3 med den andre tankemodellen.

Representasjoner#

Ord#

Om et delestykke a÷b er likt et heltall q, sier vi at

a er delelig med b eller delbart med b
a er et multippel av b
b går opp i a
b er faktor i a: Med en formel b|a

Ellers, om a÷b = q + r (r < b), sier vi at

De er ikke delelige, går opp etc
r er rest (er “til overs”)
a modulo b er lik r. Overgang til modulærregning som ofte blir omtalt i algebraiske strukturer.

Småstein#

Vi bruker representasjoner fra divisjon. Dermed får vi også en repetisjon av delings- og målingsdivisjon. Gruppene i egen farge, selv om det selvfølgelig ikke er nødvendig.

Delingsdivisjon#

delt i grupper blir .

Hver gruppe er 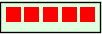det vil si .

, derimot, delt i grupper går ikke opp. Vi får med i rest.

Målingsdivisjon#

delt i grupper som er så store som 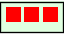blir .

Antallet grupper blir altså .

, derimot, delt i grupper så store som , går ikke opp. Vi får med i rest.

Fliser#

Et tall (f.eks. 15) kan deles på et annet (3) om det kan legges i et rektangel med det andre som sidelengde:

Snakker vi om delingsdivisjonen tegnes sidelengden vertikal til høyre; snakker vi om delingsdivisjon tegnes sidelengden horisontal nederst.

16 kan ikke legges i noe rektangel med 3 som sidelengde.

Formelspråk#

Om a er delbart med b, skriver vi b|a; legg merke til rekkefølgen! Tegnet “|” kan best leses “er faktor i”. 3|15.

Legg også merke til at dette betyr at a = bn, hvor n er et heltall. 15 = 3 × n.

Tall-linje#

Et tall er delelig med 3 hviss det er et helt antall 3ere. Tallene som er delelig med 3 ligger i et mønster bortover bortover. Her er de første:

Tegn en tall-linje fra 0 til 20. Merk av alle heltall som er delelig med 4.

Tallene som er delelig med 2 har et eget navn: De kalles partall,*tall".

Tømmerstokk-språket#

Vi vil nå introdusere tømmerstokk-språket. Det er en blanding av tall-linje, småstein og regnefortelling om tømmerstokker. Det inneholder ikke så mye nytt, men er litt enklere å tegne i praksis.

I språket er et heltall \(n\) representert ved en tømmerstokk med lengde \(n\). Tømmerstokkene blir av latskap tegnet som rektangler. 3 blir

Multippel (multiplum), felles multippel og minste felles multippel#

Legger vi 3-tømmerstokker bortover, kommer vi til alle tall som er delelig på 3:

Spør vi om 15 er delelig med 3, kan vi altså spørre: Kan vi legge 3-tømmerstokker bortover etter hverandre så de tilsammen blir like lang som en 15-stokk?

Vi skal kalle disse tallene multipler av 3. Et multippel av a er et tall som er lik a×n, hvor n ∈ ℕ. En tømmerstokks multipler er alle lengdene vi kan få med å legge sånne tømmerstokker etter hverandre. Multipler til 3 er alle tallene vi kan få med å si 3+3+3… et helt antall ganger, altså {3, 6, 9, 12, 15, 18, 21, 24, …}. Multipler til 4 er {4, 8, 12, 16, 20, 24, …}. Multipler til 6 er {6, 12, 18, 24, …}.

Ordforklaring: Multippel

Ordet multippel kommer av multiplikasjon. Ordene multippel og multiplum er språklige varianter for det samme. I flertall vil vi si multipler.

Felles multippel#

To tall kan ha noen felles multpler. Vi ser at 3 og 4 har 12 og 24 som felles multipler.

Om vi legger tre-tømmerstokker etter hverandre og fire-tømmerstokker ved siden av hverandre vil de “treffe hverandre” etter 12 og 24.

Produktet av to tall er alltid et felles multippel. Faktisk er alle multipler av produktet av to tall felles multipler av tallene.

Legg merke til at 4 3-stokker blir samme lengde som 3 4-stokker; det er ikke tilfeldig.

Dette skal vi senere bruke når vi skal addere brøker: Skal vi addere brøker, bør vi splitte dem så de får felles nevner; denne nevneren må være en felles multippel av de opprinnelige nevnerne. Skal vi addere tredeler og firedeler må vi splitte dem til 12deler eller 24deler.

Minste felles multippel#

Det følgende er etter Ellefs mening ikke så viktig som det engang var:

Det hender det finnes multipler som er mindre enn to tall. Et eksempel er 4 og 6: Produktet er 24, men det finnes også et multippel ved 12. Tidligere la man stor vekt på å finne minste felles multiplum. I vår digitale tidsalder har vi lite å tjene på dette, og Ellef anbefaler de aller fleste å bruke den enklere veien det er å bare multiplisere de to tallene. Da finner man alltid et multiplum, om enn ikke alltid det minste.

Algoritme: Om man ønsker å finne minste felles multiplum av to tall må man faktorisere tallene, og ta bag-wise snitt av faktorene. For mer informasjon, se for eksempel matematikk.net om fellesnevner.

Legg merke til at 4 og 6 har felles faktor 2; 24 delt på 12 er samme tallet. Det er ikke tilfeldig.

Senere skal vi kontrastere Minste Felles Multiplum med Største Felles Faktor.

Et morsomt bevis#

Bevis (fra MA302): a er delelig med c, b er delelig med c, (a+b) er delelig med c. Tømmerstokk-representasjon. Først eksempel i representasjon, så ser man at “sånn må det jo alltid være.

Regneark#

Excel har funksjonene QUOTIENT (norsk: KVOTIENT) for heltallsdivisjon og MOD (norsk: REST) for å finne rest.

Python#

Python har operatoren % for å finne rest: 16 % 5 gir 1. Deler man heltall med // får man heltallsdivisjon, altså 16 // 5 gir 3.

Algoritmer#

Legge i rektangel #

Kan tallet a deles på b? Man kunne jo prøve seg fram; men litt mer effektivt er det å legge a småstein i rektangel med sidelengder b.

Sjekke delelig med bestemte tall#

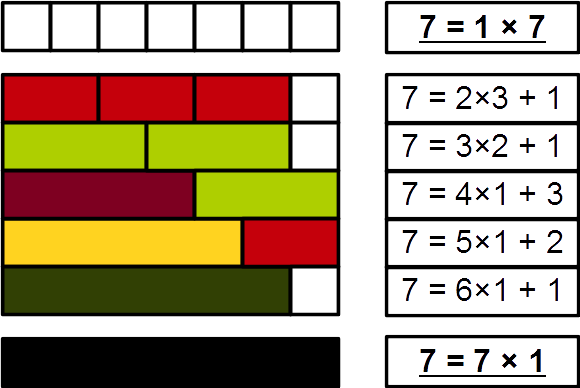
../../_images/Prime_number_Cuisenaire_rods_7.png — Fig. 1.4 7 er primtall.
Venstre kolonne likner tømmerstokker.
Wikimedia / Hyacinth#

Vi skal nå gå gjennom en del huskeregler for å sjekke om et tall a er delelig på forskjellige andre tall.

Ordforklaring: Hviss

“Hviss” med to s-er betyr her “hvis og bare hvis”. Et fremmedord er ekvivalens. Et symbol er ⇔.

De følgende reglene gjelder bare i titall-systemet. De er ganske sære, og det er vanskelig å få en relasjonell forståelse til dette, fordi reglene er så “tilfeldige” i den forstand at det er “tilfeldig” at vi har et titall-system.

Delelig på 1? Ikke interessant#

Siden alle tall er delelig på 1 (og seg selv), er dette ikke særlig interessant.

TODO Stokkdiagram nedover her

Delelig på 2? Siste siffer#

Først en regel for å sjekke om et tall er partall:

Et tall er delelig på 2 hviss siste siffer i tallet er delelig på 2. Om siste siffer er 0, 2, 4, 6 eller 8 vet vi altså at tallet er delelig på 2. Er siste siffer et oddetall vet vi at det ikke er delelig på 2.

Delelig på 3? Tverrsum#

Først må vi definere tverrsummen til et heltall. Vi skal introdusere det på tre måter:

Tverrsummen er summen av tallets sifre. Tverrsummen av 134 er altså 8; tverrsummen av 489 er altså 21. I følge denne definisjonen kan altså en tverrsum ha flere sifre.
Tverrsummen er summen av tallets sifre, eller tverrsummen av en tverrsum. I følge denne definisjonen kan altså tverrsummen av 489 være 21 eller 3.
Den minste tverrsummen er den minste mulige tverrsum; her er det altså ikke mulig å summere sifre, og antall sifre må være 1.
Det er også mulig å definere den minste tverrsummen som en algoritme: Du adderer sifre i tallet inntil det ikke går lengre.

Vi tar også med at vi alltid kan trekke 9 fra en tverrsum, så forblir tverrsummen den samme.

Så til regelen: Et tall er delelig på 3 hviss tverrsummen er delelig på 3. Om tverrsummen er 3, 6 eller 9 vet vi altså at tallet er delelig på 3.

Delelig på 4?#

Dette trenger vi sjelden å sjekke: Det er vanligvis enklere å først sjekke om tallet er delelig på 2 og så om det er delelig på 2 igjen.

Vi kan nevne en regel likevel: Et tall er delelig på 4 hviss de to siste sifrene er delelig på 4.

Delelig på 5? Siste siffer#

Et tall er delelig på 5 hviss siste siffer i tallet er delelig på 5. Om siste siffer er 0 eller 5 vet vi altså at tallet er delelig på 5.

Delelig på 6, 8, 12?#

Dette er ikke-primtall. Her kan vi først sjekke om tallet er delelig på 2 og så om det er delelig på 3.

Delelig på 7, 11, 13?#

Her finnes det bare ganske sære regler.

Delelig på 9#

Et tall er delelig på 9 hviss tverrsummen er delelig på 9.

Delelig på 10#

Et tall er delelig på 10 hviss siste siffer er 0. Altså må siste siffer være delelig på 0.

Oppgave#

Lag en liste over de 30 første naturlige tall og deres faktorer. Du kan f.eks. bruke et regneark og la hvert tall få en rad (linje).

Når divisjonen ikke går opp: Alternativ#