Null#

Introduksjon#

Tom har fire sjokolader, men spiser fire. Hvor mange har han igjen? Hva er 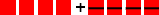(altså 4−4)?

Snakker vi om sjokolader, blir svaret “ingen sjokolader”. På en tall-linje blir det tallet “på midten”, det som er helt til venstre på tall-linja vi begynte med og som nå er mellom −1 og 1. Dette tallet, “ingen”, trenger spesielle representasjoner.

Representasjoner av 0#

Vi definerer noen representasjoner. Noen av representasjonene er nye, mens andre følger naturlig av tidligere representasjonesspråk.

  • Formelspråket: “”. Dette kom relativt sent i matematikkhistorien, lenge etter de andre sifrene. Kanskje symbolet, og begrepet, kom sent fordi 0 er vanskelig å se for seg og representere?

  • Ord: “Null”. Vi bruker også ord som “ingen” eller “ingenting”.

  • Tall-linjespråket: 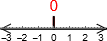. Dette er naturlig.

  • Småstein: Her har vi ikke noe naturlig symbol ennå. Vi definerer (som kanskje likner på en “tom” firkant? som kanskje likner på sifferet 0?)

Regning med 0#

Addisjon#

Har vi fem sjokolader og legger til ingen, har vi fortsatt fem sjokolader. + blir . \(\overset{a + 0}{\underset{a}{⇵}}\).

Har vi ingen sjokolader og legger til fem, får vi fem sjokolader. \(\overset{0 + a}{\underset{a}{⇵}}\). Dette kan henger også sammen med forrige lov ved hjelp av kommutativitet.

  • 17 + 0 blir .

  • 0 + 164 blir

Subtraksjon#

Har vi fem sjokolader og fjerner ingen, har vi fortsatt fem sjokolader. − blir . \(\overset{a - 0}{\underset{a}{⇵}}\).

Har vi ingen sjokolader og fjerner fem, får vi grinete unger. Dette kan vi representere på en tall-linje: Vi starter i 0 og går 5 mot venstre. Vi kommer da til −5. \(\overset{0 - a}{\underset{-a}{⇵}}\). I eksemplet hadde \(a\) verdien 5; om vi lager et annet eksempel hvor \(a\) har verdien −5, får vi ved regelen at 0 − −5 blir −−5; dette blir så til +5.

Tall alene −0#

Hva er −0? Dette er altså tallet like langt fra 0 som +0. Vi får at +0 = −0. 0 er det eneste tallet hvor minus tallet blir tallet selv.