1.1.12. Potens#
Forutsetninger og læringsmål#
Vi skal nå introdusere potenser. Vi forutsetter spesielt multiplikasjon.
Referanser#
- 6. klasse: formulere og løse problemer fra sin egen hverdag som har med desimaltall, brøk og prosent å gjøre, og forklare egne tenkemåter
- 8. klasse: bruke potenser og kvadratrøtter i utforsking og problemløsing og argumentere for framgangsmåter og resultater
- 10. klasse: utforske sammenhengen mellom konstant prosentvis endring, vekstfaktor og eksponentialfunksjoner
(Hinna & Rinvold & Gustavsen, 2016) 2.10 s.272 Av en eller annen grunn har QED plassert potensregning under algebra.
Oppgaver fra Ndla om eksponentiell vekst og om smittespredning og R-tall
Introduksjon: Virus#
Dag 0 finnes bare ett virus. Antallet virus tredobles hver dag. Hvor mange har vi etter fire dager?
En biolog ville nok helst snakke om en viruspartikkel eller ett virion, men vi skal for enkelhets skyld snakke om ett virus. Flertall er norsk “virus” og engelsk “viruser”, selv om latin har “vira”.
Repetert multiplikasjon#
Vi husker kanskje at multiplikasjon n×a kan sees som repetert addisjon: a+a+a… n ganger.
År 0 har vi 1 virus.
År 1 har vi 3 virus.
År 2 har vi 3×3, altså 9, virus.
År 3 har vi 3×3×3, altså 27, virus.
År n har vi 3×3… n ganger virus.
CO2#
Gå til https://ourworldindata.org/co2-emissions . Kan jordas CO2-utslipp modelleres rimelig bra som en eksponentiell kurve?
Representasjoner#
Ord#
En potens er et tall grunntall som blir multiplisert med seg selv eksponent ganger.
Grunntallet kalles også base, og jeg kan ikke love å være konsekvent i dette dokumentet. Det kan også kalles vekstfaktor.
Fig. 1.11 Gir potens?#
Eksponenten kan være antall runder, antall dager e.l.
Vi sier at base er opphøyd i eksponenten, for eksempel at tre er opphøyd i fem, eller at tre er opphøyd i femte potens.
Ordforklaring: Potens
Ordet potens betyr noe sånt som “sterk, mulighet” og reiser seg fort til store tall. Under noe tvil tar i med bildet til høyre for å huske.
Populærkulturen bruker uttrykket gå viralt for noe som likner på eksponensiell vekst.
Formelspråket#
I formelspråket skriver vi vanligvis \(a^n\) for base a og eksponent n; for eksempel \(3^5\). Oftest er \(n\) et positivt heltall; derav \(n\). Vi unngår å bruke \(e\), som betyr noe helt annet.
I typografiske sammenhenger hvor dette er vanskelig bruker vi tegnet ^ (caret). \(a^n\) betyr altså det samme som \(a\)^\(n\). ^ er altså en operator på nøyaktig samme måte som + og ×, selv om vi av historiske grunner skriver den på den spesielle måten \(a^b\).
3^2 er .
Senere skal vi se at Unicode har egne tegn for en del eksponenter, f.eks. ² og ⁿ. De er noen ganger enklere å skrive inn enn å bruke spesialformelverktøy, iallfall om man har program som WinCompose. Mange liker også å skrive inn potenser med LaTeX eller med håndskriftsgjenkjenning.
Assosiativitet#
Om vi ser \(2^{3^4}\), skal vi tolke det som \(\left(2^3\right)^4\) eller som \(2^\left(3^4\right)\)? De gir jo forskjellige svar.
De viser seg at vår kultur ikke har blitt enig om dette. Om vi skriver inn 2^3^4 vil Microsoft Excel, Google og Wolfram Alpha gi forskjellig svar. LaTeX godtar ikke at vi skriver 2^3^4; vi må ha parenteser for å klargjøre om vi mener {2^3}^4 (som blir \({2^3}^4\)) eller 2^{3^4} (som blir \(2^{3^4}\), med litt andre størrelser på eksponentene).
Skriv uttrykket 2^3^4 inn i et regneark, i Google og i wolframalpha.com. Sammenlikn svarene. Hva skjer? Husk at en operators venstre- og høyreassosiativitet ikke er en matematisk egenskap ved operatoren, men vår kulturs måte å tolke på.
Det er at potensoperatoren er assosiativ. Husk å sjekke både venstre- og høyreassosiativitet!
Det er at potensoperatoren er kommutativ. Uttrykket \(a^b\) kan også representeres med et operatorsymbol, for eksempel ^, altså \(a\)^\(b\).
Gjentatt multiplikasjon#
Vi husker kanskje at multiplikasjon kan illustreres med gjentatt addisjon.
3×2 kan for eksempel illustreres
.2×2:
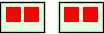
2×2×2:
2×2×2×2:
2×2×2×2×2:
.
Dette blir fort uleselig ved store grunntall eller eksponenter, men kan hjelpe oss å få et begrep om hva potenser er snakk om.
I dette tilfellet gikk eksponenten “nedover”; om vi skulle tegnet på en mørkerød pil måtte den gå nedover.
Trestruktur#
Sammenlikn denne figuren med denne:
Dette er altså en representasjon av 2⁴. Grunntallet 2 betegner hvor mange grener som kommer fra hvert punkt, og eksponenten betegner antall etasjer.
Vi kan også tegne treet mot høyre:
Fingre#
Dette er en representasjon av fem,tallord opphøyd i andre,ordens-tallord:
Fliser#
Vi gjentar at \(a^n\) betyr \(a·a·a·…\) multiplisert \(n\) ganger. \(n\) er på en måte lengden på rekka med \(a\)-er. Det hender derfor at vi legger en strek over \(a\)-ene for å representere \(n\):
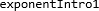Vi bruker i disse dokumentene fargen
for eksponenter, blant annet for denne streken. Vi kan også merke eksponenten over streken:
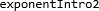, for eksempel 
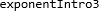. En ulempe er riktignok at denne streken er mulig å forveksle med en brøkstrek.
Vi kan også sette inn i representasjonen operatoren ^ og basen (som kommer til venstre, både fordi den kommer “før” svaret og fordi basen og eksponenten nå er plassert på en måte som passer med skrivemåten \(a^n\) for eksempel \(3^4\)):
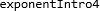. Endelig kan vi sette på våre vanlige farger:
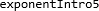. Da kan vi også gjøre ting som 
.
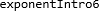Dette er ikke like elegant som representasjonene for multiplikasjon og divisjon. Vi har ikke områder under som hjelper oss å finne svaret. Men representasjonen kan uttrykke en del sannheter om potenser, og hjelpe oss å huske ting.
Å tegne opp hele densiste representasjonen er for arbeidskrevende å gjøre til daglig. Men det hender ofte jeg bruker forenklede varianter, for eksempel en strek over en rekke av grunntall, når jeg arbeider til vanlig.
I virus-eksempelet kan streken, og retningen mot høyre, tolkes som en tidslinje.
Senere skal vi komme bort i situasjoner hvor vi vet grunntallet og potensen, men skal finne eksponenten. Dette er logaritmeregning. Vi skal altså “finne lengden på den røde streken”. Dette kan greit representeres med representasjonen vi lager nå, selv om algoritmene er ganske kompliserte.
Søylediagram#
Det følgende er eksperimentelt.
Dermed blir det også mulig å representere potens som søylediagram, hvor høyden på hver søyle er grunntallet og antall søyler er eksponenten. Eksponenten går altså som vanlig mot høyre, mens eksponenten er tegnet oppover. Søylene skal så å si multipliseres med hverandre.
Dette er ikke noen selvfølgelig representasjon om man ikke er vant til den. Videre erfaring må vise om den er god.
Representasjonsspråket henger sammen med noen vi har lært før. Søylediagram-representasjonen for f.eks. 3⁵ kan minne om 3·3·3·3·3. Representasjonsspråket henger også sammen med flisspråket. Fliser dannes med å stable addisjon (gjentatt addisjon); søyler dannes ved å stable multiplikasjon (gjentatt multiplikasjon). Søylediagram-språket peker også i retning av grafen under.
Det viser seg også at representasjonen illustrerer en del lover ganske godt.
Graf i koordinatsystem #
Vi har egentlig ikke introdusert koordinatsystem eller grafer ennå, men tar likevel med oss potensfunksjonen som en graf. Eksponenten går her mot høyre (på x-aksen), mens potensverdien kommer oppover (på y-aksen). For hver enhet eksponenten øker (mot høyre) blir potensen doblet (oppover). Den blir “doblet” siden vi her har base .
Eksponenten går som vanlig mot høyre; i søylediagrammene tegnet vi grunntallet oppover, men nå tegner vi verdien oppover.
Oppgaver:
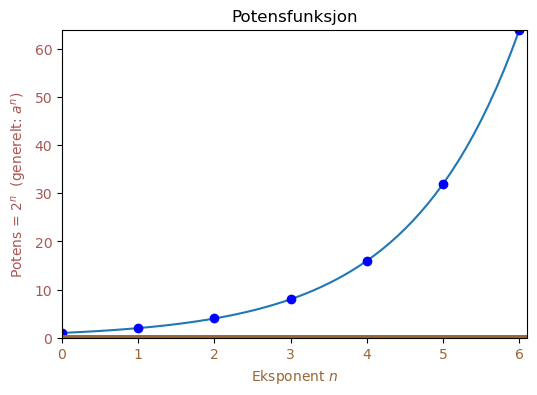
Hvor er \(2^3\) i kurven over?
Hvor er \(2^1\) i kurven over?
Oppgave: Lag en liknende kurve i GeoGebra. La grunntallet være bestemt av en glider.
Algoritmer#
Regne ut ved multiplikasjon#
Når vi skal regne ut potenser reduserer vi dem typisk til multiplikasjon.
Spesielt interessante grunntall#
Som vanlig advarer vi mot ensidig fokus på å pugge formler instrumentelt; det er viktigere å ha gode representasjoner og forstå begreper relasjonelt.
Grunntallet er altså hva som blir multiplisert med seg selv: I \(a^n\) er grunntallet a.
10ⁿ#
Det enkleste er kanskje å utforske selv:
10² er
10³ er
10⁴ er Legg merke til at når vi øker eksponenten med 1, multipliserer vi potensen med 10.
10⁵ er Legg merke til at om vi går bakover og minker eksponenten med en, dividerer vi potensen med 10.
I de følgende oppgavene reduserer vi eksponenten med 1 og 1.
10² er (som sagt)
10¹ er . Dette følger av definisjonen.
10⁰ er . Dette følger ikke direkte av det vi har sagt, men det er vel lov til å gjette. Senere kan vi bevise.
10⁻¹ er =$1,$2. Vi har egentlig ikke introdusert negative eksponenter. Legg merke til at \(10^{-1} = \frac{1}{10^1}\).
10⁻² er =$1,$2. Vi har egentlig ikke introdusert negative eksponenter. Legg merke til at \(10^{-2} = \frac{1}{10^2}\).
Noen snakker om at eksponenten “angir antall nuller i svaret”.
Titallsystemet bygger igrunn på 10ⁿ. Siffer nummer n mot venstre, regnet fra desimalskilletegnet, har verdi lik sifferet×10ⁿ⁻¹. Om det for eksempel i tallet 1234 står 3 på plass nummer 2, har det verdi 3×10²⁻¹ (dvs. 30).
Dette kan tydeliggjøres ved å skrive tallet på utvidet form. 1234 skrevet på utvidet form er 1×10³ + 2×10² + 3×10¹ + 4×10⁰. Utvidet form er viktig i småskolen, men kanskje ikke over 5. klasse?
En annen form er standardform (se også (Hinna et al, 2016) 2.10.2 s.286). Et tall skrevet på standardform er skrevet på formen a×10ⁿ, hvor a vanligvis er mellom 1 og 10 (har ett siffer; noen ganger opp til tre eller flere) og n er et heltall. 4321 skrevet på standardform er 4.321×10³.
2ⁿ#
Man kan gjerne kunne noen av disse potensene utenat. Det er spesielt praktisk om man er IT-nerd eller om man har en datter på seks år som stadig spør “hva er det dobbelte av…”?.
2¹ er
2² er
2³ er
2⁴ er Legg merke til at når vi øker eksponenten med 1, multipliserer vi potensen med grunntallet.
2⁵ er Legg merke til at om vi går bakover og minker eksponenten med en, dividerer vi potensen med grunntallet.
2¹⁰ er 1024, som tilfeldigvis er nesten lik 10³.
I de følgende oppgavene reduserer vi eksponenten med 1 og 1.
2⁰ er .
2⁻¹ er$1,$2. Vi har egentlig ikke introdusert negative eksponenter. Legg merke til at \(2^{-1} = \frac{1}{2^1}\).
2⁻² er$1,$2. Vi har egentlig ikke introdusert negative eksponenter. Legg merke til at \(2^{-2} = \frac{1}{2^2}\).
Moore’s lov sier (unøyaktig gjengitt) at en datamaskin blir dobbelt så rask annethvert år. Mer nøyaktig: Antall transistorer i en datamaskin dobler seg annethvert år. Det vokser altså eksponentielt (med et grunntall √2).
1ⁿ#
1¹ er
1² er 1·1 som er
1³ er 1·1·1 som er
1⁴³² er
En opphøyd i minus Norges befolkning er
Hvordan blir kurven til funksjonen \(1^x\)?
0ⁿ#
0¹ er
0² er 0·0 som er
0³ er 0·0·0 som er
0⁴³² er
0ⁿ = 0 for positive n.
Hvordan blir kurven til funksjonen \(0^x\)?
\((ab)^n\) (produkt som grunntall)#
I formelspråket#
(ab)ⁿ må være lik
ab·ab·ab… multiplisert n ganger. Dette kan ordnes til
a·a·a…·b·b·b… hvor a og b forekommer n ganger hver. Dette er altså
aⁿ·bⁿ.
Vi har regelen \(\overset{(ab)^n}{\underset{a^n·b^n}{↓}}\).
Om dette er litt vanskelig å holde styr på kan det være nyttig å lage et eksempel. Om for eksempel n er 3, har vi at (ab)³ = ababab = aaabbb = a³·b³.
Regelen som eksempel på bevis#
Vi tar med noen prinsipp om bevisbasert undervisning som kan være brukbare her:
Nårm an introduserer dette kan man godt ta utgagnspunkt i et eksempel (for eksempel (ab³)). Dette tjener for å bygge intuisjon; det kan også være grunnlaget for et generisk eksempel.
Om elevene får oppdage og utlede regelen \(\overset{\left(ab\right)^n}{\underset{a^n·b^n}{⇵}}\) selv er det større sjanse for at de forstår og husker den enn om en lærer skulle presentere regelen ferdig.
Når vi har argumentert for regelen kan vi så bruke denne regelen seinere.
\((b^n)^m\) (potens som grunntall)#
\((b^n)^m\) må være bⁿ·bⁿ·bⁿ·bⁿ… multiplisert m ganger. bⁿ er b·b·b… multiplisert n ganger.
Om dette er litt vanskelig å holde styr på kan det være nyttig å lage et eksempel. Hvor mye er
(b³)⁴ (hvor altså n er 3 og m er 4)? Dette må altså være
(b³)×(b³)×(b³)×(b³) (altså fire ganger). Dette blir igjen
(b·b·b)×(b·b·b)×(b·b·b)×(b·b·b) (altså fire parenteser med tre ber i hver). Vi bruker to typer multiplikasjonstegn bare for å skaffe litt oversikt. Siden vi har fire grupper med tre ber i hver, ser vi at antall ber tilsammen må være tre ganger fire. Det ser altså ut til at vi ender med
b⁽³⁴⁾ altså b¹².
Vi har regelen \(\overset{(b^n)^m}{\underset{b^{n·m}}{↓}}\).
\((a+b)^n\) (produkt som grunntall)#
Går utenfor det vi skal kunne i MA101. Om \(n ↦ 2\) har vi 1. kvadratsetning. Se videre i Wikipedia om Pascals trekant
Spesielt interessante eksponenter#
Eksponenten er altså hvor mange ganger grunntallet blir multiplisert med seg selv. I \(a^n\) er grunntallet n. I et koordinatsystem er grunntallet . I en rekke \(a^n = a·a·a·a·…·a\) er eksponenten
Fig. 1.12 \(4^3\)#
a³ (kube)#
a³ er utifra definisjonen lik a×a×a. Dette kalles kube, kubikk-tall e.l. og er assosisert med volum.
a² (kvadrat)#
a² er utifra definisjonen lik a×a. Dette kaller vi kvadrat av a; det er assosiert med areal.
Elever bør kvadrattall. De er en del av den lille gangetabellen, og bør kjennes forlengs og baklengs. Derfor må lærere også øve på dem. Vi tar oss tid her:
0² er 0·0 som er
1² er 1·1 som er
2² er
3² er
4² er
5² er
6² er
7² er
8² er
9² er
10² er
11² er Noen vil gå over til å bruke flismodell her.
12² er
100² er
Disse bør altså kunnes forlengs og baklengs:
36 er ²
25 er ²
a¹#
a¹ er utifra definisjonen lik a for alle a.
314¹ er
Hvor ligger punktet \(a^1\) på koordinatsystem-representasjonen av en potens? Se for deg punktet for et par-tre grunntall.
a⁰#
a⁰ er ikke rett fram utifra definisjonen på potens. Hvordan skal vi definere dette?
Det enkleste er kanskje å sette opp en tabell a la det vi gjorde for 10 og 2:
a³ = a·a·a
a² = a·a
a¹ = a Og så observere at når man går en linje “nedover” reduserer vi eksponenten med 1 samtidig som vi dividerer med a. Da kan vi fortsette mønsteret:
a⁰ =
0⁰ er mer komplisert.
Hvor ligger punktet \(a^0\) på koordinatsystem-representasjonen av en potens? Se for deg punktet for et par-tre grunntall.
a⁻¹ og negative eksponenter#
Vi nevnte denne regelen såvidt under brøk.
Vi kan fortsette mønsteret:
a⁻¹ = 1/a¹
a⁻² = 1/a²
⋮
a⁻ⁿ = 1/aⁿ
(Hinna et al, 2016) 2.10.1 s.283
Lag kurven f(x) = a^x i GeoGebra, hvor a er en glider som kan ha negative og positive verdier.
\(a^½\) og andre brøker i eksponenter#
Det viser seg at \(b^\frac{1}{2} = \sqrt{b}\). Det er altså forbindelse mellom eksponent og kvadratrot.
Mer generelt: \(b^\frac{t}{n} = \sqrt[n]{a^t}\)
Hvor ligger punktet \(a^\frac{1}{2}\) på koordinatsystem-representasjonen av en potens?
Vi tar med et utsnitt av grafen for 2ⁿ:
Sum som eksponent; produkt av potenser med samme grunntall#
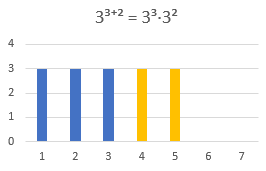
\(b^{n + m}\) må være \(b·b·b…\) multiplisert \(n+m\) ganger. Dette må være lik \(b^n·b^m\). Vi har altså regelen \(\overset{b^{n + m}}{\underset{b^n·b^m}{↓}}\).
Regelen kan også brukes den andre veien — til å multiplisere eksponenter med samme grunntall.
Differanse som eksponent; divisjon/forkorting av potens med samme gurnntall#
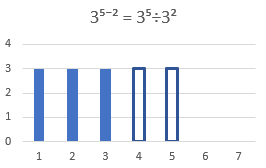
TODO
Hvor ligger punktet \(a^\frac{1}{2}\) på koordinatsystem-representasjonen av en potens?
Faktorisere potenser#
Potensen \(a^n\) kan altså skrives som \(a·a·a…·a\) med \(n\) \(a\)-er.
\(a^3 ↔ a·a·a\).
\(a^2 ↔ a·a\).
\(a ↔ a\).
\(a^0 ↔ 1\).
\(a^{-1} ↔ \frac{1}{a^1} ↔ \frac{1}{a}\).
\(a^{-2} ↔ \frac{1}{a^2} ↔ \frac{1}{a·a}\).
\(a^{-3} ↔ \frac{1}{a^3} ↔ \frac{1}{a·a·a}\).