2.3.10. Utvalg av en populasjon

TODO modellering referanse

Forutsetninger og læringsmål

Vi skal se på et aspekt med statistikk som er mye brukt i vitenskap, selv om det nok ligger utenfor det vi skal lære i MA102 (?).

Referanser

(Klaveness et al, 2019) 26s210 Sannsynlighet og spill intro

Introduksjon

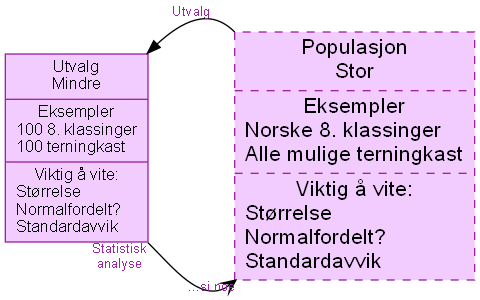
Den generelle situasjonen er: Vi ønsker å si noe om en stor populasjon (f.eks. alle norske 8. klassinger). Det er bare praktisk å måle et utvalg (f.eks. 100 stykker). Hva kan vi si om populasjonen basert på våre målinger — og hvor sikkert kan vi si det?

En populasjon er norske 8. klassinger. To parametre fra denne populasjonen er alder og karakter. Man kan ta et utvalg fra populasjonen — for eksempel elevene fra tre konkrete 8. klasser.

Referanser

God innføring av Pripp (2017) i Tidsskrift for Den Norske Legeforening

Eksempler

Høyde

Vi er interessert i høyden på norske 8. klassinger.

Undervisningsmetoder

Vi er interessert i om undervisningsmetodene “oppmuntring” eller “dask på lanken” gir best resultat.

Representasjoner

TODO Move some of these to representations of parameters

Frekvensdiagram

#### Unused: B
import matplotlib.pyplot as plt
import numpy as np
import numpy.random as ran

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 100 # Number of samples
average = 180 # Average
dev = 20 # Standard deviation
steps = 10 # group width for display
#sample = numpy.random.Generator.binomial(180, 1, size)
sample = np.random.normal(average, dev, size)
#print(sample)
#bin = np.arange(0,average,10)

n, bins, patches = plt.hist(sample, bins=24, range=(120, 240), edgecolor="#9C23A6", color="#F2CCFF", linestyle="dashed") 
plt.title("Binomial Distribution") 
# add a 'best fit' line  https://matplotlib.org/stable/gallery/statistics/histogram_features.html
y = ((1 / (np.sqrt(2 * np.pi) * dev)) *
     np.exp(-0.5 * (1 / dev * (bins - average))**2))*average*4
#print(bins)
#print(y)

plt.plot(bins, y,color="#F2CCFF", linestyle="dashed")
plt.ylabel("frekvens")
#plt.xlabel("Utfallsrom: høyde")
#plt.xticks(bins-5, bins)
plt.axvline(average, color="#9C23A6", linestyle='dashed', linewidth=3)
min_ylim, max_ylim = plt.ylim()
plt.text(average+10, max_ylim*0.9, 'Mean: {:.2f}'.format(average), color="#9C23A6")
plt.plot([average-dev,average+dev], [1,1])

plt.savefig("images/aaaab.png")
#plt.show()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
Cell In[1], line 36
     33 plt.text(average+10, max_ylim*0.9, 'Mean: {:.2f}'.format(average), color="#9C23A6")
     34 plt.plot([average-dev,average+dev], [1,1])
---> 36 plt.savefig("images/aaaab.png")

File ~\anaconda3\lib\site-packages\matplotlib\pyplot.py:1023, in savefig(*args, **kwargs)
   1020 @_copy_docstring_and_deprecators(Figure.savefig)
   1021 def savefig(*args, **kwargs):
   1022     fig = gcf()
-> 1023     res = fig.savefig(*args, **kwargs)
   1024     fig.canvas.draw_idle()  # Need this if 'transparent=True', to reset colors.
   1025     return res

File ~\anaconda3\lib\site-packages\matplotlib\figure.py:3343, in Figure.savefig(self, fname, transparent, **kwargs)
   3339     for ax in self.axes:
   3340         stack.enter_context(
   3341             ax.patch._cm_set(facecolor='none', edgecolor='none'))
-> 3343 self.canvas.print_figure(fname, **kwargs)

File ~\anaconda3\lib\site-packages\matplotlib\backend_bases.py:2366, in FigureCanvasBase.print_figure(self, filename, dpi, facecolor, edgecolor, orientation, format, bbox_inches, pad_inches, bbox_extra_artists, backend, **kwargs)
   2362 try:
   2363     # _get_renderer may change the figure dpi (as vector formats
   2364     # force the figure dpi to 72), so we need to set it again here.
   2365     with cbook._setattr_cm(self.figure, dpi=dpi):
-> 2366         result = print_method(
   2367             filename,
   2368             facecolor=facecolor,
   2369             edgecolor=edgecolor,
   2370             orientation=orientation,
   2371             bbox_inches_restore=_bbox_inches_restore,
   2372             **kwargs)
   2373 finally:
   2374     if bbox_inches and restore_bbox:

File ~\anaconda3\lib\site-packages\matplotlib\backend_bases.py:2232, in FigureCanvasBase._switch_canvas_and_return_print_method.<locals>.<lambda>(*args, **kwargs)
   2228     optional_kws = {  # Passed by print_figure for other renderers.
   2229         "dpi", "facecolor", "edgecolor", "orientation",
   2230         "bbox_inches_restore"}
   2231     skip = optional_kws - {*inspect.signature(meth).parameters}
-> 2232     print_method = functools.wraps(meth)(lambda *args, **kwargs: meth(
   2233         *args, **{k: v for k, v in kwargs.items() if k not in skip}))
   2234 else:  # Let third-parties do as they see fit.
   2235     print_method = meth

File ~\anaconda3\lib\site-packages\matplotlib\backends\backend_agg.py:509, in FigureCanvasAgg.print_png(self, filename_or_obj, metadata, pil_kwargs)
    462 def print_png(self, filename_or_obj, *, metadata=None, pil_kwargs=None):
    463     """
    464     Write the figure to a PNG file.
    465 
   (...)
    507         *metadata*, including the default 'Software' key.
    508     """
--> 509     self._print_pil(filename_or_obj, "png", pil_kwargs, metadata)

File ~\anaconda3\lib\site-packages\matplotlib\backends\backend_agg.py:458, in FigureCanvasAgg._print_pil(self, filename_or_obj, fmt, pil_kwargs, metadata)
    453 """
    454 Draw the canvas, then save it using `.image.imsave` (to which
    455 *pil_kwargs* and *metadata* are forwarded).
    456 """
    457 FigureCanvasAgg.draw(self)
--> 458 mpl.image.imsave(
    459     filename_or_obj, self.buffer_rgba(), format=fmt, origin="upper",
    460     dpi=self.figure.dpi, metadata=metadata, pil_kwargs=pil_kwargs)

File ~\anaconda3\lib\site-packages\matplotlib\image.py:1689, in imsave(fname, arr, vmin, vmax, cmap, format, origin, dpi, metadata, pil_kwargs)
   1687 pil_kwargs.setdefault("format", format)
   1688 pil_kwargs.setdefault("dpi", (dpi, dpi))
-> 1689 image.save(fname, **pil_kwargs)

File ~\anaconda3\lib\site-packages\PIL\Image.py:2428, in Image.save(self, fp, format, **params)
   2426         fp = builtins.open(filename, "r+b")
   2427     else:
-> 2428         fp = builtins.open(filename, "w+b")
   2430 try:
   2431     save_handler(self, fp, filename)

FileNotFoundError: [Errno 2] No such file or directory: 'images/aaaab.png'

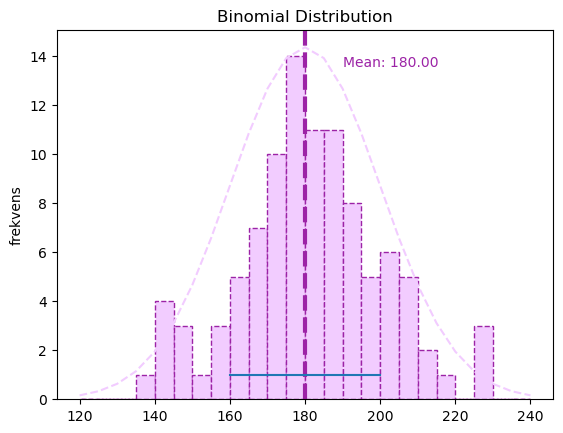
Frekvensdiagram

Regneark

abc

import matplotlib.pyplot as plt
import numpy as np

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 10000
#drawing 10000 sample from 
#binomial distribution
sample = np.random.binomial(20, 0.5, size)
bin = np.arange(0,20,1)

plt.hist(sample, bins=bin, edgecolor='blue') 
plt.title("Binomial Distribution") 
plt.show()

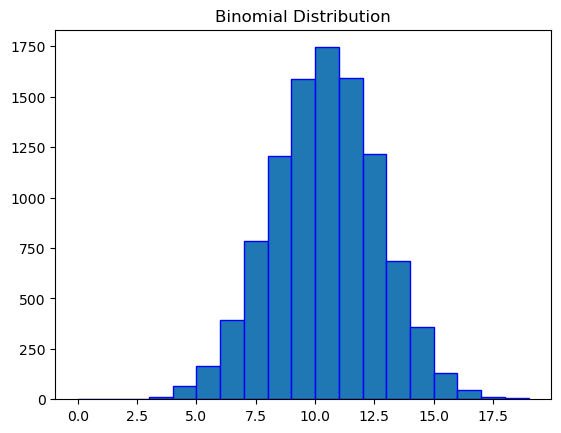
from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

sns.distplot(random.binomial(n=10, p=0.5, size=1000), hist=True, kde=False)

#sns.displot(random.binomial(n=10, p=0.5, size=1000), hist=True, kde=False)
plt.show()

C:\Users\Ellef\AppData\Local\Temp\ipykernel_17976\2958739759.py:5: UserWarning: 

`distplot` is a deprecated function and will be removed in seaborn v0.14.0.

Please adapt your code to use either `displot` (a figure-level function with
similar flexibility) or `histplot` (an axes-level function for histograms).

For a guide to updating your code to use the new functions, please see
https://gist.github.com/mwaskom/de44147ed2974457ad6372750bbe5751

  sns.distplot(random.binomial(n=10, p=0.5, size=1000), hist=True, kde=False)

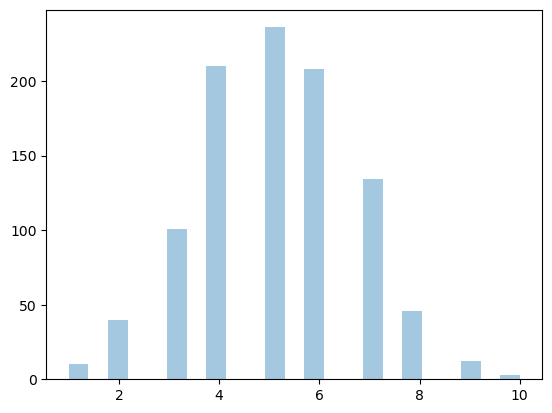
fig = pyplot.figure();
ax = fig.add_subplot(111)
ax.set_xlabel("$x$; høyere verdi mot høyre")
ax.set_ylabel("Verdi på venstre- og høyreside")

# https://stackoverflow.com/questions/4761623/how-to-change-the-color-of-the-axis-ticks-and-labels-for-a-plot-in-matplotlib
leftColour ="#32777D"
rightColour = "#44A836"
solutionColour = "#9E9B35"
#ax.xaxis.label.set_color(exponentColour)
#ax.spines['bottom'].set_color(exponentColour)
#ax.spines['bottom'].set_lw(0)
#ax.tick_params(axis='x', colors=exponentColour)
#base = 3;
xMin = -5
xMax = 5
xPoints = numpy.arange(xMin, xMax, 1)
x = numpy.arange(xMin, xMax, 0.1) 
yLeft = 2*x + 3
yRight = x**2 - 5

pyplot.title("Likning med venstreside $2x + 3$ og høyreside $x² − 5$") 


pyplot.axhline(0, color="#AAAAAA", linewidth=.5)
pyplot.axvline(0, color="#AAAAAA", linewidth=.5)


# Plot the points using matplotlib 
pyplot.plot(x, yLeft, leftColour) 
pyplot.plot(x, yRight, rightColour) 
pyplot.plot([-2,4], [-1,11], "o", color=solutionColour)
pyplot.plot([0,0], [3,-5], "x", color="#3FB336")
exponentPlot = pyplot.show()

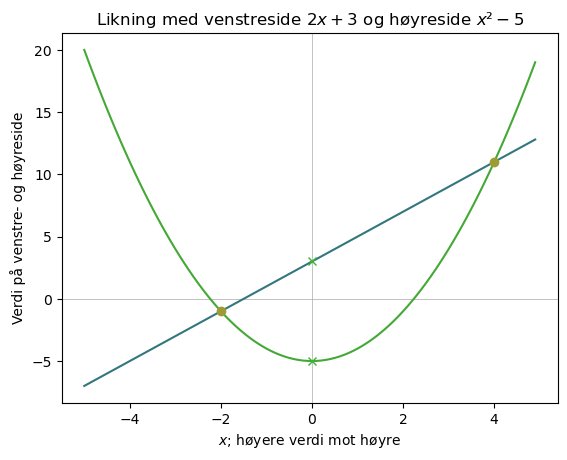
Populasjoner som bokser

Denne er videreutviklet fra (Pripp, 2017); den er eksperimentell og har ikke noen ordentlig navn.

graphvizSource(r"""digraph G{
rankdir=LR
node [shape=record fontname=Arial color="#9C23A6" fillcolor="#F2CCFF"]
edge [fontname=Arial fontsize=10 fontcolor="#9C23A6"]
populasjon [label="Populasjon\nStor|Eksempler\nNorske 8. klassinger\lAlle mulige terningkast\l|Viktig å vite:\nStørrelse\lNormalfordelt?\lStandardavvik\l" 
    style="dashed,filled" fontsize=16 ]
utvalg [label="Utvalg\nMindre|Eksempler\n100 8. klassinger\l100 terningkast\l|Viktig å vite:\nStørrelse\lNormalfordelt?\lStandardavvik\l"
    style="filled" fontsize=12]
utvalg:ne -> populasjon:nw [dir=back tailarrow=vee label="Utvalg"]
utvalg:se -> populasjon:sw [arrowhead=vee taillabel="Statistisk\nanalyse" headlabel="...si noe"]
}""")

Eksempel: En kontinuerlig parameter

La oss si vi ønsker å forske på høyden i norske 8. klassinger. Det er upraktisk å måle alle sammen, så vi måler 100 stykker. De har gjennomsnittlig høyde 179 cm. Kan vi dermed konkludere med at norske 8. klassinger har gjennomsnittlig høyde 179 cm?

Om du har god tid, og gode venner, kan du godt pause her og diskutere spørsmålet med vennene. Eller, om du er lærer, kan du be klassen diskutere dette.

Diskusjonen kan komme opp med flere poeng:

• Vi må forutsette at utvalget er tilfeldig. Det vil si at høye og lave elever har like stor sjanse for å bli utvalgt. Sagt med fagspråk: Utvelgelsen og høyde er uavhengige parametre.

• Om vi hadde valgt ut bare to eller tre 8. klassinger, ville dette vært en usikker metode. Da kunne vi hatt tilfeldig uflaks, og fått tre stykker som var lite representative. Når vi velger ut hundre stykker, derimot, kan vi være en del sikrere på at vi treffer mer nøyaktig. Jo større utvalg, jo sikrere kan vi være på at vi treffer nøyaktig. Om de utvalgte hundre elevene har høyde 179 cm, kan vi være ganske sikre på at populasjonens gjennomsnittshøyde er rundt 179 cm. Her trenger vi frekvensdiagram med normalfordelignskursve hvor disse tallene er plottet inn

• Vi vet fortsatt ikke nøyaktig hva populasjonens høyde er. Vi kan være noenlunde sikre på at den er 179±5cm (altså mellom 174 cm og 184 cm). Om vi har en større utvalgsstørrelse (1000 stykker?) kan vi være noenlunde sikre på at den er mellom 179±1cm (mellom 178 og 180 cm). Jo større utvalg, jo mer nøyaktig kan vi si noe om populasjonen.

• Med en gitt utvalgsstørrelse (f.eks. 100 elever) kan vi kanskje være 90% sikre på at populasjonens gjennomsnitt er 179±5cm og 50% sikre på at populasjonens gjennomsnitt er 179±2cm. For å regne ut de nøyaktige tallene trenger vi å vite noe om standardavvik.

Eksempel: Andre typer parametre

Tilsvarende gjelder også andre typer parametre. Vi tar med noen eksempler:

• Dikotom: Vi ønsker å forske på andelen som liker matematikk. “Å like matematikk” er dikotom (kan ha to verdier: “liker” og “ikke liker”).

• Kategorisk: Yndlingsområde Utfallsrom: {Algebra, Geometri, Sannsynlighet, Databehandling, Programmering}.

• Ordnet: Karakter. Utfallsrom er alle mulige karakterer; disse har en ordning, men har ikke nødvendigvis lik avstand (selv om mange i praksis forutsetter at det er like stor forskjell på F og E som på B og A).

• Diskret Klassetrinn. Utfallsrom er klassetrinnene. Disse har en ordning og har lik avstand; men bare visse verdier (som kan sammenliknes med heltall) finnes som utfall. Verdier som “7.25-klasse” finnes ikke.

• Kontinuerlig Høyde. Høyde er kontinuerlig (som et reelt tall; men selvfølgelig innenfor et intervall (mellom 0.5 og 4 m?)).

Eksempel: Intervensjon

Virker positiv respons? Noen ganger ønsker vi å sjekke ut om en intervensjon/tiltak/behandling fungerer. For eksempel vil vi teste “å gi mer positiv respons”. Da ønsker vi å sammenlikne virkningen med tiltaket med virkningen uten. Det er vanlig å dele inn i ett intervensjonsutvalg (også kalt “intervensjonsgruppe”) og en kontrollutvalg (også kalt “kontrollgruppe”).

Tanken er at alt er mest mulig likt i disse to gruppene unntatt intervensjonen. Gruppene bør være tilfeldig (randomisert) valgt ut fra populasjonen.

Begrep

Algoritmer