1.2.7. Innsetting

Forutsetninger og læringsmål

Dette forutsetter et variabelbegrep.

Innsetting er nyttig til svært mye i praksis og videre matematikk. Innsetting brukes for eksempel til

• Egentlig all bokstavregning

• likningsløsninger

• funksjoner

• innsettingsmetoden for likningssett

• induksjonsbevis.

Vi vil, selv om det er litt uvanlig, argumentere for at når vi snakker om å sette inn en verdi for noe (f.eks. et tall for en variabel) er det bedre å bruke tegnet ↦ enn =.

Introduksjon

Fig. 1.14 {lengde ↦ 105 m, bredde ↦ 68 m}
Wikimedia / Nielsf

Et rektangel har areal lik lengde×bredde. En fotballbane er 105 meter lang og 68 meter bred; arealet for denne fotballbanen er altså lik 105m×68m; dette kan skrives om til 7140 m².

Nå skal vi understreke et poeng som er så selvfølgelig at vi nesten ikke snakker om det: Man kan sette inn verdi for en variabel i en formel. Dette er altså å bruke eller applisere en formel.

NDLA om formelregning (av en eller annen grunn plassert i likninger)

Representasjoner

Navn

Vi kaller dette innsetting i en formel.

På engelsk sier vi substitution. «Å substitutere» betyr omtrent «å bytte ut». Det er altså litt forvirring o “inn” og “ut” mellom norsk og engelsk. «Utbytting» betyr dessverre tilfeldigvis noe litt annet.

Ord

Formelspråk

=

En del ganger brukes likhetstegnet = for innsetting. Da får vi for eksempel \(A = l×b, l = 105\mathrm{m}, b=68 \mathrm{m}\). Dette er vanlig, og matematisk ok; likevel finnes innvendinger mot denne notasjonen;

• Likhetstegnet brukes vanligvis om noe symmetrisk, “er lik”. Det ser ut som at \(l = 105 \mathrm{m}\) er en likning. Egentlig snakker vi ikke om en likning, men om en innsetting.

• Dessuten ser det ut til at de tre “likningene” er likeverdige. Selv om det er matematisk ok å tenke på dem som likeverdige, tenker vi egentlig at de to siste skal settes inn i den første. Notasjonen kan derfor forvirre elevers forståelse av hva likhetstegnet = betyr.

↦

Vi vil heller foreslå å bruke tegnet ↦ (maplet) for innsetting. Da får vi for eksempel \(A = l×b, l ↦ 105 \mathrm{m}, b↦68\mathrm{m}\). Dette uttrykker bedre hva vi faktisk mener å gjøre. En innvending er riktignok at notasjonen er sjeldnere.

Vi vil også foreslå det samme tegnet når vi kommer til likningsløsninger og innsettingsmetoden for likningssett.

Piler

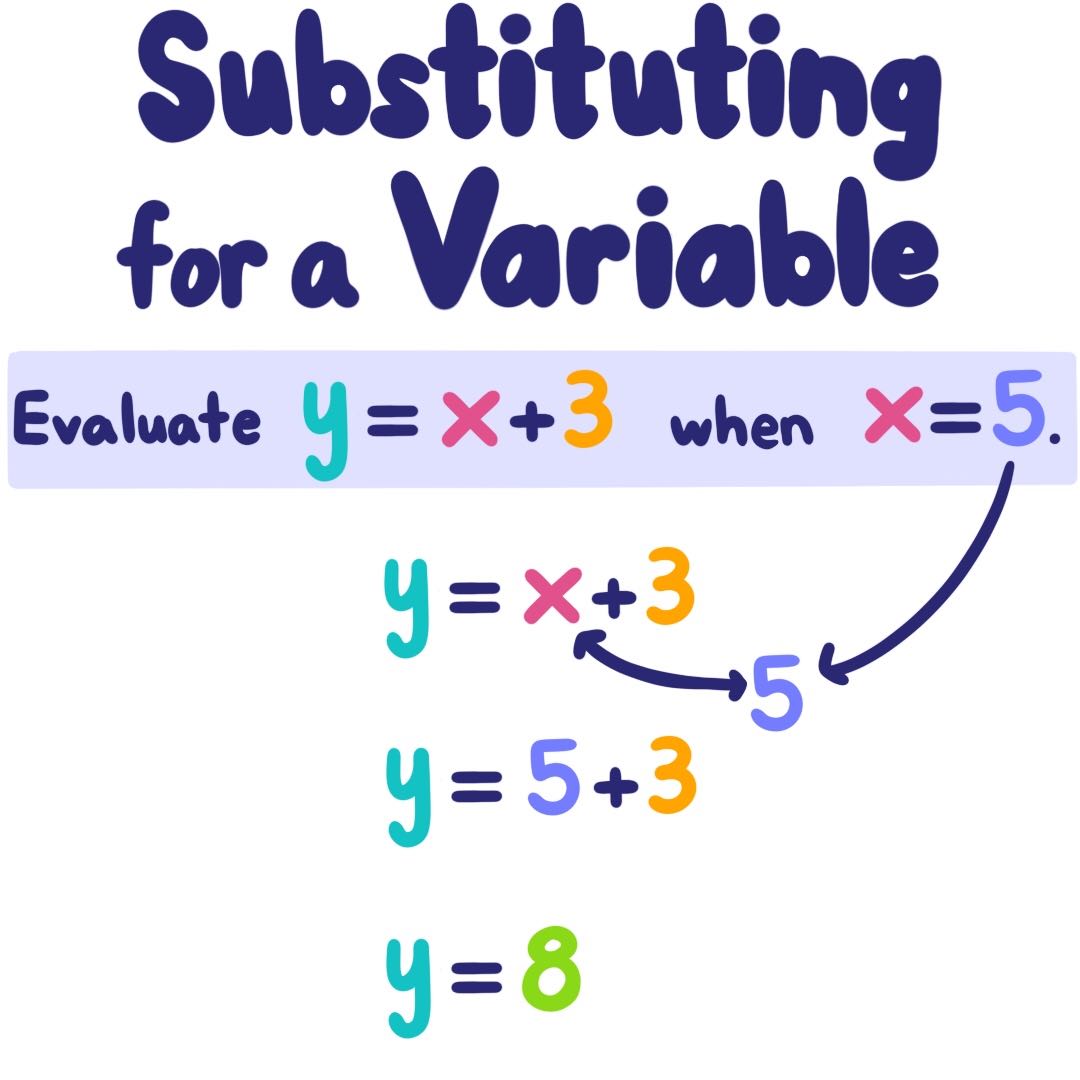
Fig. 1.15 \(y = x + 3, x ↦5\) gir \(y = 8\)
Caroline Kulczycky

Når det er teknisk enkelt å lage lange piler (f.eks. på et whiteboard) kan det være egnet å tegne opp innsetting som piler.

Andre representasjoner

Vi kan vise substituering i andre representasjoner også, men det er kanskje ikke så vanlig å vise store eksempler. Tekniske grunner? TODO

Læring

Vi bruker innsetting veldig ofte. Likevel snakker vi ikke så ofte om det.

Dette er liksom et meta-begrep som vi bare bruker og ikke snakker om. Kanskje det er fornuftig/nødvendig?