Vektorer#
Forutsetninger og læringsmål#
Introduksjon#
Rekke av tall#
Lister av tall kaller vi vektorer. I skolesammenheng møter man først vektorer med to eller tre elementer.
I følge denne definisjonen er altså en liste over årstall en vektor.
Lengde og retning#

Fig. 2.3 \(\vec{a} = AB\)#
Av en vektor kan vi regne ut en lengde og retning; mange definerer en vektor som noe som har lengde og retning i et vektorrom.
Vektorer med to elementer kan tegnes som en pil på en todimensjonal flate (et ark); vektorer med tre elementer kan tegnes som en pil i et tredimensjonalt (fysisk) rom.
Ordforklaring: Vektor
Fra latin vector (en som bærer/transporterer). Sammenlikn vehicle.
Mange fysiske størrelser (hastighet, kraft) har lengde og retning, og er altså vektorer.
Representasjoner#
Formelspråk#
En vektor kan ha et navn, f.eks. \(v\). Ofte markerer vi at \(v\) er en vektor med en pil over (\(\vec{v}\)) eller ved å sette den i tykk skrift (\(\mathbf{v}\)).
En vektor kan angies ved start- og sluttpunkt: \(AB\) eller \(\overrightarrow{AB}\).
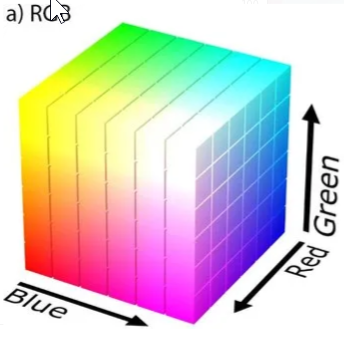
Fig. 2.4 Tredimensjonalt vektorrom#
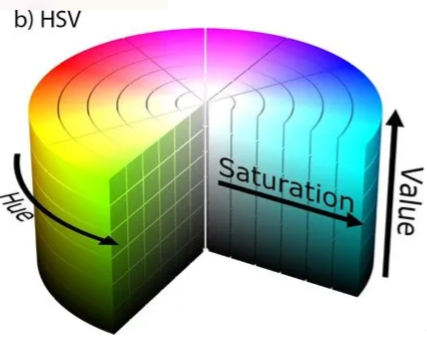
Fig. 2.5 Tredimensjonalt vektorrom#
En vektor kan angies ved sine ordinat (elementer). For eksempel kan en tredimensjonal vektor angies som \(\vec{v} = (v_1, v_2, v_3)\) eller \((v_x, v_y, v_z)\). En farge kan også angies med en vektor \((rød, grønn, blå)\) eller \((hue, saturation, lightness)\). Fargerommet er altså tredimensjonalt.
En vektor kan også representeres loddrett, særlig om den oppfattes som en n×1-matrise: \(\mathbf{v} = (v_1, v_2, v_3)^T = \begin{bmatrix}v_1\\ v_2\\ v_3 \end{bmatrix}\)
Koordinatsystem#
En vektor kan representeres som en pil i et koordinatsystem.
Dette egner seg best for vektorer med to eller tre elementer.
GeoGebra#
I GeoGebra kan punkt og vektorer angies med vanlige parenteser (v = (2,3)), med lengde og retning (v = (4; 33.7°) med semikolon mellom). GeoGebra har funksjoner for f.eks. å regne ut lengde og retning av en vektor.
Excel#
I Excel er det svært vanlig å ha loddrettte eller vannrette lister med tall. Man angir en liste ved første og siste celle med kolon mellom (f.eks. A1:C1). Svært mange funksjoner virker på lister (=sum(A1:C1)).
Søylediagram#
Vi har allerede tall-linje-representasjoner for tall. En naturlig representasjon for liste av tall er å ha flere slike under hverandre, eventuelt å vri dem og ha dem etter hverandre. Da får vi noe som likner veldig på søylediagram!
Dette representasjonsspråket er godt egnet for vektorer med mange elementer.
Algoritmer#
Lengde#
Tenk Pythagoras. Lengde \(|\mathbf{v} | = \sqrt{v_1^2 + v_2^2 + v_3^2}\)
Addisjon og subtraksjon#
Like lange vektorer kan adderes ved å addere tilsvarende elementer. Blir kommutativt.
Multiplikasjon#
Litt mer komplisert; Faktisk to typer multiplikasjon.
Statistikk#
Statistikk har mange operatorer som virker på lister av tall, f.eks. “gjennomsnitt”.
Aspekter#
Rekke av tall
Lengde og retning
