Den assosiative lov

Forutsetninger og læringsmål

Vi snakker om den assosiative lov for addisjon: \(\overset{a + (b + c)}{\underset{(a + b) + c}{⇵}}\) og \(\overset{a × (b × c)}{\underset{(a × b) × c}{⇵}}\).

• 2. klasse: utforske den kommutative og den assosiative egenskapen ved addisjon og bruke dette i hoderegning
• 3. klasse: bruke kommutative, assosiative og distributive egenskaper til å utforske og beskrive strategier i multiplikasjon

Denne siden handler om den assosiative lov for addisjon og multiplikasjon. Vi skal senere snakke generelt om assosiativitet for andre operatorer.

Introduksjon fra addisjon

Assosiativ lov

Vi skal nå introdusere en ny lov, men en som ikke gjelder for subtraksjon.

Assosiativ lov for addisjon

For addisjon har vi at 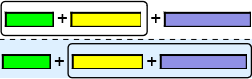\(\overset{(a + b) + c}{\underset{a + (b + c)}{⇵}}\). Derfor sløyfer vi ofte parentesen helt, og skriver bare a + b + c. Dette kalles den assosiative lov for addisjon. Den kan vises greit med småsteinrepresentasjon: Uansett hvilke tre ting vi snakker om er det likegyldig om vi først adderer de to første og så adderer resultatet med det tredje — eller om vi først adderer de to siste og så adderer dette resultatet med det første.

• (2 + 3) + 4 = .

• Sveriges befolkning + (Norges befolkning + Danmarks befolkning) ? er lik er ikke lik (Sveriges befolkning + Norges befolkning) + Danmarks befolkning (altså det skjedde ikke noen befolkningsendring ved overgangen i 1814). Denne sammenhengen kalles ? den kommutative lov den assosiative lov den distributive lov veitrafikkloven loven om at gjetting noen ganger går bra for addisjon.

Representasjoner

Om vi har gode representasjoner er assosiative lover mer eller mindre selvfølgelige. Det kan man egentlig si om de fleste lover og algoritmer. Med dårlige representasjoner er de kronglete.

Småstein

Læring

TODO