Felles nevner

Forutsetninger og læringsmål

Læringsmål

Du skal kunne finne felles nevner til to brøker.

Dette brukes både til sammenlikning og addisjon.

Referanser

Phet har bl.a. simuleringer, aktiviteter og læringsressurser om brøksammenlikning

Introduksjon

Representasjoner

Steinbit

Steinbit i kryss (flis)

Ord

Felles nevner og minste felles nevner

Formelspråk

Vi vil finne felles nevner mellom \(\frac{t_1}{n_1}\) og \(\frac{t_2}{n_2}\)

Småstein og fliser

Tømmerstokk

Algoritmer

Samme nevner

Når to brøker har samme nevner, er dette selvfølgelig den felles nevneren vi er ute etter. \(\frac{6}{17}\) og \(\frac{5}{17}\) har felles nevner 17.

Multiplisere nevnerne

Den enkleste algoritmen for å finne felles nevner er å multiplisere nevnerne! Felles nevner mellom \(\frac{1}{2}\) og \(\frac{1}{3}\) er \(\frac{}{6}\). Dette er ikke alltid den minste mulige felles nevner, men den er alltid en mulig felles nevner.

Dette er, for de aller fleste elever, den beste algoritmen.

De tilfellene de to nevnerne har en felles faktor \(f\), vil produktet av nevnerne bli \(f\) ganger så stor som den minste mulige felles nevneren.

Minste felles multiplum

Å finne felles nevner er å finne (minste) felles multiplum. Tømmerstokk

Grafisk i kryss

Tegner den ene brøken den ene veien og den andre andre veien og teller.

= multiplisere teller og multiplisere nevnerne

Fordel: Peker videre mot multiplikasjon etc.

Faktorisere

Denne algoritmen har vært vanlig før. Den er imidlertid komplisert og har vanligvis få fordeler; jeg vil derfor sjelden anbefale den.

Nerder og flinke studenter som leser dette likevel, kan likevel glede seg over at den gir innsikt i faktorisering og mengdelære. Dessuten finnes det situasjoner utenfor skolen hvor det er en praktisk fordel å ha små tall.

Algoritmen er slik: Vi faktoriserer begge nevnerne. Unionen av de to faktorene En variant

TODO eksempel?

En felles nevner mellom to brøker \(\frac{a}{b}\) og \(\frac{c}{d}\) er en som inneholder alle faktorene til både \(b\) og \(d\). Den enkleste måten å finne et tall som inneholder alle faktorene er å multiplisere dem. En mulig felles nevner blir derfor produktet av nevnerne: \(bd\).

La oss for eksempel si vi skal sammenlikne ⅔ og ⅕. ⅔ kan representeres . ⅕ kan representeres , men også . Akkurat nå interesserer vi oss bare for nevnerne (de tynne strekene), ikke for tellerne (det fargelagte området). Vi er interessert i produktet av tellerne. Vi skal multiplisere og . Uten begrunnelse foreslår vi nå at det gir mening å sette dem i kryss akkurat som når vi multipliserer ellers:
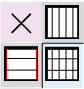. Den felles nevneren blir antall delområder i , altså 15.