1.1.5. Telle og tall#
Forutsetninger og læringsmål#
Læringsmål#
Du skal kunne telle. Du skal også kjenne småsteinrepresentasjonen for tall.
Du skal kjenne begrepene representasjon og algoritme.
Hvorfor bruker vi tid på dette?#
Lesere av dette (for eksempel lærerstudenter GLU1 på NLA) kan telle til ti. Hvorfor bruker vi tid på dette?
Vi bruker tid for å introdusere en del begrep vi skal ha nytte av senere. Blant disse er representasjon og algoritme. Vi skal også bruke første uke på å introdusere gode arbeidsmåter. Blant dem er å gjøre . Din oppgave er her å bytte ut oransje med grønn.
Når vi kan noe så godt at det er automatisert, er de kanskje vanskelig å sette seg inn i situasjonen for dem som mangler automatisering. Hva tenker en elev når han ser 
? Eller når hun ser 3 + 5?
Læreplanen#
Referanser#
(Hinna et al, 2016) 1.3side51 (Kardinaltall, ordinaltall, identifikasjon etc)
(Pind, 2011) Naturlige tall s47
(Valenta, 2016d: Tallforståelse - anvendelse og engasjement)
Introduksjon#
Olav, Håkon, Anne og Helene sitter i stua. Vi skal hente en sjokolade til hver av dem på kjøkkenet. Hvor mange sjokolader skal vi hente? Svaret er .
Når vi skal gå ut og hente sjokolader, er det praktisk å huske på et tall i stedet for å huske på alle navnene. Så lenge det er få personer, kan vi nok huske alle navnene når vi går ut på kjøkkenet; men om vi hadde flere personer ville det fort bli upraktisk. Det er enklere å huske på .
Representasjoner#
"The best and most beautiful things in the world cannot be seen or even touched — they must be felt with the heart.
Helen Keller
Barn lærer at ordet “fire” og fire fingre strukket ut betyr det samme. Andre representasjoner for det samme er “🍏🍏🍏🍏” og “4”. Det finnes også mange andre, for eksempel “four”, “四”, “”, “IIII” og “Ⅳ”. Vi kan tenke oss at dette er forskjellige representasjoner for samme matematiske objekt.
Representasjoner er essensielt for læring. Det gjelder kanskje spesielt i matematikk, hvor vi ikke kan se eller ta på objektene vi snakker om (Duval, 2006). Vi må ha representasjoner både for å snakke med andre om matematikk og for å tenke selv. Vi kan bare tenke på objektene gjennom representasjoner, for vi kan jo ikke ta på eller se objektene (for eksempel tallene). Dette er en forskjell på matematikk og mange andre fag.
Kanskje læres først representasjoner som “3”, ⚂, 
og “tre” hver for seg, utifra eksempler, og kan senere vokse sammen til ett konsept.
Tellbar mengde (småstein)#
Representasjonene “🍏🍏🍏🍏”, “IIII” og “” likner på hverandre. Det eneste forskjellig er hvilken type elementer (epler, streker og 
er.). Vi har en mengde elementer som kan telles. Slike representasjoner kalles gjerne tellbare mengde-representasjoner.
Oppgaver:
🍏🍏🍏 = .
5 =
I praksis skal vi tegne småsteinene som enklere objekter, for eksempel røde firkanter. Tallet (som ellers kan representeres med 5) vil vi tegne som 
.
Ordforklaring: Calculus
En ting som er egnet til telling er småstein. En liten stein heter på gammelgresk χάλιξ (khálix). Dette blir på latin kalx. Diminutiv-(liten-form-)endelsen -ulus gir at en calculus er en liten småstein. Kanskje den første matematikken ble utviklet på stranda?
Abakus#
Teknologier er ofte forbundet med representasjoner. En gammel teknologi for telling er abakus (telleramme).
Småstein og andre konkreter#
En “teknologi” som er veldig brukbar i undervisning er konkreter: Fysiske objekter som representerer matematikk. Et eksempel er småstein (altså virkelige, fysiske småstein). Et annet er et målebånd som likner en tall-linje.
Representasjoner: Sifre#
Representasjonen “4” er helt annerledes. Tegnet “4” (og ordet “fire”) må pugges, og kan neppe forståes. For små barn er “4” like fremmed som “四”.
Vi må ikke tenke at “4” er tallet; strengt tatt er “4” bare én representasjon blant mange mulige. Riktignok er det ofte praktisk å si «tallet 4» heller enn «tallet som er representert av “4”».
Sifre er kanskje vanskelig å forstå; men de er raske å skrive og jobbe med. Det går raskere å skrive “9” enn å tegne 9 epler. Dette gjelder særlig når vi utvider siffer-systemet til desimalsystemet; det går raskere å skrive “999” enn å tegne 999 epler (eller 9 eplepappesker, 9 eplebrett og 9 enkeltepler). Så når vi først har lært sifrene bruker vi det gjerne.
En lærer må vite forskjell på begrepene siffer og tall. Tallet 23 inneholder to sifre. En lærer må alle finne på å si at «23 inneholder to tall»!
Ord#
Lyder, senere bokstaver. Tallrekka TODO
Representasjonsspråk#
Vi har introdusert representasjoner av flere typer: Eplerepresentasjoner, firkantrepresentasjoner, ord og sifre. Vi kan snakke om et eple-representasjonsspråk, et firkantspråk, ord-språk og sifferspråk. Det vi her kaller språk kalles også metaforer, representasjonstyper, representasjonssystem og registre (Duval, 1998?). Et viktig språk (eller språkfamilie?) er tellbar mengde.
Vi kan neppe tenke eller kommunisere mye matematikk uten slike språk. Læring av slike språk er derfor essensielt. Vi skal understreke at matematikk må formuleres gjennom språk.
Representasjonsspråk kan brukes til å representere litt forskjellige typer tall. Tellbare mengder kan representere positive heltall. Sifre kan representere bare tall fra 0 til 9. “Terning-representasjonen” (hvor for eksempel “⚄” representerer det samme som “5”) kan representere bare tallene mellom 1 og 6 (altså mellom ⚀ og ⚅).
Vi skal senere introdusere mange forskjellige representasjonsspråk, for eksempel
tall-linje-språket, hvor
representeres ved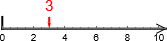 
. Dette kan representere både desimaltall og negative tall!desimalsystemet, en utvidelse av siffer-språket; dette kan representere heltall større enn 9 (og mye mer)
utvidelser av tellbar mengde som kan representere addisjon
, brøk 
og mye mer.
Å lære et representasjonsspråk#
Representasjoner må læres. Det kan gjøres på to måter (Lakoff & Nunez, 2000) p.53:
Grunnleggende metaforer har en likhet med det de skal representere. Eksempler er tellbar mengde. Disse kan læres utifra eksempler.
Påbyggingsmetaforer må læres gjennom andre metaforer. Vi har da et kjent språk og et ukjent (Høines, 1998: Begynneropplæringen). En måte å gjøre det på er oversettelsesoppgaver. Elevene får en representasjon i ett språk som skal oversettes til representasjon av samme objekt i et annet språk. Eksempel:
🍏🍏🍏 = .
5 = .
2 = .
Slike oppgaver har ikke noen egentlig regning, bare oversettelse mellom representasjoner.
Algoritmer#
En algoritme er en ting vi kan gjøre med tall (eller andre matematiske objekt) og som gir et tall (eller annet matematisk objekt). Eksempler er å legge sammen, å gange og å doble.
Et annet ord er prosedyre.
Telle#
Skal vi finne et tall, kan vi telle. Å telle er en algoritme (prosedyre). Et barn kan telle ved å fokusere på hver person én gang mens hun nevner tallordene i rekkefølge; det siste tallordet angir antallet i hele mengden.
Et barn som skal lære å telle må altså kjenne rekka av tallordene (“en, to, tre, fire…”) først.
Vi kan telle en mengde og få et naturlig tall.
La oss tegne sjokolader som brune firkanter 
. Da kan vi skrive
Brune firkanter representerer altså en mengde sjokolader. Røde firkanter representerer nå et tall. Vi kan tegne
Foreløpig snakker vi bare om de tallene som kommer av telling. Disse kalles naturlige tall eller telletall. Senere skal vi også introdusere andre typer tall, for eksempel desimaltall.
Telle opp#
En motsatt algoritme er når vi har et tall, og skal telle opp (eller “plukke ut”?) et antall sjokolader. Vi skal altså gå fra et tall til en mengde.
Begrepet telle opp er mindre vanlig enn telle i matematiske tekster. Sånn vi bruker ordene her, betyr telle å gå fra en mengde til et tall, mens telle opp betyr å gå fra et tall til en mengde.
Subitisering (automatisering)#
Et barn vil raskt telle mengder som . Når barnet har møtt samme bildet noen ganger, vil det uten å telle kunne identifisere antallet. Dette skjer svært raskt for tall opp til 7±2 (Miller, 1956). Dette kalles subitisering. Slik “hurtig-telling” foregår muligens på egne steder i hodet.
### Å lære en algoritme Å lære en algoritme kan vi for eksempel lære ved å herme etter en ekspert (f.eks. en lærer på tavla) som utfører algoritmen.
En god representasjon gjør algoritmer naturlig. For eksempel er det naturlig i representasjonen “
” hvordan man skal telle, men kanskje vanskeligere i “7”. Senere skal vi se at noen representasjoner (f.eks. småstein) også gjør for eksempel addisjon naturlig.
Talltyper#
Naturlige tall#
Vi snakker nå om telletall. Dette er positive heltall. I matematikken kalles disse naturlige tall og har symbolet ℕ.
Kardinaltall og ordinaltall#
Dette er ikke ferdig; delvis fordi det er mest aktuelt for tidlig barneskole.
Didaktikk#
Barns utvikling
Tallrekke uten mening
Tallrekke
Algoritmen telle TODO
Gjerne tension, algoritme, mål
Gjerne situasjon, eksempel, representasjon
Matematikkhistorie#
TODO fra Qed?
Filosofi#
TODO: Vi kan tro at tallet representert ved 4 eksisterer, men fremtredende fremtredende didaktikere og filosofer mener at vi ikke kan være sikre på det (TODO Lakoff & Nũnez, Sfard, ¿Derrida, Strukturalistene). Vi kan bare se representasjonene! Vi tenker oss at dette er representasjoner av samme begrep. Dette begrepet kan vi ikke ta på, men vi kan tro at det er der. #Platon #Huleliknelsen #Saussure #Peirce. Sfard (??) ønsker å unngå termen “representasjon” fordi den forutsetter noe ontologisk. Contra vil vil argumentere for at det er rasjonelt å anta at det vi representerer som 3 finnes i en virkelighet. Vi antar dette ved Tro #Paulus. TOrbjørns videoer:
TODO: