1.1.9. Deling#

Forutsetninger og læringsmål#

Vi skal introdusere divisjon (deling) i to tankemodeller. Vi skal også introdusere en ny talltype — rasjonale tall.

Graph

Læreplan#

Referanser#

Introduksjon: Dele og måle#

Vi har to tankemodeller for 15÷3. De er knyttet til verbene dele og måle:

  • Wiggo har 15 roser han vil dele likt i tre buketter. Hvor mange roser får vi i hver bukett??
    Dette er eksempel på delingsdivisjon:
    🌹🌹🌹🌹🌹     🌹🌹🌹🌹🌹     🌹🌹🌹🌹🌹

  • Wiggo har 15 roser han vil dele i buketter med tre roser hver. Hvor mange buketter får han?
    Dette er eksempel på målingsdivisjon:
    🌹🌹🌹    🌹🌹🌹    🌹🌹🌹    🌹🌹🌹    🌹🌹🌹

Tankemodeller#

Du husker kanskje vi hadde to tankemodeller for subtraksjon: Fjerne-subtraksjon og forskjell-subtraksjon. Disse har lik formel (\(a - b\)), men forskjellig verb og forskjellige representasjoner både som småstein og på tall-linje..

På samme måte har vi to forskjellige tankemodeller for divisjon. De har felles formel, men forskjellige verb, regnefortellinger, småstein-/flisrepresentasjoner og tall-linje-representasjoner.

Delingsdivisjon#

I delingsdivisjon \(\overset{a÷b}{\underset{c}{↓}}\) deler vi opp a i b antall grupper, og c er hvor mange det er i hver gruppe.

Eksempel er altså 🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹 delt på grupper (buketter) gir 🌹🌹🌹🌹🌹.

a og b er av samme type (f.eks. roser). Navnet har å gjøre med at vi deler opp a.

Målingsdivisjon#

I målingsdivisjon \(\overset{a÷b}{\underset{c}{↓}}\) deler vi opp a i grupper som er b, og så blir c antallet grupper.

Eksempel er altså 🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹 delt på grupper 🌹🌹🌹 så antallet grupper blir .

a og b er har samme enhet (f.eks. roser). Navnet har å gjøre med at vi måler oppover til a og ser hvor mange grupper vi har fått da.

Representasjoner#

(Klaveness et al, 2019) 85s328

Småstein#

Vi har allerede representert divisjon i “rosespråket”. I småsteinspråket blir får vi mye av det samme. Det er noen ganger nyttig å framheve hva som er grupper: Det skal vi gjøre med fargen .

Tallet 15 tegner vi vanligvis , men nå skal vi tegne det .

Delingsdivisjon#

delt i grupper er         .

Vi kan tegne gruppene tydeligere og si at
delt i grupper blir .

Hver gruppe er 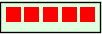det vil si .

Målingsdivisjon#

delt i grupper som er så store som 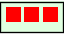blir .

Antallet grupper blir altså .

Fliser#

Divisjon i flismetaforen kan virke komplisert; vi tar det likevel med siden vi senere skal bruke det for å illustrere både kvadratrot, faktorisering og andre ting.

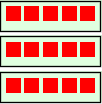Du husker kanskje at 3×5 som blir . Dette er altså tre grupper ganger fem. Vi kan tegne det i repetert addisjon: Vi kan stable via til fliser .

Delingsdivisjon#

Vårt eksempel er altså at 15÷3 blir 5. Dette er altså 15 som skal deles i tre grupper: .

Dette kan vi også stable via til .

Vi kan også sette opp divisoren, som er antall rader, til høyre: .

Svaret “faller” da ned som antall kolonner .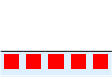

I divisjon er det kvotienten som er svaret, så vi tegner det nederst med bakgrunn . Vi velger å tegne divisor til høyre for dividend, siden det tilsvarer rekkefølgen i språket (“femten delt på tre”) og formelspråket (“15÷3”).

Endelig: Hele divisjonsstykket 15÷3 kan altså tegnes som

Det viser seg at denne representasjonen også håndterer større tall. Senere skal vi se at den også håndterer brøk, variable og andre ting. Nedenfor skal vi se at dette gir opphav til en god delingsalgoritme. For nå setter vi bare opp eksemplene
156÷12 og
156÷6 .
I begge tilfeller setter vi opp dividenden og divisoren øverst, og kvotienten faller ned på bunnlinja. I tilfellet 156÷6 må en hundrer veksles i tiere.

Målingsdivisjon#

Vårt eksempel er at 15 skal deles i grupper på størrelse 3. Vi kan også nå stable gruppene da får vi
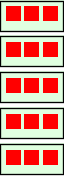. En naturlig representasjon av 15 målingsdelt på 3 er altså
.

Radene er fortsatt gruppene. Vi ser at dividenden fortsatt er øverst til venstre; divisoren er derimot nå nederst (med samme bakgrunnsfarge), mens svaret nå er antall grupper, som kommer til høyre (med bakgrunnsfargen vi bruker til svar).

Ord#

Ordforklaring: Divisjon og deling

Ordene divisjon og deling betyr det samme. Siden dividere kommer fra latin og dele “bare” kommer fra germansk, oppfatter oppfatter noen at det første høres finere og mer skriftlig ut.

Operandene kalles dividend (“blir dividert”) og divisor (“den som dividerer”). Disse ordene kommer kanskje fra delingsdivisjon? Resultatet kalles kvotient. Ordet betyr nærmest “hvor mange ganger”, og kommer kanskje fra målingsdivisjon? Vi har altså at dividend ÷ divisor = kvotient.

På norsk snakker vi altså om delingsdivisjon og målingsdivisjon. På engelsk brukes ofte sharing og measurement.

Formelspråk#

Når vi skal dele a med b, skriver vi a÷b eller a:b. De to symbolene betyr nøyaktig det samme, men har hver sine fordeler. Kolon-tegnet kan ha andre betydninger (hva betyr 23:59:59?). Tegnet ÷ ser kanskje mest profesjonelt ut, men kan være vanskelig å skrive effektivt inn uten god programvare (som f.eks. WinCompose).

Senere skal vi se at delestykket a÷b er til forveksling lik brøken a/b, men i noen tilfeller kan det være nyttig å skille mellom begrepene divisjon og brøk. Både filosofisk og pedagogisk bør vi holde forskjell på “to dividert med tre” og “to tredeler”.

Tall-linje#

15 på en tall-linje er
, eller avstanden fra 0 til dette punktet
.

Delingsdivisjon#

I delingsdivisjon skal vi dele dette i tre deler. Vi får
, altså at hver del er like lang som
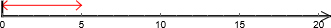. Dette er oppdeling.

Målingsdivisjon#

I målingsdivisjon skal vi dele dette opp i deler med gitt størrelse, nemlig
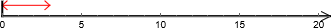. Vi kan telle oppover og se hvor mange “hopp” vi får plass til. Det blir fem hopp
.

Tall-linje-språket ga oss ikke mye nytt foreløpig; men vi skal bruke den mer seinere. En variant er “tømmerstokk-språket”, hvor en langtømmerstokk skal deles i korte stubber.

Algoritmer#

(Klaveness & Karlsen & Kverndokken, 2019) 86s330 og 87s332

Automatisering#

Også i divisjon blir vi vant til en del enkle delinge, så mye at vi kan snakke om en “divisjonstabell”. Kanskje vi for eksempel vet helt automatisk at 10÷5 er .

Løser du følgende med automatisering?

  • 20÷2 →

  • 4÷2 →

Fordele litt og litt#

Hva gjør et barn når det skal fordele 639 kroner på 3? Kanskje først deler 600 på tre (og har 39 igjen), så deler 30 på tre (og har 9 igjen), og så deler 9 på tre. Dette kan vi sette opp i en tabell:

../../_images/divisionAnimated.gif

Fig. 1.2 Divisjonsalgoritme. 639 kroner skal fordeles på 3. Barna velger å fordele 300 kr først.#

\(\begin{array}{rrrl} \textrm{Rest fordeling} & \textrm{fordeling nå} & \textrm{resultat}\\\hline 639 & 600 & 200 & \textrm{Første runde: Vi deler 600 av de 639 på 3, får 200}\\ 39 & 30 & 10 & \textrm{Andre runde: Vi har 39 igjen, deler 30 av dem på 3, får 10}\\ 9 & 9 & 3\\\hline \textrm{Sum} & 639 &213 & \textrm{Vi har i sum delt 639 og fått 213 til svar.} \end{array}\)

Vi kan legge merke til at dette kan gjøres i flere eller færre runder. Det er for eksempel ikke noe krav om at vi deler 600 i første runde. Kanskje en forsiktig elev ville dele i flere runder:

\(\begin{array}{rrrl} \textrm{Rest fordeling} & \textrm{fordeling nå} & \textrm{resultat}\\\hline 639 & \mathbf{300} & 100 \\ 339 & 300 & 100\\ 39 & 30 & 10 \\ 9 & 9 & 3\\\hline \textrm{Sum} & 639 &213 \end{array}\)

Noen ganger er eksempelet mer komplisert. La oss se på eksempelet 156÷12. En elev velger kanskje å fordele 120 først, så \(\begin{array}{rrrl} \textrm{Rest fordeling} & \textrm{fordeling nå} & \textrm{resultat}\\\hline 156 & 120 & 10 \\ 36 & 12 & 1\\ 24 & 24 & 2\\\hline \textrm{Sum} & 156 & 13 \end{array}\)

Algoritmen tilsvarer at vi i flis-språket setter opp divisoren til høyre. Så fordeler vi dividenden kolonnevis: Først fordeler vi 120 i venstre kolonne, så 12 til i neste og så 24 i de to radene lengst til høyre

.
Svaret blir .

En matematiker kan komme til å tenke på den distributive lov.

Løs for eksempel med tabell som over:

  • 2024÷4 →

  • 1236÷12 →

  • 1236÷3 →

  • 1852÷4 →

Legg merke til at når vi løser slike oppgaver gjør vi mange små automatiserte divisjoner inni. Derfor er automatisering av divisjoner som 24÷4, 20÷4, 36÷12 etc. viktige som grunnlag for divisjonsalgoritmer.

Overgang til rutenett#

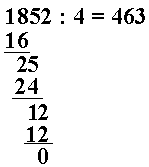
../../_images/divisionTraditional.gif

Fig. 1.3 Tradisjonell rutenettsalgoritme fra matematikk.org#

Når vi har en algoritme som den over, er det kort vei til en av de tradisjonelle rutenett-algoritmene. Slike algoritmer var vanlige før, men er etter Ellefs syn noe av det minst nyttige man kan lære på ungdomsskolen. Et eksempel er vist til høyre.

På engelsk heter dette “long division”, og noen ganger kan man også lese “lang divisjon” på norsk.

Når divisjonen ikke går opp#

Wiggo har 16 roser han vil dele likt i tre buketter. Hvor mange roser får vi i hver bukett?

Om vi kan dele roser får vi 5+⅓ roser i hver bukett. Men å dele roser er ikke særlig romantisk. Vi kan si at det blir en til overs. Mer om dette i eget dokument om delelighet.

a÷1#

Om vi “deler” noe på en gruppe, får personen like mye som var til fordeling. Vi har at \(\overset{a ÷ 1}{\underset{a}{⇵}}\).

Oppgave

  • 452/1 →

Sammenheng med multiplikasjon#

Vi har tidligere påpekt at 3×5 blir 15, mens 15÷3 blir 5. Dette gjelder for alle tall unntatt 0: \(\overset{a×b → c}{\underset{c÷b → a}{⇵}}\).

Derav følger også at \(\overset{a÷b → c}{\underset{a÷c → b}{⇵}}\). Dette blir ofte formulert som en likningsregel: \(\overset{a÷b = c}{\underset{a÷c = b}{⇵}}\)

Repetert subtraksjon#

Noen sammenlikner målingsdivisjon med repetert subtraksjon.

Negative tall#

Her gjelder loven “minus og pluss blir minus, mens minus og minus blir pluss”. Vi har at

  • Et positivt tall delt på et positivt tall er positivt , sammenlikn multiplikasjon

  • Et positivt tall delt på et negativt tall er negativt , sammenlikn multiplikasjon

  • Et negativt tall delt på et positivt tall er negativt , sammenlikn multiplikasjon

  • Et negativt tall delt på et negativt tall er positivt , sammenlikn multiplikasjon

Talltype#

Man kan subtrahere to heltall. Da kan man få et svar som ikke er helt — et rasjonalt tall (brøktall)! Divisjon åpner altså en ny talltype!

Læring#

Cambridge espresso “Division and multiplication”

Misoppfatninger: