Samle (forkorte) brøk

Samle (forkorte) brøk#

Forutsetninger og læringsmål#

Læringsmål#

Du skal kunne

Samle en brøk
Avgjøre når en brøk ikke kan samles mer

8. klasse: utforske og beskrive primtallsfaktorisering og bruke det i brøkregning. Primtallsfaktorisering er relevant når vi skal samle brøk.

Hensikt#

Det er ofte praktisk å jobbe med brøker som har så små tellere og nevnere som mulig. Bedre enn \(\frac{22}{88}\) er \(\frac{2}{8}\), eller \(\frac{1}{4}\): Da blir det også enkelere å forstå hva vi snakker om.
Sist, og ikke minst: Matematikklærere krever ofte at svar på matematikkstykker er ferdig samlet. \(\frac{2}{8}\) gir ikke fullt poeng.

Vi har nå snakket om brøker hvor teller og nevner er heltall. Det aller meste gjelder også for “brøker” hvor teller og nevner er bokstavuttrykk eller brøker (brudne brøker).

Introduksjon#

Vi har tidligere snakket om å utvide brøker. Å samle dem er det motsatte: Å gå fra til .

Å samle er litt vanskeligere enn å splitte; for når vi skal samle må vi finne hvilken faktor vi kan samle med. Vi kan samle brøken med faktoren 2; Men hvordan finner vi faktoren?

Representasjoner#

Ord#

Denne operasjonen blir tradisjonelt kalt forkorting, selv om ingenting blir kortere. Vi skal kalle den samling, fordi områdene blir samlet (seksdeler blir samlet til tredeler).

Vi sier at vi samler en brøk med en faktor: Når vi samler \(\frac{10}{15}\) til \(\frac{2}{3}\) samler vi med 5. Vi deler altså teller og nevner på faktoren 5. Dette kan vi gjøre fordi 5 var faktor i både teller og nevner i \(\frac{10}{15}\).

Det vi her kaller samle kalles ofte forkorte. Hva blir kortere? Kanskje listen over faktorer?

Småstein og fliser#

Eksempel 10/15

Formelspråk#

Vi kan formulere regelen \(\overset{\frac{a·faktor}{b·faktor}}{\underset{\frac{a}{b}}{↓}}\). I siste eksempel var felles faktor 5. Det vanskelige er å finne denne felles faktoren.

Lister med faktorer#

I formelspråket er det nyttig å se at telleren og nevneren i en brøk kan skrives som lister av faktorer. \(\frac{210}{495}\) kan skrives som \(\frac{2·3·5·7}{3·3·5·11}\), fordi 210 kan faktoriseres til 2·3·5·7 og 495 kan faktoriseres til 3·3·5·11.

Dele på det samme over og under#

Vi skal utvikle algoritmer som ender med regelen: Å samle er å dele teller og nevner på samme faktor.

Forkorting-graf#

Vi tar også med en litt eksperimentell representasjon av samling. Om denne er vanskelig, så hopp over, men den kan også gi innsikt.

Algoritmer#

Se muligheter for forkorting#

Først vil vi nevne en litt usystematisk algoritme, som kanskje er vanlig. Den går ut på å se enkle muligheter og forkorte ettersom man ser mulighetene. Så stopper man når teller eller nevner er primtall eller innbyrdes prim (altså at man ikke kan forkorte mer).

La oss si man har brøken \(\frac{84}{132}\). Vi ser kanskje ikke hva dette kan forkortes til. Men

Vi ser kanskje at begge tallene er partall og altså har faktor 2. Forkorter vi med 2 får vi \(\frac{42}{66}\).
Dette ble også partall; forkorter vi en gang til får vi \(\frac{21}{33}\). Nå er ikke 2 felles faktor lengre,
men 3 er: Forkorter vi med 3, får vi \(\frac{7}{11}\), som er primtall.

En litt mer systematisk variant er å prøve ut de små primtallene (2,3,5,7,11,13) etter tur. Man kommer ofte langt med de tre første, som også passer bra til hoderegning.

Faktorisere teller og nevner og dele på felles faktor#

En mer systematisk algoritme er denne:

Man primtallsfaktoriserer teller og nevner.
Man finner hvilke faktorer som finnes i både teller og nevner. Dette er felles faktor(er), og om man har primtallsfaktorisert ha man største felles faktor.
Man samler med felles faktor. Om man samler med største felles faktor har man samlet så mye det går an.

I eksempelet \(\frac{84}{132}\) er største felles faktor 2×2×3; det er disse faktorene vi forkortet med etter tur.

La oss også se på eksempelet \(\frac{210}{495}\). Vi kan primtallsfaktorisere begge tallene, så vi ser at vi har \(\frac{2·3·5·7}{3·3·5·11}\). En felles faktor er 3·5, som blir 15. Vi kan altså dele teller og nevner på 15 og få \(\frac{210÷15}{495÷15}\). En snarvei her er å bare fjerne 3·5 fra listene over faktorer \(\frac{2·\color{LightGray}3·\color{LightGray}5·7}{3·\color{LightGray}3·\color{LightGray}5·11}\) (å fjerne 3·5 fra listen over faktorer er det samme som å dele på 3·5). Da står vi igjen med \(\frac{2·7}{3·11}\) som er \(\frac{14}{33}\). \(\frac{210}{495}\) er altså \(\frac{14}{33}\).

Det er helt greit om noen vil samle med bare 5 (og få \(\frac{2·3·7}{3·3·11}\) altså \(\frac{42}{99}\)); denne brøken kan så samles videre ved å fjerne felles faktor 3 så vi kommer til \(\frac{14}{33}\). Det er også greit om noen først vil samle med bare 3 (og få \(\frac{2·5·7}{3·5·11}\) altså \(\frac{70}{165}\)); denne kan samles videre med å fjerne felles faktor 5. I alle tilfeller får vi samme svar.

Grafiske representasjoner#

I steinbit-, bløtkake- og tall-linje-representasjoner er det vel ikke veldig lett å se hvilke faktorer vi kan samle med.

I steinbit-representasjoner kunne man kanskje prøve på "å legge i rektangel", men jeg har ikke fått det til å bli veldig elegant.

Vet vi hva vi skal samle med, kan vi i prinsippet dele teller og nevner på det samme TODO. I
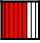(altså \(\frac{6}{9}\)) kan vi dele både telleren og nevneren på 3. Da får vi også
.

Digitale verktøy#

Om man skriver inn en brøk (f.eks. \(\frac{10}{15}\)) på en kalkulator, i et regneark eller i Python får man en avrundet desimalverdi: 0.33…. Andre digitale verktøy (f.eks. Wolfram Alpha eller Python-pakker som fractions behandler relle tall eksakt; disse vil altså forkorte så mye som mulig, men ikke runde av \(\frac{1}{3}\) til 0.33.

\(\frac{a}{1}\)#

En brøk på a en-deler kan bli til a. er det samme som .

Vi har at \(\overset{\frac{a}{1}}{\underset{a}{⇵}}\).

\(\frac{a}{a}\)#

En brøk på a a-deler blir til 1. kan samles til som i følge regelen over er .

Vi har at \(\overset{\frac{a}{a}}{\underset{1}{⇵}}\), og også at \(\overset{\frac{na}{a}}{\underset{n}{⇵}}\)

Når er en brøk ferdig samlet?#

Hvordan vet vi at vi ikke kan samle en brøk mer?

Det korte svaret er: Når teller og nevner ikke har felles faktorer.

Når teller eller nevner er forskjellige primtall vet vi at brøken ikke kan samles mer. \(\frac{5}{14}\) kan ikke samles mer.

Når teller og nevner er innbyrdes primtall, altså ikke har flere felles faktorer, kan de heller ikke samles mer. \(\frac{4}{9}\) kan ikke samles.

Didaktikk#

Mange øvede matematikklæree ser automatisk at en brøk med felles faktor 2, 5 eller 10 kan samles. Dette er ikke så selvfølgelig for elever!

Annet#

Det er kanskje overraskende at vi uansett kommer til samme brøk til slutt. Det viser seg at for enhver brøk finnes det en unik brøk hvor man ikke kan forkorte mer. Da har teller og nevner ingen felles faktorer. Dette kan vises utifra det vi kalte aritmetikkens fundamentalsetning: Alle naturlige tall har en unik primtallsfaktorisering.