Primtall

Forutsetninger og læringsmål

Primtall bygger på faktorisering og multiplikasjon. Det brukes videre i brøkregning, særlig når vi skal samle brøker.

• 8. klasse: utforske og beskrive primtallsfaktorisering og bruke det i brøkregning

Cambridge Espresso: “Factors, multiples and prime numbers”

Hvorfor bryr vi oss om primtall?

Primtall kan føles ganske virkelighetsfjernt, både for elever og studenter. Grunnen til at vi introduserer dette allerede nå er at vi trenger noen teknikker i det videre arbeidet med brøk. Selv om primtall ikke lenger er sentralt for å finne minste felles multiplum, er de sentralt for å samle (forkorte) brøker.

Introduksjon

Fig. 1.6 Fra Wikimedia / David Eppstein

Primtall er tall som ikke kan faktoriseres. De kan altså ikke legges i rektangel (bortsett fra rektangel hvor den ene sida er 1 eller -1). Et tall som kan faktoriseres kalles noen ganger et sammensatt (composite) tall. Ordet “sammensatt” bygger på metaforen at å faktorisere er å dele opp, mens et primtall er udelelig.

Representasjoner

Ord

Å primtallsfaktorisere er å faktorisere til det bare er primtall igjen. Når det er bare primtall igjen kan vi ikke faktorisere mer. For 132 er 2×2×3×11 en primtallsfaktorisering, mens 2×2×33 ikke er det; 33 kan faktoriseres videre og er ikke primtall.

Algoritmer

Hvilke faktorer må vi sjekke

≤√a

La oss si vi skal faktorisere et tall a, f.eks. 139. Hvor mange mulige faktorer må vi sjekke?

Tallet må ha to faktorer som vi kan kalle f₁ og f₂. Vi har at a = f₁f₂. Om f₁ = f₂ vil de være lik √a; om en av dem er høyere må den andre være mindre. Derfor må minst en av faktorene være ≤√a.

Vi vet kanskje ikke kvadratroten til 139, men vi vet kanskje kvadratroten til 144; det er 12. Kvadratroten til 139 må være litt mindre. Om 139 har faktorer må minst én av dem være <12. Skal vi sjekke faktorer til 139, trenger vi bare sjekke kandidater opp til 12! Dette sparer enormt mye arbeid.

Sjekke bare primtall

Det er også sånn at vi bare trenger sjekke faktor-kandidater som er primtall. Det er enklere å sjekke om 2 er faktor enn at 4 er det; og om vi vet at 2 ikke er faktor et vi at heller ikke 4 kan være det.

Hvorfor? Om 4 var en faktor i tallet, ville også 2 være det. Dette er eksempel på motsigelsesbevis: \(\overset{P ⇒ Q}{\underset{¬Q ⇒ ¬P}{⇵}}\) hvor P er “4 er faktor” mens Q er “2 er faktor”.

Algoritmer for å primtallsfaktorisere

Å faktorisere flere ganger

Vi har faktorisert 132 til faktorene 12 og 11 . Men 12 kan faktoriseres videre til 3 og 4 og 4 kan igjen faktoriseres videre til 2 og 2 . Vi kan sette opp dette:

Mange lager en tabell for dette, for eksempel
\(\begin{array}{rrrl} \textrm{Rest faktorisering} & \textrm{faktor nå} & \textrm{resultat}\\\hline 132 & 2 & 132100 \\ 339 & 300 & 100\\ 39 & 30 & 10 \\ 9 & 9 & 3\\\hline \textrm{Sum} & 639 &213 \end{array}\)

Prøve seg fram

Når vi primtallsfaktoriserer kan vi prøve ut mulige faktorer. Hver gang vi finner en faktor, skriver vi opp den, trekker den ut av tallet (ved å dele på faktoren) og prøver videre helt til vi ikke finner flere faktorer.

Automatisering

Automatisering av enkelttilfeller spiller en rolle også her. Skoleelever bør lære seg å faktorisere de minste kvadrattallene, 6, 8, 12 osv. Noen av oss har faktorisert 132, 144 og 156 så mange ganger at vi kan svaret.

En systematisk algoritme

Her er en systematisk algoritme. Den er relativt enkel å utføre, gitt at du har skjønt avsnittene over; men den er litt kronglete å beskrive. Vi begynner derfor med et eksempel (🪓140):

\(\begin{array}{rlr} \textrm{Rest faktorisering} & \textrm{faktor nå} & \textrm{resultat}\\\hline 140 & 2 & 70 \\ 70 & 2 & 35\\ 35 & 2 \textrm{ går ikke} & 35\\ 35 & 3 \textrm{ går ikke} & 35\\ 35 & 5 & 7\\ 35 & 5 \textrm{ går ikke} & 7\\ 7 & 7 & 1 \end{array}\)

Vi sjekker altså alle primtallene (2,3,5,7,…) etter tur, de laveste først, om de er faktor. Vi begynner altså med 2; om dette er en faktor i 140, trekker vi faktoren ut og skriver i høyre kolonne. 2 kan være faktor flere ganger, så vi sjekker en gang til; 2 er faktor også i 70, så vi skriver 35 i høyre kolonne. Men nå er ikke 2 faktor mer. Da sjekker vi neste tall faktor-kandidat (3). 3 er ikke faktor i 35 (og derfor ikke i 140). Da sjekker vi 5, som viser seg å være faktor. Derfor skriver vi 7 i høyre kolonne. (På dette tidspunktet kunne vi observert at 7 er primtall og derfor ikke kan faktoriseres mer, så vi kunne egentlig stoppet). Vi sjekker om 5 er faktor flere ganger (nei) og om 7 er faktor (ja). Faktorene i 140 står nå i mitre kolonne: 2, 2, 5 og 7.

Det finnes mange varianter av dette oppsette; for eksempel vil mange kutte ut høyre kolonne.

Eratosthenes’ sil

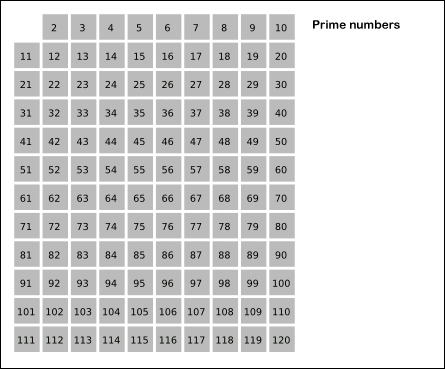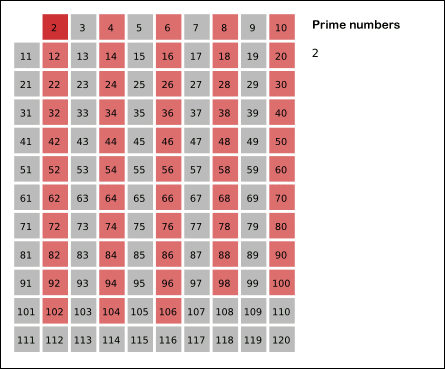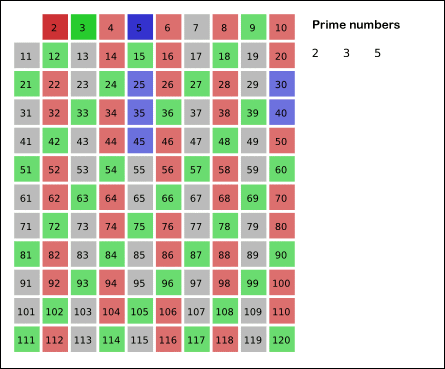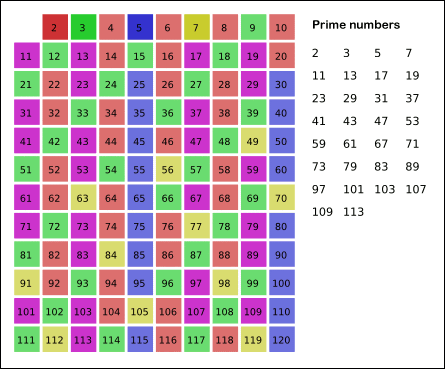
Fig. 1.7 Erastothenes’ sil (fra Wikimedia)

Grunnide: Må skrives bedre: Ha en tabell over de første naturlige tall. For hvert primtall du finner (først 2, så 3, …) krysser du vekk alle multipler av tallet. Når du har funnet 2 krysser du for eksempel bort 2,4 og alle andre partall. Når et tall ikke er krysset vekk er det et primtall.

Definisjon på Eratosthenes’ sil

Eratosthenes’ sil er effektiv, iallfall på moderate tall.

Primtallsfaktoriseringen er unik

Det viser seg merkelig nok at det er bare én måte å primtallsfaktorisere et gitt naturlig tall. 132, for eksempel, har bare én primtallsfaktorisering (2×2×3×13). Vi regner da med at faktorenes orden er uviktig: 13×2×2×3 blir regnet som samme faktorisering som 2×2×3×13.

Det er imidlertid flere måter å komme til faktoriseringen på: Skal vi faktorisere 132 kunne vi begynt med 2×66. Om vi fortsatte å faktorisere ville vi likevel komme til samme primtallsfaktorisering. Her er et eksempel hvor jeg trekker ut de minste primtallene først (se algoritme nedenfor)

Dette resultatet er så viktig for matematikknerder at det blir kalt aritmetikkens fundamentalteorem. Det ble bevist av Euklid rundt år −300.