Prosenttall, brøk og desimaltall#
Forutsetninger og læringsmål#
Du skal kunne regne om fra hvilken som helst av tallformene prosenttall, brøk og desimaltall til hvilken som helst annen tallform..
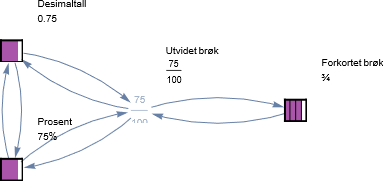
Siden formene har lik verdi kan vi regne om fra én til en annen. Elevene må kunne regne om flere veier. Dette kan vi sette opp i oversikten under:
Introduksjon#
Tallformer: Brøk, prosenttall og desimaltall#
Tall kan altså skrives som
Brøk
 \(\frac{75}{100}\), \(\frac{75}{100}\) eller forkortet brøk
\(\frac{75}{100}\), \(\frac{75}{100}\) eller forkortet brøk  \(\frac{3}{4}\)
\(\frac{3}{4}\)Prosenttall
 , \(75\;\%\)
, \(75\;\%\)Desimaltall (som vi riktignok ikke har introdusert ennå)
 , \(0.75\)
, \(0.75\)
Testoppgaver#
Vi skal kommentere noen av disse overgangene spesielt; men for å sjekke hva du kan kan du prøve å fylle ut følgende tabell allerede nå. Noen er kanskje enkle, men minst én er litt vanskeligere:
Desimaltall |
Prosent |
Brøk, \(\frac{}{100}\) |
Brøk, forkortet |
|---|---|---|---|
|
|
|
|
|
% |
||
|
|||
% |
\(\frac{10}{100}\) |
||
% |
|
TODO bilder
Representasjoner#
Algoritmer#
Algoritmer mellom prosent og brøk#
Prosent til brøk#
Prosent til uforkortet brøk er enkelt. “Prosent” betyr jo “hundredel”. Vi bytter bare ut “prosent” med “hundredel”. 20%  = 20/100. Så kan vi bare forkorte brøken. Vi kan velge å først forkorte den til /10, og mest forkortet versjon er $1,$2.
= 20/100. Så kan vi bare forkorte brøken. Vi kan velge å først forkorte den til /10, og mest forkortet versjon er $1,$2.
Noen kaller dette å dele på 100%. 100% er jo lik 1, og vi kan alltid dele på 1 og få samme tallet. Vi kan slå sammen (forkorte) prosent-tegnet i teller og nevner. \(130\% = \frac{130\%}{1} = \frac{130\%}{100\%} = \frac{130}{100} = \frac{13}{10}\). Vi må derimot ikke si “å dele på 100”. Hvorfor skulle det plutselig være lov til å dele på 100? Dette ville bare bli en spesialregel som ikke henger sammen med matematisk logikk ellers. Likevel finnes det matematikklærere som sier til elever at “i prosentregning må du dele på 100”. Det riktige er “…dele på 100 prosent”.
Sammentrukket kan vi si at \(\overset{rp\\\%}{\underset{r\frac{p}{100}}{⇵}}\).
Brøk til prosent#
Å regne om fra brøk til prosent er bare litt vanskeligere. Vi har altså en brøk \(\frac{teller}{nevner}\) og vil prøve å utvide den til å få 100 som nevner \(\frac{p}{100}\). Det finnes flere måter å tenke på, og elevene kan med fordel tenke selv.
Om elevene vet hva en likning er, kan de bruke det: \(\frac{teller}{nevner} = \frac{p}{100} = p\%\). Vi skal finne \(p\), og får \(p = \frac{100·teller}{nevner}\). Har vi brøken ¾, blir altså p lik \(\frac{100·3}{4}\); dette kan forkortes til \(\frac{25·3}{4}\) og til 75. ¾ går altså til 75%.
Elevene kan også velge å regne ut verdien av brøken som desimaltall. Denne inni-algoritmen bruker divisjon. ¾ = 0.75. Resultatet kan så multipliseres med 100%: 0.75·100% = 75%.
I ganske mange tilfeller kan det også lønne seg å splitte (utvide) brøken til tideler eller hundredeler. Dette gjelder for eksempel når man har todeler eller femdeler. ⅖ = \(\frac{4}{10}\) som da enkelt kan utvides til \(\frac{40}{100}\) og 40%.
Sammentrukket kan vi si at \(\overset{r\frac{t}{n}}{\underset{r\frac{t·100\%}{n}}{⇵}}\)
½ er lik %.
⅘ er lik %.
⅓ er lik % (avrundet til heltall).
⅔ er lik % (avrundet til heltall; litt vanskelig avrunding?).
Algoritmer mellom prosent og desimaltall#
Dette avsnittet forutsetter kjennskap til desimaltall, som vi strengt tatt ikke har introdusert ennå.
Prosent til desimaltall#
Å regne om fra prosent til desimaltall er ikke veldig vanskelig. 125% betyr for eksempel 125 hundredeler, som vi kan regne ut som et divisjonsstykke. Her er altså divisjon en inni-algoritme.
40% er lik .
230% er lik .
Oppmerksomme elever (og studenter) vil skjønne at vi alltid kan “flytte kommaet to plasser”. Dette er en bra snarvei; som vanlig er vi redd for at snarveier kan bli brukt som magi uten at eleven skjønner hvorfor. Vi kan gjerne utfordre tenkende elever til å fundere på hvorfor det alltid er greit å “flytte kommaet to plasser samtidig som vi fjerner prosent-tegnet”.
30% er lik .
3012% er lik .
Vi kan også snakke om “å dele på 100%”, som altså er å dele på .
Vi kunne også snakke om å “gå veien om brøk”.
Desimaltall til prosent#
Å regne fra desimaltall til prosent kan vil gjøre med å gange med 100% (som altså er å dele på ). 0.17·100% blir da %. Vi gjentar at vi ganger med .
Også her er det lov til å tenke at vi “flytter kommaet to ganger samtidig som vi legger til prosenttegn”.
0.5 er lik % (om en elev svarer 5% her: Hva har hen tenkt?).
0.175 er lik % (om en elev svarer 175% her: Hva har hen tenkt?).
30 er lik % (om en elev svarer 0.3% her: Hva har hen tenkt?).
101 er lik %.
Andre tallformer: Promille og ppm#
Noen ganger ser man også promille, som betyr “per tusen”. Det har tegnet ‰. 10‰ er altså lik %. Snakker vi om 0.5‰ i forbindelse med alkohol, betyr det at alkohol utgjør 0.5% av blodets volum.
Ordet ppm står for “parts per million” og betyr milliondeler. På det tidspunktet samfunnet begynte å snakke om slike konsentrasjoner, hadde verden tydeligvis begynt å snakke engelsk heller enn latin og italiensk. CO₂-konsentrasjonen i atmosfæren har økt fra 280 ppm i 1850 til 420 ppm i 220. 420 ppm tilsvarer altså ‰ og %.
Filosofi#
Tallformer#
Vi kan diskutere filosofisk om dette er forskjellige former av samme tall eller det er tall som er like (eller «likeverdige») hverandre. I dette dokumentet vil vi kalle dem tallformer og være enige om at formene har lik verdi.
Aspekter ved prosent#
Man kan snakke om ulike aspekt ved brøk: Brøk som tallverdi, brøk som del av helhet, brøk som operator, brøk som divisjon, brøk som måling og brøk som forhold. Tilsvarende kan man snakke om om aspekter ved prosent. Noen ganger møter man også påstander om at brøk eller prosent “i virkeligheten er” ett av aspektene.
Ulike representasjoner antyder muligens forskjellige aspekter: kanskje tall-linja antyder brøk som tallverdi, mens andre antyder brøk som forhold mellom andre tall. Ord som “halv(parten)” antyder kanskje at noe er halvparten av en helhet.
Også andre tall kan ha forskjellige aspekter. Ordet “dobbelt” antyder kanskje forhold, i og med at man er dobbelt av noe.
I vår matematiske tradisjon er det kanskje vanligst å forbinde heltall med tellbar mengde, brøk som forhold og prosent som del av en helhet.


 0.5
0.5 35%
35% 3/2 TODO
3/2 TODO er lik
er lik  er lik
er lik  er lik
er lik