1.5.11. Argumenter

Forutsetninger og læringsmål

Vi har lært mye om matematiske objekt, særlig arimetikken og algebraen. Så har vi lært om påstander om objekt. Vi har også snakket om regler som kan brukes til å skrive om påstandene til nye påstander. Nå skal vi lære om å argumentere for reglene og påstandene.

Læreplanen

Resonnering og argumentasjon er faktisk et av kjerneelementene i LK20.

For innføring, se (Hovik & Solem, 2021).

Introduksjon

Det finnes konkrete argument (f.eks. at det er sol i dag eller at 2 + 3 er lik 3 + 2); men de fleste argumentene vi snakker om er generelle (at det er sol om sommeren eller at a + b = b + a).

Språk i argument

Felles for alle argument er at de har et språk. Det kan for eksempel være

• Formelspråket

• Tall-linje, flis-språk eller et annet grafisk språk

• Et eksempel, som også kan representere noe mer generelt

• Naturlig språk (norsk eller engelsk)

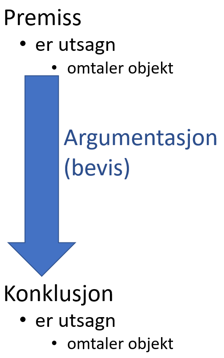
Premiss og konklusjon

Argumentasjon bygger svært ofte på noen premiss. Dette er påstander som blir forutsatt; konklusjonen er sann om premissene er sanne.

En argumentasjon kan sånn sett sammenliknes med en implikasjon ⇒. Den kan brukes som en regel \(\overset{}{\underset{}{↓}}\)

Et gyldig argument argumenterer sannhetsverdien til en konklusjon (om premissene er sanne, da).

Oppgave:

1. Om premissene er sanne må da konklusjonen være sann?

2. Om premissene er usanne må da konklusjonen være usann?

3. Om konklusjonen er sann, må da premisset være sant?

4. Om konklusjonen er usann, må da premisset være usant?

Løsning

1. Ja, det har vi akkurat sagt (for et gyldig argument, da)

2. Nei. Eksempel: La oss si at vi har en gyldig argumentasjon med premiss “det regner” og konklusjon “det er vått på bakken”. Da kan det likevel tenkes at det ikke regner men likevel er vått på bakken.

3. Nei, jmf. eksempelet i forrige punkt

4. Ja, faktisk; kontrakfaktisk bevis. En situasjon hvor konklusjonen er usann og premisset er sant ville stride mot argumentasjonen.

Table 1.13 Sannhet og gyldighet

	Påstand	Argument
Ja	Sann	Gyldig
Nei	Usann	Ugyldig
Engelsk	Valid	Invalid
	Hva er sant?	Hva kan vi vite?
Fag	Ontologi	Epistemologi

Sannhet og gyldighet

Mens en påstand kan være sann eller usann kan et argument være gyldig eller ugyldig.
Gyldig betyr her “om premissene er sant må konklusjonen være sann”.

Eksempler

Eksempler på argument kan være

• Utregning, f.eks. løsning av likninger

• Formelle bevis bygget på regler

• Vitenskapelige artikler (og masteroppgaver)

• Politiske argument…?

• Eksempler utenfor matematikk

Typer argumentasjon: “Nivå av argumentasjon”

En inndeling av argumentasjon kalles gjerne “nivå av argumentasjon”:

• 👩‍🏫 Referanse til autoriteter (f.eks. lærer eller lærebok)

• 🌷 Bevis fra eksempler (empiriske bevis)

• ❀ Handlinger i representasjonsspråk (generiske eksempler): Handling som blir vist i et konkret eksempel, men hvor det er klart at handlingen kan gjøres i alle tilfeller

• ⤓ Regelbasert deduksjon

Generalitet

Noen bevis er for noe relativt konkret (f.eks. at 5 + 0 er 5). Andre er mer generelle (f.eks. at \(a + 0 → a\))

Mange bevis er på formen “For alle naturlige tall n, så er P sant om n” (altså {rule}`∀ n ∈ ℕ, P(n)’.

(Lannin, 2005) mener “generalization” og “justification” hører uløselig sammen.

Representasjoner

Vi snakker her om representasjoner av selve beviset; vi kan også snakke om representasjoner av det som blir bevist.

Det er mange representasjoner under nivåene, særlig under deduktiv argumentasjon

Navn

Litteraturen (og dagligtale) bruker ordene bevis, argument og resonnement litt forskjellig. Noen mener bare de aller sterkeste argumentene fortjener å bli kalt bevis; altså at bevis er sikkert. Andre bruker bevis videre, også for litt svakere argumentasjon.

(Reid & Knipping, 2010), kapittel 7, gir opp og bruker ordene “bevis” og “argumentasjon” om hverandre.

(Stylianides, 2007), side 291, mener bevis har følgende egenskaper:

• Det bruker påstander akseptert av en gruppe (community); disse blir antatt uten videre begrunnelse. Dette er definisjoner, aksiomer, teorem etc.

• Det bruker argumentasjonsmåter som er kjent og akseptert av gruppa. Dette kan være regler.

• Det er kommunisert ved representasjoner kjent av gruppa. Dette er representasjoner, enten språklige, fysiske eller andre. Han mener altså at et bevis er noe som fungerer i en gruppe.

Noen skiller mellom “argumentasjon” som handling og “argument” som det ferdige produktet, omtrent som vi kan skille mellom “regningen” eller “bevisføringen” som handling og (den ferdige) “utregningen” og “beviset” som det ferdige produktet.

Retning

Ofte tenker vi at bevis går nedover eller mot høyre. Men en ordbruk som “bygger på” eller “i bunn ligger” antyder at vi tenker oss at beviset bygges oppover.

Grafiske representasjoner også for bevis?

Argumentasjon har mindre utviklet tradisjon for grafiske representasjoner enn likninger har. Grafisk representasjoner av likninger har blitt vanligere og mer standardisert for bare få tiår siden; vi kan håpe at grafiske representasjoner for argumenter følger etter.

Algoritmer

Se også om de forskjellige nivåene, særlig under deduktive bevis: Der står det bl.a. om å finne bevis.

Presentere bevis

Presenterer du et argument som bygger på handlinger i et representasjonsspråk? Generisk eksempel? Setter du sammen en argumentasjonsrekke fra premiss til konklusjon som bruker eksisterende regler?

Kan du representere strukturen i beviset grafisk (f.eks. med piler)? Bruker du induksjon? Kontrapositivt? Ad absurdum? Uttømming?

Kan du representere det du beviser om grafisk (f.eks. representere partall med par av prikker)?

Men kanskje viktigst: Presentere hvordan man kan bruke bevis i undervisning

Bruke bevis i undervisning

Dette er hva dere skal gjøre som lærere.

Når man skal undervise om noe: Bruke bevis

Ofte er det gitt hva man skal undervise om og hva som er målet. Da kan man spørre: Kan jeg bruke bevisteknikker til å nå dette målet?

Når man skal presentere må man ha klart for seg hvem man presenterer til. Hva er forkunnskapene? Motivasjonen?

Man må også ha klart for seg sitt mål. Målet er sannsynligvis knyttet til kompetansebegrepet. Eksempler: Er målet

• bare at tilhørerne (elevene) til å tro på en konklusjon eller ny regel?

• at elevene skal huske konklusjonen eller en ny regel?

• å lære et nytt begrep? Å generalisere noe de tidligere kan?

• å lære et nytt representasjonsspråk?

• å lære noe om bevis?

Hvor mye skal elevene oppdage selv, og hvor mye skal de få servert? Får de servert noen språk å bygge på? Regler?

Hvilke undervisningsaktiviteter bruker man? Forklaring? Oppgaveløsing? Annet?

Aspekt

Argument ≠ årsak!

Argument er ikke det samme som årsak! Se om ordet hvorfor.

Læring

Det er vanlig at elever (og studenter!) blander påstander (f.eks. likninger) med argument. For eksempel blander de sannhet med gyldighet.

Men…

Vi har snakket om argument om påstander. Kan vi ikke også ha argument om f.eks. bokstavuttrykk?

Kan argument bli påstander? Kan argument bli objekt?

Er konstruksjonen \(x -1 = 2 ⇒ x = 3\) et argument eller en påstand?