Avhengige parametre (betinget sannsynlighet)#

Forutsetninger og læringsmål#

Vi skal nå snakke om at to parametre kan være uavhengige eller avhengige (betinget av hverandre).

Referanser#

  • {{referanse(“qed 5-10 bind 1”, “7.7 s798 Betinget sannsynlighet”)}}

Referanser#

Læreplan #

Annet#

Introduksjon#

Eksempler#

Terningkast med to terninger ⚅⚅#

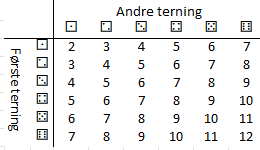
Krysstabell med summen av de to terningene

Vi skal jobbe med kast med to terninger, og se hva de blir tilsammen. ⚂ og ⚃ blir tilsammen 7. Utfallsrommet er i figuren satt opp i en kryssrepresentasjon (med summen i cellene).

Vi skal bruke dette som eksempel på to uavhengige parametre (utfallet av det ene terningkastet påvirker ikke utfallet av det andre).

Hår- og skofarge 👟#

Sko- og hårfarge i en populasjon
I tabellen over terningene var cellene fylt med summer (2‒12). Vi kan også lage en krysstabell og fylle cellene med frekvenser. I eksempelet til høyre har to personer lyst hår og hvite sko. Figuren har tatt med noen summer med grå skrift, selv om du kunne regnet ut dette selv.

Representasjoner#

Utfallsrom med utheving av gunstige utfall og mulige utfall#

Hendelsen “≥5 gitt ≥ 3”
Hva er sannsynligheten for å få minst fem, om vi vet at vi har minst tre?

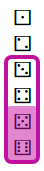
De gunstige utfallene er her {⚃, ⚄}. Hele utfallsrommet er {⚀, ⚁‚ ⚂, ⚃, ⚄, ⚅}. Men det er gitt at vi har fått minst tre. Vi må snakke om rommet av mulige utfall: {⚂, ⚃, ⚄, ⚅}.

Begrepet “rommet av mulige utfall” er ikke vanlig, men jeg oppfatter det som veldig brukbart.. Det er mulig vi trenger et bedre ord. Deltotal? Aktuell-total?

Representasjonen til høyre er ikke vanlig, men jeg oppfatter den som god. Den har bare status som eksperiment.

Sannsynligheten for å få minst fem gitt at vi får minst tre er som vanlig \(\frac{\textrm{Størrelsen på rommet av gunstige utfall}}{\textrm{Størrelsen på rommet av mulige utfall}}\). Her blir det \(\frac{2}{4}\).

Ord for betinget sannsynlighet#

Vi kan altså snakke om sannsynligheten for en hendelse gitt en annen (for eksempel sannsynligheten for å få ≥5 gitt ≥3). Vi kan også snakke om utfallene som gir minst fem blant dem som gir minst tre.

Den andre hendelsen er en betingelse.

På engelsk (kjekt å vite til søking, f.eks. etter bilder) snakker vi om “condition” og “conditional probability”.

Formelspråk#

Hendelsen A gitt B kan skrives A|B; den loddrette streken kan leses “gitt”.

| kan leses som en operator som tar to hendelser (A og B) og gir en ny (A|B)

Vi skriver også ofte tegnet ¬ for “ikke”.

Krysstabell#

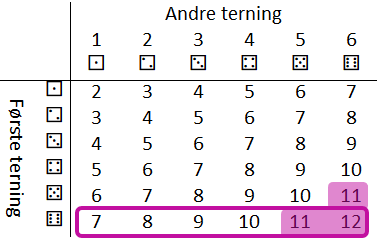
Sannsynlighet for å få 11 eller 12 gitt at første er ⚅
Hva er sjansen for å få tilsammen minst 11 om første terning er ⚅?

Vi kan tegne opp dette i en krysstabell og framheve både rommet av gunstige utfall og rommet av de mulige utfall.

Vi ser at det er to gyldige utfall som er innenfor rommet av mulige utfall, av seks mulige utfall.

\(P(\textrm{sum} ≥5 | \textrm{første} = ⚅) = \frac{2}{6}\).

QEDfig44s782

Krysstabell med frekvenser#

Hva er sjansen for hvite sko gitt lyst hår?

$P(\textrm{hvit} | \textrm{lyst}) = \frac{2}{3}$

Til høyre står en krysstabell med frekvenser, med utheving av rommene av gunstige og mulige utfall. Vi ser at sjansen for hvite sko blant dem som har lyst hår (altså \(P(\textrm{hvit} | \textrm{lyst})\)) er \(\frac{2}{3} → 67\%\).

Men Hva er sjansen for hvite sko blant dem som ikke har lyst hår? Dette er to av syv, altså \(\frac{2}{7}→29\%\).

Vi ser at sannsynligheten for hvite sko er mye større blant dem som har lyst hår. Vi sier at hendelsene lyst og hvit er avhengige av hverandre. Når hvit er avhengig av lyst, er også lyst avhengig av hvit.

Begrep#

Uavhengige hendelser#

Vi skal foreløpig forutsette at de to terningene er uavhengige. Det vil si at hva vi får på den første påvirker ikke den andre.

QEDs781

Vi kan også snakke om “uavhengige parametre”.

Digitale verkøty#

Algoritmer#

Sjekke om to parametre er uavhengige#

  • Teoretisk / fornuftig: Det er teoretisk/fysisk/kulturelt plausibelt at to terningkast er uavhengige.

  • Empirisk: ** Sjekke om \(P(A|B) = P(A|¬B)\)

Lover#

\(P(A \textrm{ og } B)\): Produktsetningen#

Ved uavhengige hendelser#

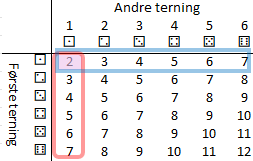
Multiplikasjon (gitt uavhengighet)
Hva er sjansen for å få ⚀ på begge terningene? Hva er altså sjansen for å få ⚀ på første terning og å få ⚀ på andre også?

Vi antar at terningkastene er uavhengige. Er det følgende forståelig?Vi kan da tenke oss at utfallsrommene for hvert av terningene er multiplisert med hverandre, som i flismetaforen. Sammenlikn dette med flisrepresentasjon av ⅙×⅙ TODO. Resultatet likner veldig på en krysstabell.

I figuren til høyre er rommet hvor første terning er ⚀ markert med blått og rommet hvor andre terning er ⚀ markert med rødt. Rommet av det (ene) gunstige utfallet ⚀⚀ har lilla bakgrunn. Vi ser at \(\frac{1}{36}\) av utfallene er gunstige, fordi \(\frac{1}{6}×\frac{1}{6} = \frac{1}{36}\).

En mulig begrunnelse multipliserer kanskje tellerne for seg og nevnerne for seg: 1×1 = 1 og 6×6=36.

Generelt har vi, for uavhengige hendelser, at \(P(A ∧ B) = P(A) × P(B)\). (tegnet ∧ betyr “og”).

A og B kan også være hendelser med mer enn ett utfall. Sjansen for å få ⚂, ⚃, ⚄ eller ⚅ på minst én av terningene = \(\frac{4}{6} × \frac{4}{6} → \frac{4}{9}\).

Multiplikasjon (×), og (∧), snitt (∩) og “begge” har med hverandre å gjøre.

QED 7.4.1s773. Se illustrasjon i en slags flismetafor fig4 s.782

Ved avhengige hendelser#

Produkt av sannsynligheter
Hva er sjansen for at en person har lyst hår og hvite sko? Vi spør altså etter sannsynligheten for at en person har lyst hår ∧ hvite sko (som er noe annet enn summen av sannsynligheten for (unionen av) alle som har lyst hår eller hvite sko).

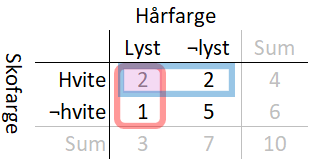
Vi kan se av tabellen at to av ti personer (20%) har lyst hår og hvite sko. Det er noe annet enn sannsynligheten for lyst hår (\(\frac{3}{10}\)) ganger sannsynligheten for hvite sko (\(\frac{4}{10}\)) (12%). Formelen \(P(A ∧ B) = P(A) × P(B)\) gjelder altså ikke når vi har avhengige hendelser.

Dette må forklares bedre, har ikke tid nå

  • Sjansen for at en person i denne populasjonen har lyst hår og hvite sko er lik sjansen for lyst hår ganger sjansen for at en som har lyst hår har hvite sko.
  • Sjansen for at en person har lyst hår og hvite sko (2/10) er lik sjansne for lyst hår (3/10) ganger sjansen for hvite sko gitt lyst hår (2/3).
  • $P(lyst ∧ hvite) = P(lyst)×P(hvite|lyst)$.

QEDsetning3 s782

QED 7.7s798 “betinget sannsynlighet”

ndla om produktsetningen

Bayes lov#

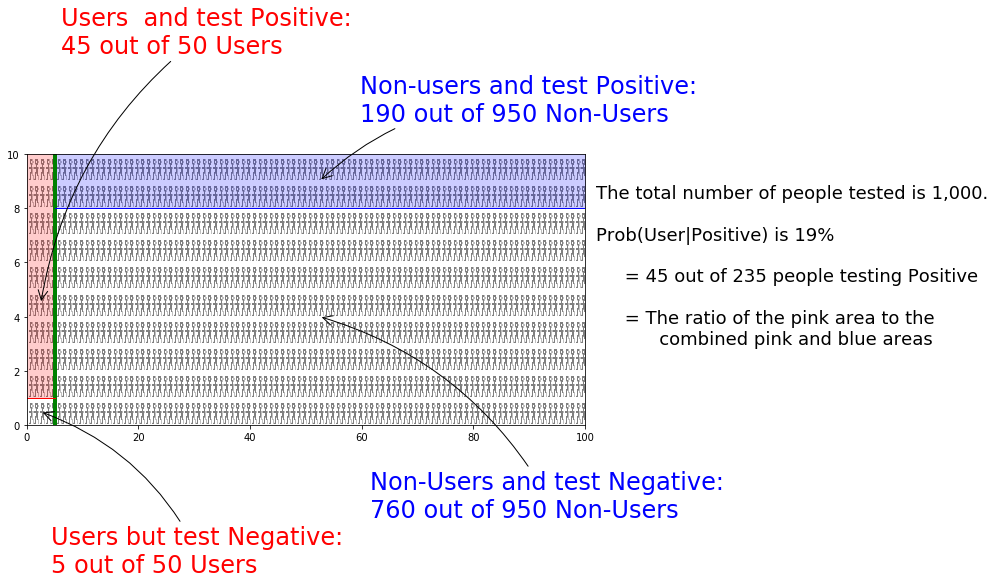
Drug testing: $P(user|positive) = \frac{P(user)·P(positive|user)}{P(user)·P(positive|user) + P(¬user)·P(positive|¬user)} $
Kul og nyttig setning, som likevel er litt i utkanten av det vi holder på med

QED Setning 11 i 7.7 s.808

\(P(A|C) = \frac{P(A)·P(C|A)}{P(A)·P(C|A) + P(¬A)·P(C|¬A)}\)

Aspekter / Filosofi#

Rekkefølgesymmetri mellom hendelsene#

Vi har ofte snakket som om en av hendelsene (betingelsen) kommer “før” den andre; det første terningkastet kommer før det andre, og lyst hår kommer før hvite sko. Det er lett for mennesker (særlig elever) å tenke sånn.

Matematisk er det derimot symmetri mellom hendelsene; det er ingen krav om at noe kommer først. Vi kan godt bytte rekkefølge på hendelsene.

Pedagogisk er det vel greit å holde seg til en rekkefølge i begynnelsen, uten at jeg har forskningsreferanser på dette.

Avhengighet er noe annet enn årsak!#

At to hendelser er avhengige trenger ikke å bety at noen årsak er involvert. I en populasjon kan andelen hvite sko blant de lyshårede være høy helt tilfeldig.

Det kan også være felles årsak til de to parametrene: Det viser seg at drukningsulykker på stranda ofte opptrer på dager med høyt salg av iskrem; det betyr ikke at iskrem er årsak til drukning.

Hvordan formidle#

Talltyper#