Én kontinuerlig parameter#
Forutsetninger og læringsmål#
Vi forutsetter eksemplene, begrepene og representasjoner fra TODO.
Vi vil foreløpig bare forholde oss til eksperiment hvor hvert utfall har bare én parameter. Vi måler altså én ting ved hert objekt/eksperiment.
Nå er parameteren kontinuerlig (f.eks. høyde). Det vil si at vi kan ordne og summere variabelen. Dermed kan vi for eksempel ta gjennomsnitt.
Referanser#
{{ref(“101 grep for å undervise i matematikk”, “26s210”)}}: Sannsynlighet og spill intro
Læreplan #
{{kompetansemål(“7”, “utforske og bruke hensiktsmessige sentralmål i egne og andres statistiske undersøkelser”)}} Merk “hensiktsmessige”
{{kompetansemål(“9”, “finne og diskutere sentralmål og spredningsmål i reelle datasett”)}}
Annet#
{{referanse(“qed 5-10 bind 1”, “6s s687 Beskrivende statistikk”)}}
{{referanse(“qed 5-10 bind 1”, “7s s727 Sannsynlighet”)}}
{{referanse(“Pind (2011)”, “?”)}}
Introduksjon#
Eksempler#

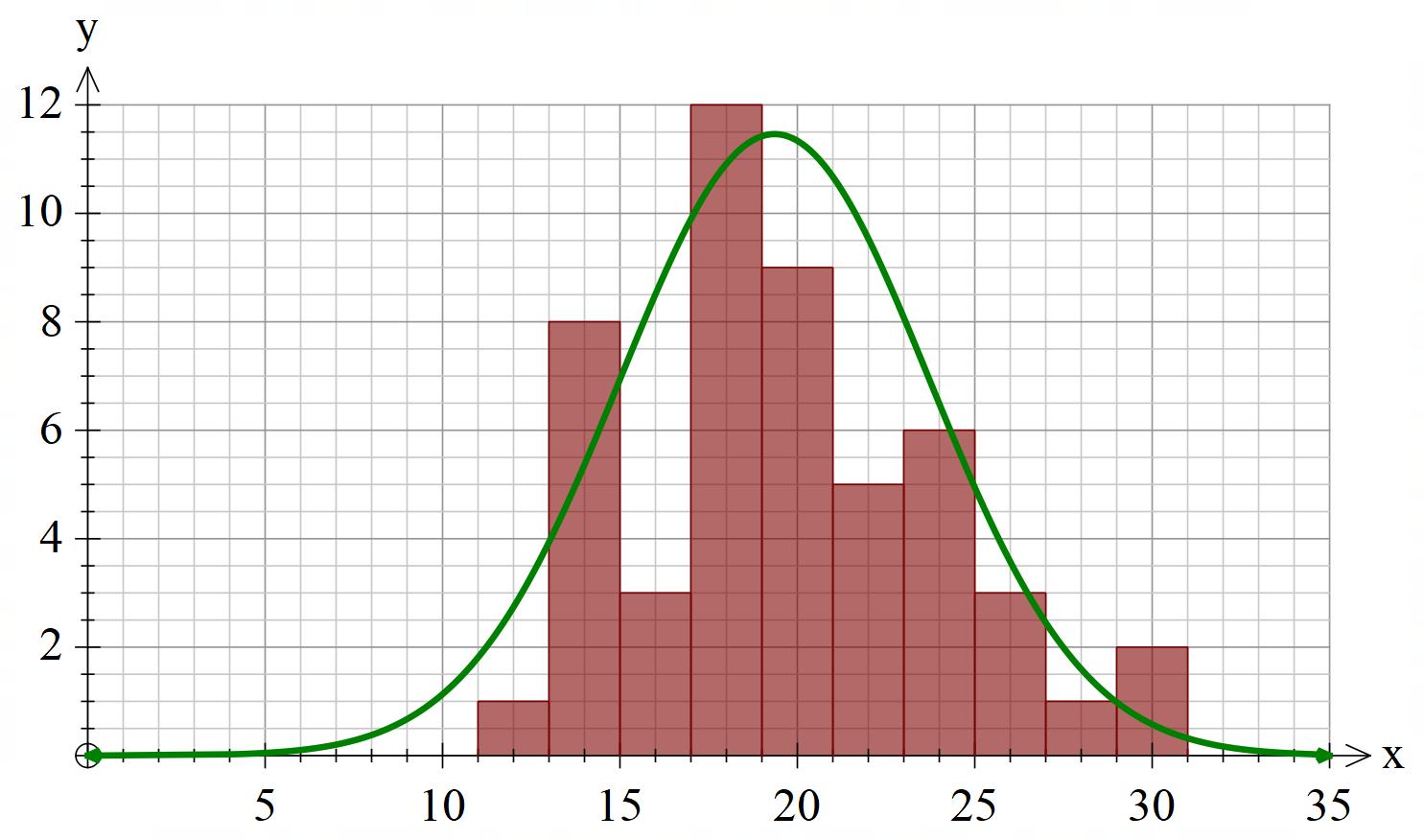
En tilfeldig populasjon hadde 27 objekter. Vi målte parameteren flyvetid. Fordelingen av flyvetider (gruppert i hele) er vist i figuren; maksimal flyvetid er 15.
Gjennomsnittlig flyvetid er 8.93; median flyvetid er 9.435. Første kvartil er 7.6 og tredje er 11.6; kvartilbredden er altså 4.0. Typetallene er 10 og 11.
Representasjoner#
Tabell#
På tall-linje#
Frekvensdiagram#
Vist over, under eksempel
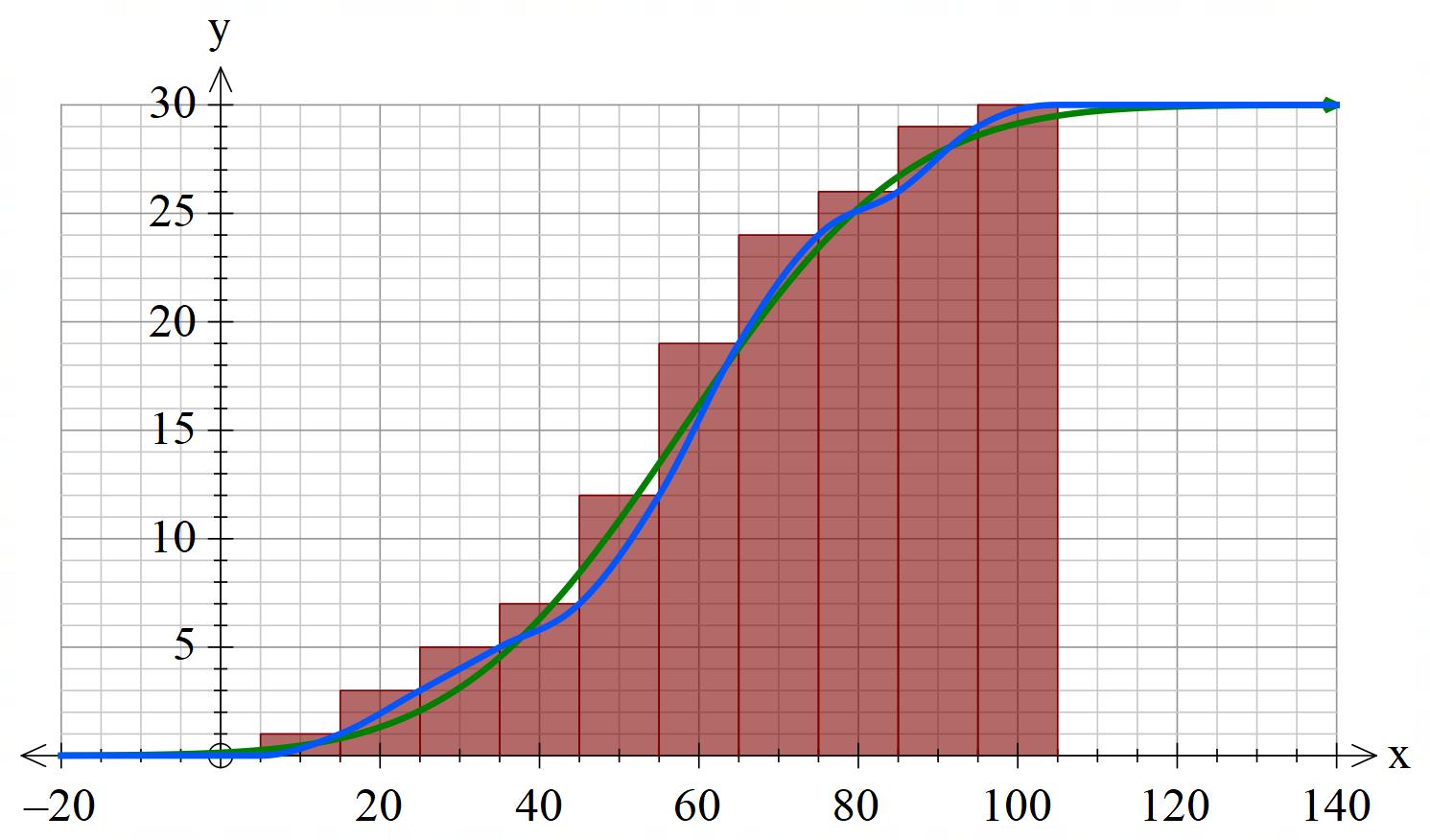
Kumulativt diagram#

Ikke så vanlig i skolen, men nyttig ellers.
Samme horisontale akse som frekvensdiagram. Men vertikal akse er nå hvor mange observasjoner som er mindre enn eller lik denne.
Excel#
Det viktigste herfra er at det finnes funksjoner for slike ting. Dere må kunne finne dem. Se gjerne over liste av funksjoner.
=Average, =Median, =mode.mult
Se også QED 6.2 “Diagram i regneark”
GeoGebra#
Mean, Median, Mode https://wiki.geogebra.org/en/Statistics_Commands
Begrep#
Fordeling#
Fordeling#
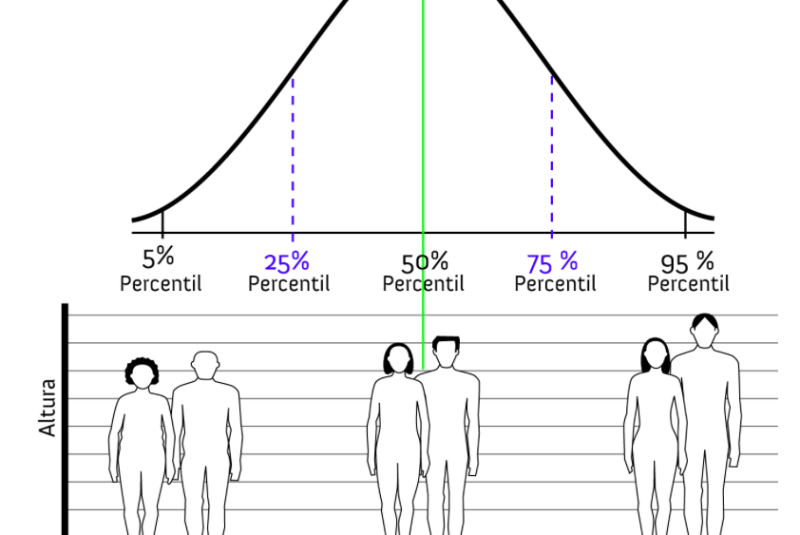
Normalfordeling#
Sentralmål#
Illustrasjon: https://www.geogebra.org/m/qd7tr6Pr
Se QED 6.2 Sentralmål s703
Gjennomsnitt#
Summen av alle delt på antallet.
Median#
Den midterste observasjonen
Typetall#
Typetall blir av noen regnet som et sentralmål, selv om typetallet ikke trenger å være sentralt.
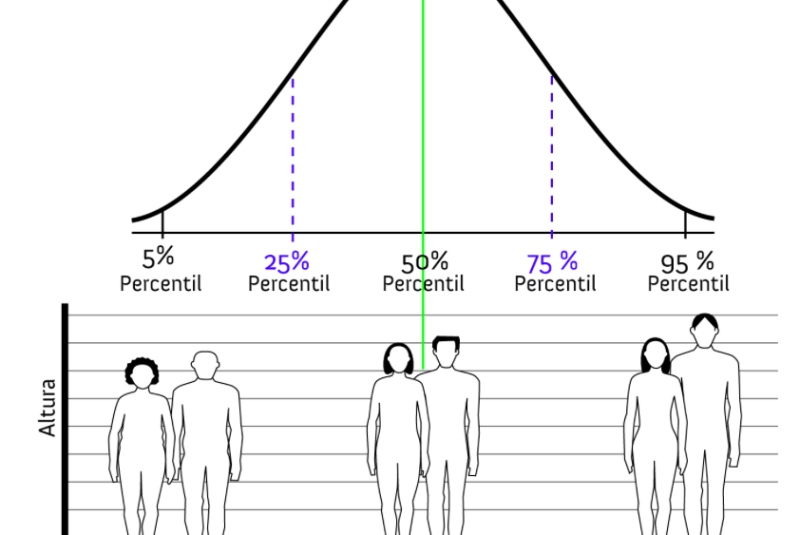
Prosentil (persentil)#

Vi får n-prosentilen av en rekke ved å sortere rekka; så ser vi på stedet som er n prosent bortover på lista. Vi får da at n% av rekka er ≤ n-prosentilen, mens resten av rekka er større. Denne definisjonen må justeres litt for å være nøyaktig når rekka har flere like tall.
25-prosentilen kalles 1. kvartil; 75-persentilen 3. kvartil. 50-persentilen er det samme som median.
Eksempel: I følge vekststudien i Bergen har norske tiårige jenter en 25-persentil-høyde på 136.5 cm. Det betyr at 75% av norske tiårige jenter er høyere enn dette. Se gjerne på den flotte figuren.
