2.3.7. Utfallsrom#
Introduksjon#
Utfallsrommet er mengden av mulige utfall. I matematikken betyr rom og mengde det samme. Siden vi snakker om mengder kommer vi fort bort i mengdelære; for eksempel bruker vi representasjoner for mengdelære som f.eks. Venn-diagram.
Siden den grunnleggende formelen i statistikk er at sannsynligheten for A er lik \(\frac{\textrm{størrelsen på rommet hvor } A \textrm{ er sann}}{\textrm{størrelsen på utfallsrommet}}\) er vi ofte interessert i størrelsen av utfallsrommet. Da må vi ofte inn i statistikk og kombinatorikk.
Et utfallsrom er uniformt om alle utfallene har like stor sannsynlighet. Det gjelder de fleste utfallsmengdene vi skal snakke om foreløpig.
Eksempel: Mynt og kron#
Utfallsmengden til myntkast er { {{tasklet.includes(“mynt”, hint=”m???”)}}, {{tasklet.includes(“kron”)}} }.
Det er {{tasklet.select(“sant”, [“?”, “sant”, “ikke sant”])}} at terningkast har et uniformt utfallsrom. Det er {{tasklet.select(“sant”, [“?”, “sant”, “ikke sant”])}} at myntkast har et uniformt utfallsrom.
Eksempel: Ett terningkast#
For eksempel er utfallsrommet av et terningkast mengden {⚀, ⚁, ⚂, ⚃, ⚄, ⚅}.
Eksempel: To terningkast#
Det er ikke alltid gitt hva som er ulike utfall. Hva om vi kaster to terninger?
Vi kunne tenke at hver mulig sum er et et utfall. Utfallsrommet er da 2,3,4,…,10,11,12. Det er mulig å se det sånn; men vi skal senere se at dette utfallsrommet er ikke uniformt!
Vi kan si at ⚀⚁ og ⚁⚀ er to ulike utfall. Vi sier altså at rekkefølgen betyr noe (ordnet utvalg). Da får vi (som vi senere skal se) et uniformt utfallsrom. Men det er bare ett av utfallene som gir summen 2, nemlig ⚀⚀. Derimot er det 6 av utfallene som gir summen 7: ⚀⚅, ⚁⚄, ⚂⚃, ⚃⚂, ⚄⚁ og ⚅⚀. Vi kan si at hendelsen “summen er 7” inntreffer ved seks ulike utfall. Det er mer praktisk og mye mer vanlig å se det på denne måten.
Representasjoner#
Vi er nå på grensen til statistikk. Mange av representasjonene hører først og fremst hjemme der, men jeg gjentar dem her.
Liste / tabell#
Venndiagram#
Utfallstre (valgtre) #
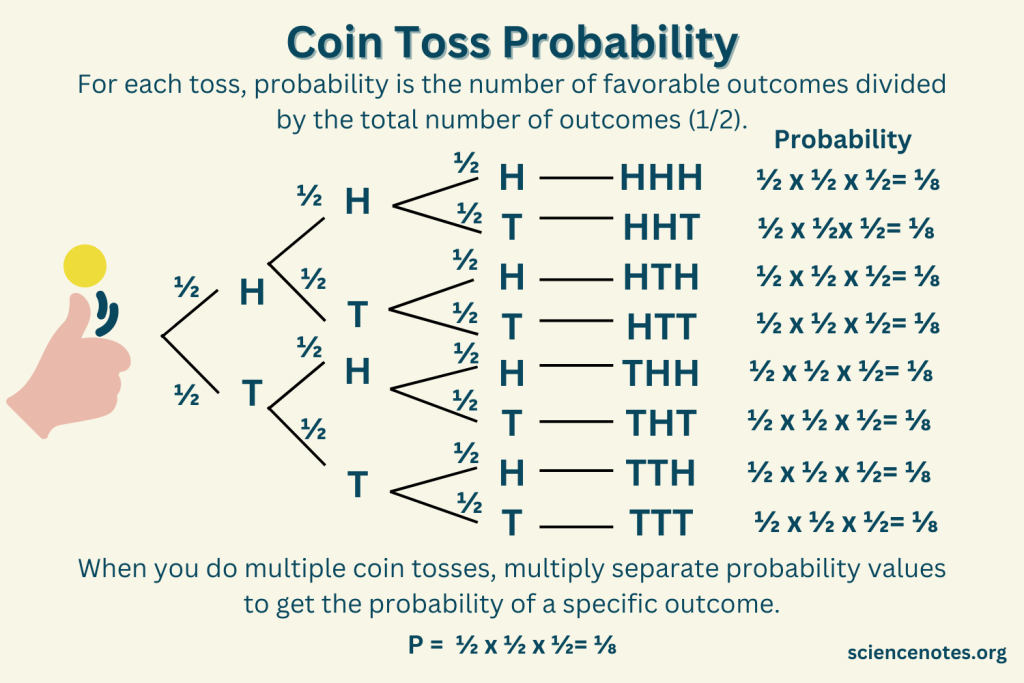
Dette er en representasjon av utfallsrommet.
Dette kalles også valgtre.
Algoritmer#
Lage en representasjon for et utfallsrom#
F.eks.
Liste (f.eks. når man har en parameter)
valgtre i kombinatorikk
Venn-diagram
Krysstabell (f.eks. når man har to terningkast)
