Overlappende hendelser#
Forutsetninger og læringsmål#
Vi skal nå snakke om at hendelser overlapper hverandre. Det betyr at de har felles utfall.
Introduksjon#
Eksempler#
Representasjoner#
Venn-diagram#
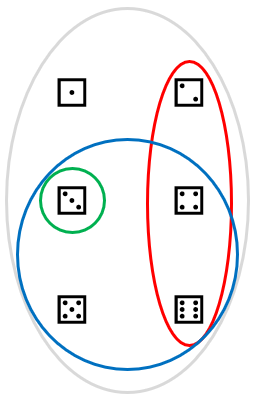
Kan det hende vi får både minst tre på en terning og samtidig to? Nei, det finnes ikke utfall hvor både hendelsen “minst tre” og “to” er sanne. De to hendelsene overlapper ikke. Snittet av deres utfallsrom er tomt.
Et utfallsrom kan representeres som et Venn-diagram der hvert utfall er et punkt og hver hendelse er en mengde. Et eksempel er vist i figuren. Utfallsrommet er avmerket med grått, hendelsen “partall” i rødt, hendelsen “minst tre” i blått og “tre” i grønt.
Kryssdiagram#
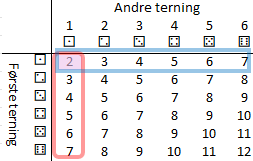
Når vi kaster to terninger: Finnes det eksempler hvor både den første terningen er ⚀ og den andre er ⚀? Ja, det finnes en hendelse hvor dette er sant: ⚀⚀.
I figuren til høyre er hendelsen hvor første terning er ⚀ markert med blått og hendelsen hvor andre terning er ⚀ markert med rødt. Rommet av det (ene) gunstige utfallet ⚀⚀ har lilla bakgrunn.
Digitale verkøty#
Algoritmer#
Lover#
Addisjonssetningen: Eller#
For ikke-overlappende hendelser#
Når to hendelser A og B ikke overlapper kan vi legge deres utfallsrom ved siden av hverandre: Sannsynligheten for at A eller B er sann er lik sannsynligheten for A + sannsynligheten for B. \(P(A∨B) = P(A) + P(B)\).
For overlappende hendelser: Fellesområdet må ikke telles to ganger!#
Hva er sjansen for å få ⚀ på minst én av terningene? Hva er altså sjansen for å få ⚀ på den første terningen eller å få ⚀ på den andre (eller begge)?
Sjansen for å få ⚀ er \(\frac{1}{6}\), dvs. \(\frac{6}{36}\) på hver av terningene. Men vi kan ikke addere dette og få \(\frac{2}{6}\); det blir for mye. (Tenk om noen ville addere “sjansen for å få minst tre på første terning” og “sjansen for å få minst tre på andre terning” på denne måten: Det ville bli \(2·\frac{4}{6} → \frac{4}{3}\) som er >1!)
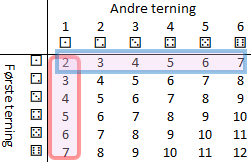
Riktig addisjonslov#
Hendelsen “⚀ på første terning” og “⚀ på andre terning” overlapper. Sjansen for hver av dem er en av trettiseks: \(P(⚀⚀) = \frac{1}{36}\).
Formelen blir riktig om vi trekker fra det det vi har telt to ganger: Sjansen for at A eller B er sann er lik sjansen for A pluss sjansen for B minus sjansen for begge. \(P(A ∨ B) = P(A) + P(B) - P(A∧ B)\). I figuren er
\(P(A)\) det røde området,
\(P(B)\) det blå,
\(P(A ∨ B)\) (A eller B) er kombinasjonen (sjansen for at minst en av dem er sann) altså union, ∪
\(P(A ∧ B)\) (A og B) er overlappet (sjansen for at begge er sanne) altså snitt, ∩
A og B kan være hendelser med mer enn ett utfall. Sjansen for å få ⚂, ⚃, ⚄ eller ⚅ på begge terningene = \(\frac{4}{6} + \frac{4}{6} - \frac{16}{36} → \frac{8}{9}\). Sjansene \(\frac{4}{6}\) og \(\frac{16}{36}\) kan vi finne ved å telle i krysstabellen.
Addisjon (+), eller (∨), union (∪) og “minst én” har med hverandre å gjøre.
For én terning: <span=example>Hva er sjansen for å få både minst tre og partall? Dette er lik sjansen for å få minst tre (\(\frac{4}{6}\)) pluss sjansen for å få partall (\(\frac{3}{6}\)) minus sjansen for overlappet (\(\frac{2}{6}\)). Svaret blir \(\frac{5}{6}\), som stemmer om vi teller opp i Venn-diagrammet.
Hvordan formidle#
Addisjonssetningen: Eller#
Repetisjon (?): Addisjon for ikke-overlappende hendelser#
Når vi har én parameter kan vi addere sannsynligheter: Sannsynlighet for å få ⚁ eller ⚂ er lik sannsynligheten for ⚁ + sannsynligheten for ⚂. Dette kan vi tegne opp på en tall-linje. En annen representasjon er bare å tegne opp utfallsrommet: ⚀⚁⚂⚃⚄⚅.
Dette gjelder generelt så lenge to hendelser ikke overlapper: Sannsynligheten for at A eller B er sann er lik sannsynligheten for A + sannsynligheten for B. \(P(A∨B) = P(A) + P(B)\).
Misforståelse#
Hva er sjansen for å få ⚀ på minst én av terningene? Hva er altså sjansen for å få ⚀ på den første terningen eller å få ⚀ på den andre (eller begge)?
Sjansen for å få ⚀ er \(\frac{1}{6}\), dvs. \(\frac{6}{36}\) på hver av terningene. Men vi kan ikke addere dette og få \(\frac{2}{6}\); det blir for mye. (Tenk om noen ville addere “sjansen for å få minst tre på første terning” og “sjansen for å få minst tre på andre terning” på denne måten: Det ville bli \(2·\frac{4}{6} → \frac{4}{3}\) som er >1!)

Riktig addisjonslov#
Hendelsen “⚀ på første terning” og “⚀ på andre terning” overlapper. Sjansen for hver av dem er en av trettiseks: \(P(⚀⚀) = \frac{1}{36}\).
Formelen blir riktig om vi trekker fra det det vi har telt to ganger: Sjansen for at A eller B er sann er lik sjansen for A pluss sjansen for B minus sjansen for begge. \(P(A ∨ B) = P(A) + P(B) - P(A∧ B)\). I figuren er
\(P(A)\) det røde området,
\(P(B)\) det blå,
\(P(A ∨ B)\) (A eller B) er kombinasjonen (sjansen for at minst en av dem er sann) altså union, ∪
\(P(A ∧ B)\) (A og B) er overlappet (sjansen for at begge er sanne) altså snitt, ∩
A og B kan være hendelser med mer enn ett utfall. Sjansen for å få ⚂, ⚃, ⚄ eller ⚅ på begge terningene = \(\frac{4}{6} + \frac{4}{6} - \frac{16}{36} → \frac{8}{9}\). Sjansene \(\frac{4}{6}\) og \(\frac{16}{36}\) kan vi finne ved å telle i krysstabellen.
Addisjon (+), eller (∨), union (∪) og “minst én” har med hverandre å gjøre.
