Funksjoner#
Funksjoner blir f.t. undervist av Johannes Kleppe i MA102, og blir derfor ikke tatt seriøst her. Det eksisterer likevel noen eksperimenter.
Introduksjon#
En funksjon er noe som tar noe (f.eks. et tall) inn og leverer noe ut. Introduseres vel best ved representasjoner og eksempler.
Det kreves for en funksjon at hver verdi inn gir én verdi ut. Men flere verdier inn kan godt gi samme verdi ut.
Eksempler fra nettet. Google Trends? Coronasmite? ssb? TODO
Representasjoner#
Mye av det følgende er generelt om funksjoner. Det er muligens enklere å forstå om man har lest om eksempel-funksjonstyper først.
Ord#
Mange av funksjonene vi snakker om i skolen kan defineres, f.eks. kan \(f\) defineres som funksjonen med \(x\) som argument som gir verdien \(x^2 + 2\).
Variable som har funksjoner som verdi kalles ofte \(f\) (som i eksempelet over), \(g\) etc.
Det som kommer inn kalles ofte parameter. Det er \(x\) i eksempelet. Parameteren er en variabel som kan brukes i funksjonsdefinisjonen. Når en funksjon appliseres (brukes) får parametrene verdier f.eks. om vi sier \(f(3)\) får \(x\) verdien \(3\) i dette tilfellet og funksjonen kan regnes ut i følge definisjonen så vi får \(3^2 + 2\) som blir \(11\). Vi kan si at \(f(3) → 11\). Vi sier da at 2 blir argument til funksjonen. Mange blander begrepene parameter og argument. Mengden av alle lovlige argument-verdier er definisjonsmengden.
De fleste funksjoner vi snakker om i skolen har bare én parameter.
Det som går ut kalles ofte returverdi (særlig av programmerere?) eller funksjonsverdi, eller bare verdi. Mengden av alle mulige returverdier kalles verdimengden.
Engelsk#
Funksjon = function; definisjonsmengde = domain; verdimengde = range (ordet ‘codomain’ betyr nesen det samme).
Formelspråk#
Tradisjonelt formelspråk: Krøkkete?#
I tradisjonelt formelspråk sier vi f.eks. at \(f(x) = 2x + 3\). Vi sier altså funksjonsnavnet/-variabelen, parentes med argument, et likhetstegn og så funksjonsdefinisjonen.
Man kan mene at dette er en krøkkete notasjon:
man kan ikke notere en funksjon uten å ha et navn på den.
man tilslører at f egentlig er en variabel som peker på en funksjon, på samme måte som n (typisk) peker på et tall og A på en påstand.
parentesen har en helt annen funksjon enn det parenteser vanligvis har. Hvorfor skal vi ha parentes her?
notasjoner for deriverte blir kunstige.
\(f\) er egentlig en variabel (som peker på en funksjon), og skal i kursiv.
Lambda-syntaks#
En mer naturlig syntaks er muligens lambda-syntaks (oppkalt etter den greske bokstaven λ). Syntaksen er et λ-tegn, så argumentene, så et punktum og så definisjonen. Et eksempel er \(f = λ x . 2x + 3\). Dette skal leses “f er lik funksjonen som har x som argument og har verdien 2x + 3. Denne er dessverre ikke vanlig i skolen.
Nøkkelordet lambda finnes i Python og andre funksjonelle programmeringsspråk.
Man kan argumentere for at lambdasyntaks er enklere for elever som ikke er vant til den vanlige. Lambdasyntaks er også mer matematisk robust og enklere å utvide.
Et liknende symbol er ↦ (maplet).
Funksjonsuttrykk og bokstavuttrykk#
Er det forskjell på funksjonen \(2x + 3\) og bokstavuttrykket \(2x + 3\)?
De to er svært like; de fleste elever trenger ikke bekymre seg om forskjellen. Det følgende er mest relevant for nerder og lærere:
Vi kan likevel si det er en forskjell på funksjonen og bokstavuttrykket: I den første er det underforstått at \(x\) er en parameter. x er altså noe som “bor i” funksjonen. Det er dette vi uttrykker ved å si “\(f(x)\)” eller “\(λ x .\)”. Funksjonen \(f(x) = 2x + 3\) er nøyaktig den samme funksjonen som \(f(y) = 2y + 3\), og de er helt uavhengig av hva \(x\) og \(y\) er utenfor funksjonen. Bokstavuttrykket \(2x + 3\) er derimot avhengig av verdien av \(x\). I Python har man det samme: Linja def f(x): lager en egen x inni funksjonen.
Et annet eksempel er funksjonen \(f(x) = 2x + 3y\). Denne funksjonen er avhengig av hva verdien av \(y\) ellers er, men uavhengig av \(x\). Vi har for eksempel at \(f(3)\) er \(2·3 + 3y\). Funksjonen er en helt annen enn \(g(y) = 2x + 3y\); Vi har at \(g(3)\) er \(2x + 3*3\).
Maskin som får noe inn og gir noe ut#
En funksjon kan betraktes som en maskin som tar noe (parameter) inn og gir noe (returverdi) ut. Dette får fram at en funksjon også kan betraktes som en handling (f.eks. “opphøy argumentet i andre og legg til to”)

Fig. 55 Oppskrift på grove brød#
En liknende metafor er “oppskrift”.
Tabell#
En funksjon kan representeres ved en tabell. Hver linje blir et mulig argument. Om definisjonsmengden er uendelig stor (som den vanligvis er, f.eks. om den er lik ℝ) har tabellen uendelig mange linjer. Det er en kolonne for argumentet og en for returverdien.
Det er krav om at hvert argument bare gir én returverdi. Altså kan hver verdi bare forekomme i én linje i venstre kolonne; men samme verdi kan gjerne forekomme flere ganger i høyre kolonne.
Teknologi: Regneark#
I regneark kan mange tabeller regnes som funksjoner; riktignok kan de ikke være uendelig lange.
For eksempel kan funksjonen som tar \(x\) som argument og har verdien \(x^2 + 3\) representeres ved at venstre kolonne har mange argument-verdier (altså inn-verdier) (kanskje cellen A3 formelen =A2 + 0.1), og høyre kolonne tilsvarende funksjonsverdier (kanskje B3 har formelen A3^2 + 3).
Noen vil også mene at en regneark-formel modellerer det samme som en funksjon.
Grafer, kurver#
Dette forutsetter kjennskap til koordinatsystem.
Kurver er så viktig representasjon på funksjoner i skolekulturen at kurve-representasjonen nesten blir forvekslet med selve funksjonsbegrepet.
Merk at ordet graf brukes i andre betydninger, f.eks. et nett av noder og kanter. Et Google-søk på graf gir et inntrykk. Vi vil derfor foretrekke ordet kurve.
Vi kan plotte definisjonsmengden på vannrett akse og verdimengden i loddrett. For hver mulige argument (hvert punkt i definisjonsmengden) (3 i eksempelet under) regner vi ut funksjonsverdien (5 i eksempelet under) og tegner en prikk på punktet (argumentverdi, returverdi) (i eksempelet under er punket (3,5) merket med rød flekk). Gjør vi dette for mange punkter får vi en graf:
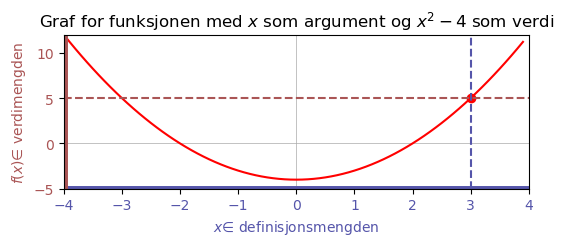
Det er altså et krav om at enhver argument gir én bestemt returverdi. En graf for en funksjon kan altså ikke ha to punkter “over hverandre”. Derimot er det lov at to argument gir samme returverdi: En graf kan ha to punkt “ved siden av” hverandre.
GeoGebra#
GeoGebra er egnet til å tegne grafer, også interaktive. Man kan for eksempel skrive funksjonen f(x) = x^2 - 3.
Tips til læring#
NDLA koordinatsystem og NDLA tallmengder. [Klaveness et al., 2019] 29 s216 Å skissere grafer og 30s218.
Fred og frank er to treningsfanatikere som løper fra A til B. Fred løper halvparten av veien og går resten. Frank løper halvparten av tiden og går resten. De går og løper like fort som hverandre. Hvem kommer først? [Mason et al., 2010] “Fred and Frank, p.155”
Man kan også bruke GeoGebra til å illustrere at en kurve består av mange punkt. Dra i a-slideren under:
Doble tall-linjer#
Doble tall-linjer er en mye mer uvanlig representasjon, men se [Klaveness et al., 2019] 82 s322.
Her ligger verdimengden og definisjonsmengden ikke i kryss, men parallelt. Det som i kurve-representasjon er et punkt er i doble tall-linje-representasjonen en linje mellom et punkt i verdimengden og tilsvarende i definisjonsmengden:
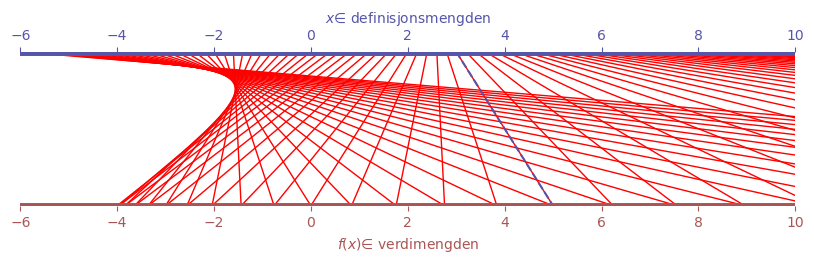
vi ser flere ting. Hva betyr følgende, og hva tilsvarer det i en graf?
Definisjonsmengden har én strek fra hvert punkt.
Verdimengden har ingen streker til verdier <4.
Hvert punkt >−4 på verdimengden har strek fra to punkt på definisjonsmengden.
Er vi >0 på definisjonsmengden ser det ut til at strekene “sprer seg”. Er vi <0 ser det ut til at strekene “samler seg”. Hint: Derivert
Dette er en nyttig representasjon
fordi den uttrykker bedre visse egenskaper, f.eks. at funksjoner kan kobles i serie
fordi den hjelper oss til å forstå at det er vanskelig å lese en representasjon første gang. For elever er “vanlig” koordinatsystem like vanskelig som dobbel tall-linje.
Python#
Vi kan også bruke ordet lambda, men det er dessverre ikke så vanlig i skolen.
def minFunksjon(x):
return (x * 2) + 3
Definisjons- og verdimengde. Definisjonstype? Verditype?
Scratch#
I Scratch kan man lage sine egne klosser. Disse kan ta argumenter, men dessverre ikke returnere verdier. reporters?
Janviers tabell#
Claude Janvier påsto det fantes fire representasjonsformer for representasjon av funksjon:
Situasjon
Tabell
Graf
Funksjonsuttrykk.
Man kan sette opp en 4×4-matrise TODO. https://www.nkhansen.com/tag/janviers-tabell/
Overgangene:
Som det vil framgå av dette dokumentet mener Ellef vi kan finne flere representasjonsspråk.
Småstein og fliser#
Algoritmer#
Mye av det følgende er generelt om funksjoner. Det er muligens enklere å forstå om man har lest om eksempel-funksjonstyper først.
Finne verdi#
Dette er på en måte den grunnleggende algoritmen med funksjoner: Gå fra et punkt i definisjonsmengden til en i verdimengden. Dette kalles også å applisere funksjonen, selv om dette ordet ikke er så vanlig i norsk skole.
Regne ut verdi#
Om vi har et funksjonsuttrykk for funksjonen: Vi setter inn et argument (f.eks. 3) inn for parameteren (f.eks. x) i funksjonsuttrykket. Er funksjonsuttrykket for eksempel \(x^2 - 3\) får vi da \(3^2 - 3\)..
Lese av graf#
En annen måte å finne en verdi på er å lese av en graf. Man finner linja hvor x er for eksempel 3, og finner stedet hvor grafen treffer denne linja.
Aspekter#
Funksjon som oppskrift#
Når man lærer om funksjoner er det vanlig å tenke på funksjon som en oppskrift. Noen av representasjonene legger også opp til det.
Funksjon som en mengde par#
Senere vil noen studenter tenke på funksjon som en (uendelig) mengde par (Bourbaki). Dette er en definisjon som er matematisk mer robust, og en forståelse som er vanlig blant matematikere.
“Å gjøre” → “å være”#
Det kan altså skje en overgang fra å se på funksjon som noe man gjør til noe som er. En slik overgang kan skje på mange steder i matematikken (Sfard, 1991). Den er didaktisk svært interessant TODO
Talltyper#
Vi har tidligere snakket om talltyper som ℕ (Naturlige tall) og ℝ (Relle tall).
En funksjon (f.eks. \(f = λx . x^2 + x\)) kan for eksempel ha et argument av typen ℝ og returnere et resultat av typen ℝ. Da kan vi snakke om at \(f\) er av typen ℝ → ℝ.
En funksjon avrund vil bare returnere heltall; Den vil altså ha typen ℝ → ℤ.
En funksjon adder, definert ved \(adder = λ addend1, addend2 . addend1 + addend2\) tar altså to argument og legger dem sammen. Den vil ha typen ℝ × ℝ → ℝ.
Læring#
Gjøres ofte med eksempler; jeg argumenterer for at “virkelige”, kompliserte eksempler er bedre enn “enkle” eksempler som første- og andregrad.