Minus#
Forutsetninger og læringsmål#
Vi skal introdusere subtraksjon (minus) og hvordan det kan representeres i tellbar mengde-språket. Vi skal introdusere to tankemodeller for subtraksjon: forskjell og fjerne. Vi skal også introdusere en ny talltype (negative tall).
Du skal kunne
Subtrahere ved forskjellige algoritmer
Representere både forskjell-subtraksjon og fjerne-subtraksjon med både småstein og på tall-linja
Modellere praktiske eksempler som forskjell- eller fjernesubtraksjon
Læreplanen TODO#
Annet#
[Hinna et al., 2016] 1.4.2 Subtraksjon s75
[Pind, 2011] Subtraksjon s101
Introduksjon#
Olav har seks sjokolader, mens Håkon har bare fire. Hvor mange flere har Olav? Dette er eksempel på forskjell eller differanse. Vi skal si at forskjellen på 3 og 5 er −2 (ikke at forskjellen er 2). Den tilhørende handlingen er å sammenlikne.
Anne har seks sjokolader, mens Helene spiser fire av dem. Hvor mange har Anne igjen? Dette er eksempel på å fjerne, trekke fra eller ta bort. Den tilhørende handlingen er å ta bort.
Ordforklaring: Subtrahere
Det latinske ordet sub-traksjon betyr omtrent det samme som å trekke fra eller ta bort.
Representasjoner#
Småstein#
Forskjellen på for eksempel 
og 
er 
. Vi kan sette dem opp under hverandre:
(Vi bruker fortsatt bakgrunnsfargen 
bak svaret og stiplet linje mellom overgangene).
Fargene på og er ikke nødvendige, men vi bruker dem for ekstra tydelighet.
Her begynner både subtrahend og minuend til venstre, og differansen (svaret) er mot høyre.
(TODO: Her forutsetter jeg på en måte at vi går fra høyre; er det ok?)
Et opplegg om «subtraction as difference finnes på NCETM: [Lærerveiledning],(https://www.ncetm.org.uk/media/yshp1gxs/ncetm_mm_sp1_y2_se12_teach.pdf) nedlastbar .pptx og film
Fjerne-subtraksjon er altså at vi har og skal fjerne . Dette kan vi også sette opp under hverandre:
Her er minuend fra høyre, og differansen er mot venstre.
Sammenlikne de to oppsettene. Selv om de begge representerer 5−3, og har samme svar, er de litt forskjellige.
78 − 2 er . Tenkte du forskjell forskjell-subtraksjon eller fjerne-subtraksjon her? Hva er lettest?
78 − 75 er . Tenkte du forskjell forskjell-subtraksjon eller fjerne-subtraksjon her? Hva er lettest?
Ord#
Differanse er resultatet av en subtraksjon. For eksempel er differansen mellom 2 og −5 lik . Vi bruker også ordet minus, men å “minusere” brukes ikke.
Du husker kanskje at to ting som adderes kalles addender. De to tingene som subtraheres kalles minuend og subtrahend. Vi har altså at addend + addend blir sum og at minuend - subtrahend blir differanse. I eksempelet 5 − 2 er altså 5 , 2 er og 3 er .
Formelspråk#
Symbolet for minus er −. Minus-streken er (i god typografi) en annen strek enn bindestrek -, intervallstrek ‒ og tankestrek —, men når vi skal skrive kjapt er det noen enklere å bruke den bindestreken som finnes på tastaturet (- i stedet for −). I oppgaver i dette dokumentet kan (og må) du skrive subtraksjon (og, senere: negative tall) med bindestrek: −2 skal skrives
Minussymbolet skrives vanligvis infiks ( minuenden og subtrahenden): 5 − 2.
Vi kan også blande småstein og formelsumbol: 
- 
blir 
.
Skrivemåten \(a - b - c\) skal leses \((a - b) - c\). Dette er et valg samfunnet har tatt for formelspråket; vi kunne valgt annerledes. Valget gjelder i utgangspunktet bare formelspråket, ikke andre representasjoner. Valget handler i utgangspunktet ikke om matematikk (eller regnerekkefølge); det handler om hvordan representasjoner i formelspråket skal tolkes. En del lærere bruker dessverre ordet “regnerekkefølge” om slikt; dette kan forvirre elevene til å tro at valget berører noen egenskap ved matematikken.
10 − 4 − 1 er altså lik .
Tall-linje#
https://phet.colorado.edu/en/simulations/number-line-operations
https://phet.colorado.edu/en/simulations/number-line-distance
Cambridge espresso “The number line” og tilsvarende på norsk
Introduksjon#
Vi har representert tall med firkanter, f.eks. . Noen ganger er det praktisk å legge til en strek til venstre, “der vi skal begynne å telle”:
|. Vi assosierer “positiv retning” mot høyre. Dette har vi egentlig gjort også ovenfor.
Vi skal nå introdusere tall-linje-representasjonsspråket. Dette er en linje som peker mot høyre. Et punkt er 0, og mer positive tall ligger lengre til høyre. 5 representeres som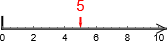 
, altså et sted på linja. 5 kan også representeres som 
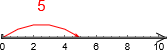, altså som bevegelsen fra 0 til punktet.
Linja er i prinsippet uendelig lang. Derfor tegner vi bare en pil mot høyre for å vise at den fortsetter. Vi kunne ha tegnet lengre: 
. Det hender også vi tar med et utsnitt uten 0. Tallet 99 kan for eksempel representeres som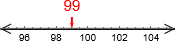 
Det er alltid fint å forbinde læring med noe elever kan fra før. Tall-linjer kan assosieres med avstander eller med termometre.
Addisjon på tall-linja#
Vi husker at 2 + 3 kan representeres som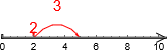 
. Vi begynner altså på første addend og tegner en pil med lengde andre addend. Pilretningen er mot høyre, fordi vår kulturs tall-linje går mot høyre. Vi kommer da til summen.
Forskjell-subtraksjon på tall-linja#
Skal vi representere forskjellen på
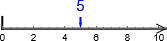og
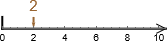, vil vi få fram hvor langt det er mellom dem:
.
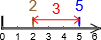Med andre ord: Vi finner svaret ved å begynne på 2, gå til 5 og telle opp hvor mange hopp vi har.
Vi kan sammenlikne med representasjonen vi hadde tidligere:
Som sagt kommer svaret her til høyre.
Fjerne-subtraksjon på tall-linja#
Vi fjerner fra høyre.
Om vi har
og går to mot venstre, vil svaret komme fram til venstre (det er egentlig derfor vi fjerner fra høyre):
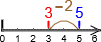som også kan tegnes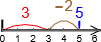 
Vi kan sammenlikne med representasjonen vi hadde tidligere:
Som sagt kommer svaret her til venstre.
Subtrahere som å snu#
Å subtrahere er altså å gå mot venstre, iallfall når vi subtraherer positive tall. Det er å gå motsatt vei av “vanlig vei” (som i vår kultur er mot høyre). Det er altså på en måte å snu.
Oppgaver om representasjoner av subtraksjon#
Tegn (på papir) stykket 7−3 som
Tellbar mengde, ved å ta bort (hvordan vil du tegne de som er “tatt bort”?)
Tellbar mengde, som forskjell (differanse)
Tall-linja, som to bevegelser (den første fra 0)
Tall-linja, som en bevegelse (fra 7)
Tall-linja, som differanse (forskjell) på 7 og 3
Algoritmer#
Jeg oppfordrer leseren til å prøve å finne ut av hvilken algoritme hen selv bruker; hva skjer i hodet ditt når du regner ut f.eks. 102 − 3 som blir ?
Dette bør nolk skrives mer av noen som vet hva som faktisk foregår.
Telle nedover#
Denne algoritmen fungerer både på en tall-linje og på tellbar mengde (f.eks. på fingrene). Den består i å starte i minuenden (f.eks. i 
, altså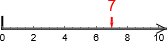 
og å gå mot venstre / trekke fra så mange som subtrahenden (f.eks. ta bort 3 
eller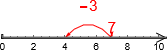 
. Det man står igjen med, altså der man er, blir differansen.
Denne algoritmen fungerer både på en tall-linje og på en tellbar mengde (f.eks. på fingrene). Den er egnet når minuenden er relativt liten. Subtrahenden kan godt være stor: Dette fungerer på f.eks. 107−3 .
En tall-linje fungerer også fint om man går forbi en “rund” grense (f.eks. 103−7). Har man tellbar mengde med 
ere, må man bruke noen spesialtriks (veksling, som vi kommer til nedenfor).
5 − 1 er .
9 − 2 er .
104 − 2 er .
102 − 3 er (ikke så vanskelig som man skulle tro om man har tall-linje i hodet?)
Legg merke til at selv om de to siste oppgavene ser like ut på overflaten, byr de på helt forskjellige vanskeligheter for eleven, og man bør tenke på forskjellig måte.
Ta bort likt fra minuend og subtrahend#
Om vi zoomer inn på detaljene er det kanskje følgende som foregår?
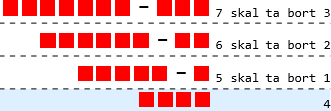Om vi tar vekk en 
er fra både minuenden og subtrahend blir differansen det samme. Vi kan faktisk ta bort også en er eller hva som helst annet, og differansen blir fortsatt det samme. Se på følgende utregning:
Dette er en god snarvei sammenliknet med å telle ned én og én.
Dette er også ofte en god måte å gjøre hoderegning på.
77 − 37 er (ta bort 7 fra minuend og subtrahend).
73 − 34 er (kanskje ta bort først 3, og så 30? I så fall kommer vi 40 − 1.
302 − 4 er (her er det mulig å være innom regnestykket 300 − 2).
302 − 107 er
427 − 316 er .
Kolonnealgoritme #
Du husker kanskje at for addisjon kunne man sortere ere og ere i egne kolonner, og man kunne også veksle:
.
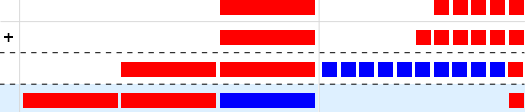Tilsvarende kan man også gjøre med subtraksjon. Her bruker vi en overgang på å trekke fra minuend og subtrahend, og så en til på å fjerne }:
De fleste vil gjøre begge samtidig. Det tilsvarer at vi subtraherer tierne for seg og enerne for seg:
58 − 12 er . Om du er fristet til å gjøre dette i hodet: Hvordan gjør du det? Hvordan kan du forklare en elev hva som foregår?
77 − 36 er .
78 − 37 er .
48 − 5 er .
Veksling (låning)#
Hva skjer om vi går tom for ere, for eksempel i 32 − 15? Da må vi veksle:
altså 
Vi avrunder dette med å vise et oppsett av samme regnestykke som følger algoritmen “ta bort likt fra minuend og subtrahend”. Her er altså hver overgang én linje:
54 − 36 er . Legg merke til hvordan du tenker, og ikke gå for fort fram. Om du gjør feil: Hva skyldes feilen?
En elev får oppgaven 54 − 36 og svarer 28. Hva kan eleven ha tenkt?
62 − 16 er . Om du er litt usikker på svaret: Hvordan kan du sjekke svaret? (hint: 16 + er 62).
52 − 7 er . Her vi noen tenke tall-linje, mens noen vil tenke veksling.
77 − 37 er .
Kommutativ lov#
Vi husker kanskje den kommutative lov for addisjon: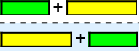 
, \(\overset{a + b}{\underset{b + a}{⇵}}\).
Norges befolkning + Sveriges befolkning Sveriges befolkning + Norges befolkning
Tilsvarende for subtraksjon. Det er ikke sånn at \(a - b\) er det samme som \(b - a\). Det kan vises med et eksempel, for eksempel 2 for \(a\) og 3 for \(b\). 3 − 2 er mens 2 − 3 er . Det er altså ikke noen kommutativ lov for subtraksjon.
Norges befolkning − Sveriges befolkning Sveriges befolkning − Norges befolkning.
En elev sier at 5 − 8 er 3. Hva kan eleven ha tenkt?
En elev sier at 45 − 38 er 13. Hva kan eleven ha tenkt? Denne er avansert, men ikke mer avansert enn det lærere kommer borti.
Assosiativ lov #
Den assosiative gjelder heller ikke: Det stemmer ikke generelt at \(\overset{a - (b - c)}{\underset{(a - b) - c}{↓}}\).
Formelspråket: − tolkes venstre-assosiativt#
Hva betyr det om noen skriver \(a - b - c\)? Vår kultur har valgt å la dette bety \((a - b) -c\). Vi sier at vår kultur lar subtraksjon i formelspråket være venstre-assosiativt. Dette tilsvarer at vi subtraherer forløpende i den rekkefølgen vi leser.
8 − 5 − 2 er .
10 − 6 − 5 er .
Dette er altså en egenskap ved formelspråket og ikke en egenskap ved selve matematikken.
a − a → 0#
Dette kan vi representere som 
. Om litt skal vi introdusere tallet 0 (
) for “ingen”.
Norges befolkning − Norges befolkning er .
a − −b → a + b#
TODO
Sammenheng med addisjon#
Vi har at om − blir , er + lik . Det ser vi tydelig i småsteinsrepresentasjon av forskjell-subtraksjon og fjerne-subtraksjon . Som regel kan vi skrive \(\overset{5 - 2 = 3}{\underset{3 + 2 = 5}{↓}}\) (om vi godtar et likhetstegn som vi strengt tatt ikke har definert ennå).
Dette er egentlig bare et eksempel: Men kanskje vi kan overbevise oss om at slik må det alltid være for alle tall? Da kan vi definere loven for variable: \(\overset{a - b = c}{\underset{b + c = a}{↓}}\).
Gitt at 100 − 2 = 98, klarer du da å regne ut 2 + 98? Det blir .
Norges befolkning minus 408 000 er 5 000 000. Norges befolkning er derfor (vi har egentlig ikke definert så store tall ennå).
Hva kan adderes og subtraheres? Om epler og kilogram#
Hva er det som kan adderes og subtraheres?
Mange vil svare tall. Så langt har vi sett på heltall, og senere skal vi se på desimaltall.
Men vi har også addert firkanter ⬛ og hjerter ❤️. I grunn kan vi addere det meste. Vi kan addere alt som kan telles. Vi kan filosofisk diskutere om vi adderer objektene eller antallene, men i praksis gjør vi dette ofte. Vi kan addere epler 🍎.
Adderer vi to epler 🍎🍎 og tre epler 🍏🍏🍏 kan det være fristende og tidsbesparende å si “2+3” uten å nevne eplene. Noen ganger kan dette også være formålstjenlig for å abstrahere oss vekk fra det konkrete. Men ofte er det bra, og vel så riktig, å si hva vi adderer: “To epler pluss tre epler”. Da beholder elevene forbindelsen til det konkrete. Matematikken blir en modellering av virkeligheten ellers, ikke bare løsrevet teori. Det kan understøtte både motivasjon og læring. Det hjelper dessuten til å vurdere rimeligheten av svar.
Tilsvarende er praktiske problem ofte knyttet til enheter. Vi adderer 2.0 kg og 3.0 kg. Da kan det være raskest å si og skrive bare “2.0 + 3.0”. Ofte er det både bra og riktig å si også enhetene: “2.0 kg + 3.0 kg”. Det tar litt lengre tid å si, men den tida trenger elevene på å oppfatte det læreren sier uansett; og dette er enklere for elevene å forstå.
Det er forskjell på 2 kg, 2 gram, 2 meter og to epler.
Oppgaver#
5−3 blir .
7−4 blir .
9− blir 4.
5−4 blir .
5−−4 blir .
5−−−4 blir .
6−−2 blir .
−3−4 blir .
−4−−5 blir .
6 minus -4 blir
1 + 2 + 3 blir .
1 − 2 − 3 blir siden vi tolker subtraksjon .
Talltyper#
Man kan subtrahere to naturlige tall (telletall). Da kan man få et negativt tall! Subtraksjon åpner altså en ny talltype!
Aspekter#
Tankemodeller#
Dette er eksempler på det vi vil kalle to tankemodeller. Tankemodellene er naturlig å representere på forskjellige måter; men de gir lik matematikk (minus).
For elever kan “forskjell” og “trekke fra” se ut som to forskjellige ting. Det må vi ta hensyn til, selv om voksne er vant til å tenke på “minus” som én ting. Det å ha to tankemodeller er også en ressurs: Modellene kan inspirere til hver sine algoritmer.
Senere skal vi se at også divisjon (deling) kommer av to tankemodeller: Målingsdivisjon og delingsdivisjon.
(Subtilt poeng TODO: Symmetri)#
Er forskjell orientert mer mot å sammenlikne to likeverdige (symmetriske) ting, mens å fjerne er å fjerne noe fra noe annet (usymmetrisk)? Kan vi snakke om tilsvarende i addisjon: Å (symmetrisk) legge sammen to symmetriske ting vs. å (usymmetrisk) legge noe til noe annet? Er den simple algoritmen mer symmetrisk orientert, mens å “telle fra den ene addenden” mer usymmetrisk orientert?