Brøk#
Forutsetninger og læringsmål#
Tidliger har vi introdusert
operasjonene addisjon, subtraksjon, multiplikasjon og divisjon. Brøk har særlig sammenheng med divisjon.
talltypene naturlige tall, heltall og relle tall. Nå skal vi særlig jobbe med naturlige tall (i teller og nevner) og reelle tall (som brøkens verdi).
Vi skal nå introdusere en ny talltype: Brøk. Vi kan addere, subtrahere, multiplisere og dividere brøk.
Dette er mye greier! Dette kapitlet har som mål å vise deg både at brøk er vanskelig og at det er lett.
I brøk er det tydelig at det er viktig med gode representasjonsspråk. Mange vanlige misoppfatninger oppstår fra instrumentelt arbeid med formelspråket uten at elevene ser brøker i grafiske representasjoner.
De fleste av pilene i fagkartet over er av typen “inni-algoritme”; en algoritme (f.eks. samle brøk) må læres før en annen (f.eks. addisjon av brøk) fordi den brukes som inni-algoritme i den andre.
Hvorfor bryr vi oss om brøk?#
Brøk er et favoritt-tema for mange matematikere, særlig matematikk-lærere. Brøk får en plass som er mye større enn det man kunne forvente av bruk i dagliglivet. Hvorfor synes de dette er interessant?
Et viktig svar er at brøk er en forberedelse mot algebra. Så lenge vi jobber med heltall og desimaltall og de fire “grunnleggende regneartene” (+, −, ÷ og ×) kollapser regnestykkene raskt til tallverdier. Når vi begynner med brøk kommer utfordringer som gir oss nye strukturer. Disse strukturene skal bli viktig i videre arbeid med algebra. Forberedelse til parenteser. TODO skrive bedre
Læreplanen#
- 6. klasse: formulere og løse problemer fra sin egen hverdag som har med desimaltall, brøk og prosent å gjøre, og forklare egne tenkemåter
- 7. klasse: utvikle og bruke hensiktsmessige strategier i regning med brøk, desimaltall og prosent og forklare tenkemåtene sine
- 7. klasse: representere og bruke brøk, desimaltall og prosent på ulike måter og utforske de matematiske sammenhengene mellom disse representasjonsformene
- 8. klasse: utforske og beskrive primtallsfaktorisering og bruke det i brøkregning`. Dette er særlig relevant i brøksamling.
Mesteparten av femte klasse går til brøk. Men brøk, brøkproblemer og brøkbruk er aktuelt langt oppover i klassetrinnene. Det hender forståelsen av brøk svikter også på grunnskolelærerutdaningen, og da blir det vanskelig å lære mer avansert matematikk.
Referanser#
Realfagsløyper.no (fra matematikksenteret) Ungdomsskolen→Vurdering og tilpasset opplæring → Pakke 3: Misoppfatninger i matematikk → Modul 5: Misoppfatninger knyttet til brøk
Kristian Alfsvåg har laget en videoforelesning om brøk. Gi gjerne tilbakemeldinger!
Matematikksenteret aktivitet: Hannes blomsterbed og Kaker i kakeboksen
[Hinna, Rinvold, and Gustavsen, 2016] 1.5 s117
Introduksjon#
Wiggo har to roser 🌹🌹 som han vil dele på tre buketter  . Hvor mange roser blir det i hver? Det skal være like mange i hver bukett.
. Hvor mange roser blir det i hver? Det skal være like mange i hver bukett.
Brøk er veldig lite romantisk. Her kan vi snakke om halve roser og tredels roser.
Mange elever har en forforståelse av ord som “halve” og “kvarte”.
I praktisk arbeid med barn er det ofte praktisk å gjøre tilsvarende med fyrstikker. Fyrstikker kan brekkes.
Denne introduksjonen var med et eksempel: Vi gjorde en handling fra dagliglivet i en dagligdags representasjon.
Delene må være like!#
Det er så viktig at delene er like at vi koster på oss en tegneserie for å illustrere hva som kan skje om man deler ulikt:

Noe dypt om å plassere i enheter her?
Introduksjon 2: Tall-linje#
Brøk kan også introduseres på en tall-linje. Da bruker vi et kjent rom for eleven, og påpeker at rommet (representasjonsspråket) tall-linje har potensiale for mer enn heltall.
Introduksjon 3: Fra deler (teller og nevner)#
Man kan også introdusere brøk ved å si at en brøk består av en teller og nevner. Her introduseres en brøk med delene, på en måte som er naturlig i formelspråket. Men denne måten å introdusere på gir lite innsikt i hva en brøk egentlig er!
Representasjoner#
Ord#
Vi kaller slike tall for brøk. Ordet har sammenheng med “brekke” og engelsk “break”.
På svensk sier man “bråk”, og det kan være et malerisk uttrykk for vanskelighetene mange elever forbinder med temaet. En del elever mister matematikken når de kommer til brøk: Men som alltid: Gode representasjoner er nødvendige for å mestre et tema.
En brøk består av en teller og en nevner. I \(\frac{2}{3}\) er 2 teller og 3 nevner. 2 teller hvor mange tredeler vi har, og tre nevner hva slags deler vi har. Vi har altså \(\frac{\textrm{teller}}{\textrm{nevner}} = \textrm{brøk}\).
I offisiell norsk skal man si kardinaltall for teller og nevner: to tre-deler. I muntlig sier mange ordinaltall for nevneren: to tredje-deler. Språkrådet tillater dette for nevnere opp til tolv. Språkrådet mener ellers man skal ha éntall av enheter etter brøk (fem tredelers side) men flertall etter desimaltall (to komma fem sider). Disse dokumentene følger ikke alltid Språkrådets anbefalinger.
En del brøker har spesielle navn: Halv, kvart, halvannen. Også en del andre ord kan assosieres med omtrentlige brøker: Litt, mesteparten, alt.
Formelspråk#
Brøk skrives ofte med telleren over en brøkstrek og nevneren under (\(\frac{2}{3}\)). Noen ganger blir brøkstreken satt litt på skrå (\(^2/_3\)) eller helt på skrå (\(2 / 3\)). I Unicode finnes egne tegn for mange brøker (⅔). Disse skal vi regne som typografiske skrivemåter for nøyaktig det samme.
Vi skal derimot gjøre forskjell på en brøk (\(\frac{2}{3}\)) og det tilsvarende divisjonsstykket (2÷3).
Det kan være utfordrende å skrive inn brøker effektivt, fordi brøker står “over hverandre” og ikke bare er tegn på rekke. Vi skal senere diskutere måter å skrive formler på. Nå nevner vi bare kort noen alternativ, med eksempelet ⅔:
Syntaksen
2 / 3; fungerer i mange sammenhenger, enkelt å skrive, gir middels resultatWord/MS Office formeleditor: når man har Office tilgjengelig, veldig tungvint å skrive, gir ganske bra resultat
Word/MS håndskriftgjenkjenning: når man har Office og håndskriftsinput tilgjengelig.
Skriv på ark, ta bilde med mobilkamera, lim inn i f.eks. Word! Gir bra nok resultat til f.eks. arbeidskrav og eksamen.
Mer avanserte ting, se her.
Småstein: Steinbiter#
Vi skal nå utvide småsteinmetaforen. Vi har definert at “1” representerer det samme som “ ”. Vi skal definere at “1” delt i to, altså ½, representerer det samme som
”. Vi skal definere at “1” delt i to, altså ½, representerer det samme som  . Når vi tegner brøker, blir det lett smått, så vi skal forstørre litt:
. Når vi tegner brøker, blir det lett smått, så vi skal forstørre litt:  og
og  . ⅖ representeres som
. ⅖ representeres som  .
.
Vi har nå gjort noen forandringer:
Vi tegner en svart ramme rundt hver
 er.
er.Vi tegner tynne linjer mellom hver del. De tynne linjene indikerer altså nevneren. Nevneren er antall små områder med tynne streker mellom. Disse småområdene skal være like store.
Farge indikere telleren. Telleren er antall småområder som er farget.

Fig. 8 Med fare for dårlig humor: Steinbit. Stygge bilder og teite huskeregler er egnet til å skape følelser og kan derfor hjelpe oss til å huske.#
En tredel (⅓) tegnes som  delt i tre deler hvor 1 av delene er fargelagt:
delt i tre deler hvor 1 av delene er fargelagt:  . Har vi to tredeler tegner vi
. Har vi to tredeler tegner vi  .
.  (en tredel) pluss
(en tredel) pluss  (to tredeler) blir
(to tredeler) blir  (tre tredeler) som er det samme som
(tre tredeler) som er det samme som  . Seks tredeler blir
. Seks tredeler blir  , som er like mye som
, som er like mye som  (2).
(2).
Siden dette handler om biter av småstein, kan vi kalle dette for steinbit-representasjonen.
Vi har tidligere representert minus to som  . Negative steinbiter kan representeres på flere måter. Minus to femdeler kan for eksempel representeres som
. Negative steinbiter kan representeres på flere måter. Minus to femdeler kan for eksempel representeres som  .
.
Fliser (sjokoladekaker)#

Fig. 9 Sjokoladekake fra Det glade kjøkken#
Flisrepresentasjon trenger vi når vi jobber med multiplikasjon, divisjon og liknende. Vi skal introdusere multiplikasjon og divisjon av brøker nedenfor, men tyvstarter her med noen eksempler.
Vi har tidligere sagt at  er en annen skrivemåte for
er en annen skrivemåte for  . På samme måte er
. På samme måte er  en annen skrivemåte for
en annen skrivemåte for  .
.
Vi skal nedenfor se at ½×⅓ kan representeres som  . Svaret er \(\frac{1}{6}\); ser du telleren 1 og nevneren 6 i flisrepresentasjonen? Hva skjer om regnestykket er ½×⅔?
. Svaret er \(\frac{1}{6}\); ser du telleren 1 og nevneren 6 i flisrepresentasjonen? Hva skjer om regnestykket er ½×⅔?
Noen ganger brukes ordet sjokoladekakespråket. Vi snakker da om firkantede sjokoladekaker som kan deles opp.
Sektor-representasjoner (bløtkaker)#
Et annet tradisjonelt representasjonsspråk er sektordiagram, også kalt kakediagram, bløtkakediagram eller pizzadiagram). Her er  ⅗ representert som del av en sirkel:
⅗ representert som del av en sirkel:
 . Fem tredeler
. Fem tredeler
 er litt mer enn én:
er litt mer enn én:
 I sektordiagram deler vi altså en sirkel opp i like mange sektorer (kakestykker) som nevneren, og fargelegger like mange sektorer som telleren.
I sektordiagram deler vi altså en sirkel opp i like mange sektorer (kakestykker) som nevneren, og fargelegger like mange sektorer som telleren.
Sektordiagram er vanlig, men har noen viktige ulemper, som vi her bare påstår uten begrunnelse:
Forsøk viser at folk er dårligere til å anslå størrelse på bløtkakestykker enn på sjokoladekakestykker.
Det er vanskeligere å multiplisere bløtkaker enn sjokoladekaker.
Vi skal derfor oftest velge sjokoladekaker framfor bløtkaker. Selv om bløtkaker også er godt.
Tall-linje#
Tall-linje-representasjoner er sjeldnere brukt når vi snakker om brøk, men vi skal se på det for kompletthetens skyld.
Tallet en kan vi tegne som et punkt
 eller som et intervall
eller som et intervall
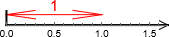 . Dette intervallet kan vi dele i tre
. Dette intervallet kan vi dele i tre
 . Den første av disse tre-delene kommer til et punkt på linja mellom 0 og 0.5
. Den første av disse tre-delene kommer til et punkt på linja mellom 0 og 0.5
 . Zoomer vi inn, ser vi at punktet ligger mellom 0.3 og 0.4:
. Zoomer vi inn, ser vi at punktet ligger mellom 0.3 og 0.4:
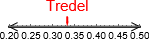 (se nøye på merkelappene under linja). Det viser seg at punktet er nær 0.333.
(se nøye på merkelappene under linja). Det viser seg at punktet er nær 0.333.
Et annet tall, to tredeler, er nær 0.667
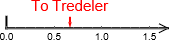 .
.
Algoritmer#
Her følger algoritmer for å lage brøk. Videre skal vi også forklare mange andre algoritmer som har med brøk å gjøre (for eksempel addisjon av brøk).
Delingsdivisjon#
Vi har introdusert brøk med en regnefortelling (Wiggos to roser delt i tre buketter); denne er essensielt om delingsdivisjon.
Målingsdivisjon#
En fortelling som modellerer 2÷3 som målingsdivisjon kan være: To roser skal deles i buketter hvor det er tre roser i hver bukett; hvor mange buketter får vi?
Divisjon og brøk#
En brøk \(\frac{a}{b}\) hvor \(a\) og \(b\) er naturlige tall kan alltid gjøres om til en divisjon \(a÷b\) og omvendt: \(\overset{\frac{a}{b}}{\underset{a÷b}{⇵}}\)
Talltyper#
ℚ Rasjonale tall#
Vi har tidligere sagt at rasjonale tall (ℚ) er resultatet av en divisjon. En vanligere, helt ekvivalent, definisjon er å si at rasjonale tall er tall som kan skrives som brøk.
Rasjonale tall har symbolet ℚ. Huskeregel: Quotient.
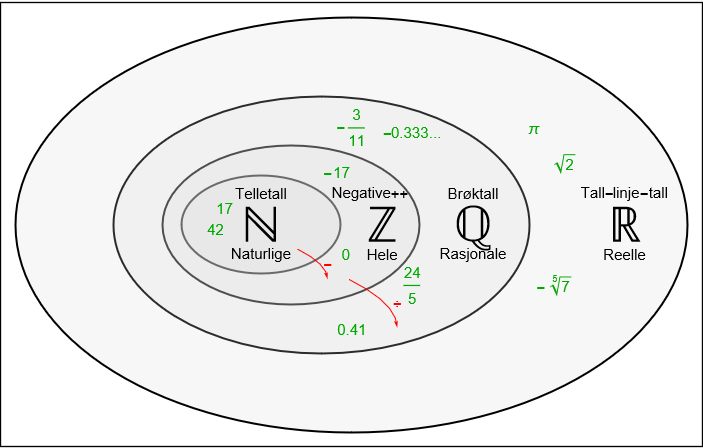
Senere skal vi bevise at det finnes reelle tall (på tall-linja) som ikke kan skrives som brøker. Dette er kanskje overraskende. Eksempler er π og √2.
Rasjonale tall og desimaltall#
Vi har riktignok ikke introdusert desimaltall ennå, men tar med et par kommentarer:
De fleste rasjonale tall (altså de fleste brøker) kan skrives som desimaltall (som vi riktignok ikke har introdusert ennå) i titall-systemet, men ikke alle: ⅓ og ⅐ kan ikke skrives som desimaltall.
Alle desimaltall i titall-systemet kan skrives som rasjonale tall. 123.45 kan for eksempel skrives som 1·10² + 2·10¹ + 3·10⁰ + 4·1/10 + 5·1/100, eller om man vil \(\frac{12345}{100}\).
Mengden av alle desimaltall er altså mindre enn ℚ.
Aspekter ved brøk#
Man kan snakke om ulike aspekt ved brøk:
Brøk som tallverdi
Brøk som del av helhet
Brøk som operator
Brøk som divisjon
Brøk som måling
Brøk som forhold
Er dette samme som det vi har kalt tankemodeller≈verb for subtraksjon og divisjon? Hva med aspektene for variabel?
Typer brøker#
Stambrøker er brøker med teller 1, altså \(\frac{1}{}\): ½, ⅓, ¼ og så videre.
Ekte brøker har verdi mellom 0 og 1. Uekte brøker har verdi ≥ 1.
Blandet tall er en representasjonsform i formelspråket som burde vært forbudt. Det er utdatert, og fører bare til forvirring hos elever og datamaskiner. Vanligvis skal ab tolkes som a·b; hvorfor skal 2¾ tolkes som 2 + ¾?
Pedagogiske aspekt#
Misforståelser#
Søk etter “misforståelser brøk”. Mange er knyttet til ensidig bruk av formel-representasjon.
Prosesser#
Sjekke med desimaltall (iallfall omtrentlig)#
Ofte når vi skal sjekke om et regnestykke med brøk er riktig, kan vi regne om til desimaltall og sjekke om det blir riktig da. I stedet for ½ + ½ kan vi si 0.5 + 0.5. Vi kan også regne om til et omtrentlig desimaltall: I stedet for ⅓ + ⅓ kan vi si 0.3 + 0.3, og finne ut at det vi kom fram til (⅔) var omtrentlig riktig (0.6).

