Prosent#
Forutsetninger og læringsmål#
Tidligere har vi introdusert brøk. Nå skal vi jobbe med én spesiell type brøk, nemlig hundredeler. Dette er mye brukt i samfunnet. Prosent er ofte forbundet med formlene \(andel = \frac{del}{helhet}\), \(ny = gammel + økning\) og gjentatt vekst.
Læreplan#
- 6. klasse: formulere og løse problemer fra sin egen hverdag som har med desimaltall, brøk og prosent å gjøre, og forklare egne tenkemåter
- 7. klasse: utvikle og bruke hensiktsmessige strategier i regning med brøk, desimaltall og prosent og forklare tenkemåtene sine
- 7. klasse: representere og bruke brøk, desimaltall og prosent på ulike måter og utforske de matematiske sammenhengene mellom disse representasjonsformene
Oppgaver#
Ndla prosentregning. Vekstfaktor. Prosentfaktor se også fra 1P
Matematikksenterets læringsressurser for relevante kompetansemål (6. og 7. trinn), f.eks. Tre-på-rad (er mulig å gjøre også for studenter!)
[Hinna, Rinvold, and Gustavsen, 2016] 1.6.1 s154, oppgaver s158
Introduksjon#
Eksempel#
Sara skal kjøpe kjole på salg. Hele prisen på kjolen er i utgangspunktet 200 kroner, men hun får 40% rabatt. Hvor mye må hun betale?
Hovedide#
Centurion Felix Platypus opptrer i “Asterix and the Roman Agent”. En centurion er sjef over soldater.
Antall centi-meter i en meter er .
I romertall står tallet Ⅽ for .
Centi betyr altså hundre. Pro-sent (engelsk: per-cent) betyr for hver hundre. En prosent er en hundredel. \(\frac{1}{100}\) som desimaltall er .
25% er selvfølgelig \(25·\frac{1}{100}\) som blir \(\frac{25}{100}\) som kan forkortes til \(\frac{1}{4}\).
Når vi regner med prosent er det viktig å vite hva vi tar prosent av / hva som er helheten.
Representasjoner#
Ord#
På norsk sier vi prosent. Vi kan bruke prosenttegnet også når vi skriver tekst — vi trenger ikke skrive ordet prosent med bokstaver. På norsk skal vi egentlig ha mellomrom mellom måltallet og prosenttegnet (20<mellomrom>%). I språket brukes prosent nesten som en enhet (som meter eller m).
På engelsk brukes percent eller percentage: The percentage is twenty percent.
Senere skal vi komme til uttrykket prosentpoeng. Dette brukes egentlig til å si hva vi tar prosent av (hva som er det hele). Det kan tenkes at FrP har steget med nitti prosent, men har steget med bare tre prosentpoeng.
Formelspråk#
I matematiske formler bruker vi prosenttegnet %, som betyr det samme som \(\frac{1}{100}\). \(20\;%\) betyr altså det samme som \(20·\frac{1}{100}\) som er lik .
Prosenttegnet kommer av italiensk per cento, hvor per er forsvunnet og cento gradvis på 1400‒1600-tallet ble til to sirkler med en vannrett linje. Den siste sirkelen er altså egentlig o-en i “cento”, men vi kan bruke de to sirklene som en huskeregel om de to 0-ene i 100.
Tall-linje#
Prosentverdier kan tegnes inn på tall-linja. For eksempel kan 25% representeres som
. Sammenlikn dette med
(altså 0.25) og
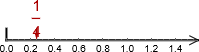(altså ¼). Dette er representasjoner av tall som har samme tallverdi.
En negativ prosentverdi, for eksempel −30% som er desimaltall , kommer til venstre for 0:
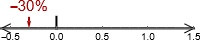. 150% er lik og kommer til høyre for 1:
.
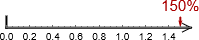Småstein#
Småstein-, steinbit- og flismetaforene går egentlig i ett. Vi ønsker oss nå å representere også prosent-tall i denne metaforen. Vi kunne tenke det er naturlig å representere for eksempel 25% som \(\frac{25}{100}\); problemet er at de svarte tynne linjene ville gjøre representasjonen helt uleselig: 
. Vi skal derfor droppe de tynne linjene, men ellers bruke samme representasjon. 25% blir da
. Sammenlikn dette med 
(altså
/). Legg merke til at vi markerer nøye, med boksen 
, hva som er
.
200% representerer vi som
, som kan sammenliknes med
.
125% representerer vi som
; det er litt større enn det hele, og kan sammenliknes med
(brøken \(\frac{5}{4}\)). Verdien er den samme.
−74% kan vi vi som 
. Vi kan også bruke en strek over 
TODO
Vi ser at denne utvidelsen bygger naturlig videre på småsteinspråket. Prosent-tall som har samme verdi som en heltall og brøk får en representasjon som viser dette. Det viser seg at også de fire regneartene fungerer naturlig. Vi tar med to eksempler:
Addisjon: 2 + 50% + 25% + 1/4 er
som er 
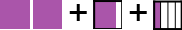som er 
.Multiplikasjon: 3·25% er
som er 
og (altså 75%).
Sektordiagram (bløtkaker)#
Akkurat som for brøk har det også vært vanlig å representere prosenter med sektordiagram: 50% blir
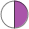mens 25% blir
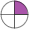
Det finnes altså innvendinger mot bløtkaker som gjør at vi foretrekker sjokoladekaker. Sjokoladekaker er enklere å lese presist og de er enklere å multiplisere.
Vi vil derfor rbuke mindre krefter på denne representasjonen. Av kulturelle årsaker bør likevel elevene (og studentene) likevel gjenkjenne noen vanlige brøkverdier også som sektordiagram:
TODO tabell
Regneark#
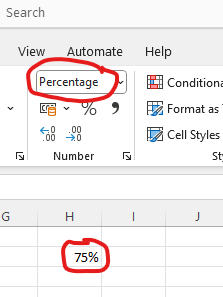
Skal man representere et prosent-tall som 75% i regneark (for eksempel Excel, Google Sheets eller LibreOffice Calc) bør man skrive inn 75% eller 0.75, ikke 75. Tallverdien 75% er som kjent det samme som 0.75, men noe helt annet enn 75.
Så kan man formatere tallet som “Prosent” (“Percentage”). Dette skjer automatisk når man skriver 75% inn i en celle; tallverdien blir lagret som 0.75, men formateringen blir satt til prosent.
Det er et vanlig problem når man overtar regneark at folk har skrevet 75 når de mener 75%.
Aspekter ved prosent#
Man kan snakke om ulike aspekt ved brøk: Brøk som tallverdi, brøk som del av helhet, brøk som operator, brøk som divisjon, brøk som måling og brøk som forhold. Tilsvarende kan man snakke om om aspekter ved prosent. Noen ganger møter man også påstander om at brøk eller prosent “i virkeligheten er” ett av aspektene.
Ulike representasjoner antyder muligens forskjellige aspekter: kanskje tall-linja antyder brøk som tallverdi, mens andre antyder brøk som forhold mellom andre tall. Ord som “halv(parten)” antyder kanskje at noe er halvparten av en helhet.
Også andre tall kan ha forskjellige aspekter. Ordet “dobbelt” antyder kanskje forhold, i og med at man er dobbelt av noe.
I vår matematiske tradisjon er det kanskje vanligst å forbinde heltall med tellbar mengde, brøk som forhold og prosent som del av en helhet.