Den distributive lov#
Forutsetninger og læringsmål#
Den konkrete versjonen at × er distributiv over + bruker vi ofte.
Dette trenger vi generelt for ringer.
Introduksjon#
Mens den kommutative lov og den assosiative lov omhandlet én operator (kalt ⊕), omhandler denne distributive to operatorer, som vi kaller ⊕ og ⊗.
Generelt er den distributive lov \(\overset{a ⊗ (b ⊕ c)}{\underset{a ⊗ b ⊕ a ⊗ b}{↓}}\).

Fig. 23 3 × 12
3 × (10 + 2)
3×10 + 3×2
30 + 6
36#
Det prototypiske eksempelet er at × er distributitiv over +: \(\overset{$a × (b + c)}{\underset{a × b + a × b}{↓}}\). Vi har altså for eksempel at \(\overset{4×(10 + 3)}{\underset{4×10 + 4×3}{↓}}\), altså at \(\overset{4×(13)}{\underset{4×10 + 4×3}{↓}}\).
Representasjoner#
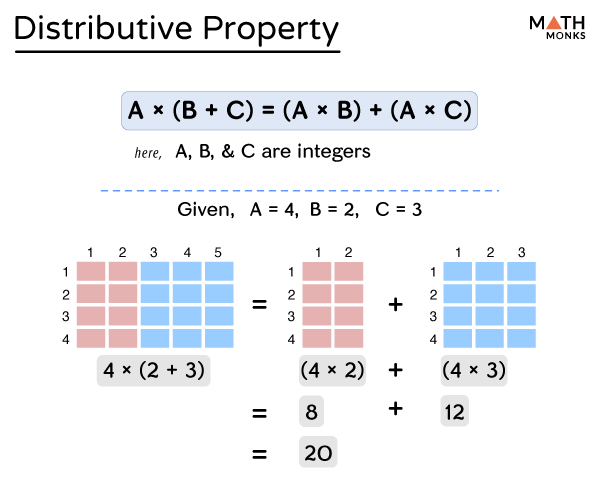
Fig. 24 Fra mathmonks.com#
Algoritmer#
Å avgjøre om en operator er distributiv over en annen#
Oppgaver
Er + distributiv over ×?
Løsningsforslag
Nei, det stemmer aldeles ikke at \(a + (b × c) ↔ a+b × a+c\). Om dette er vanskelig å se direkte kan vi prøve med et eksempel (si {a ↦ 2, b ↦ 3, c ↦ 4}: 2 + (3×4) blir 24 mens 2×3 + 2×4 blir 12.
Er ^ (potens) distributiv over ×?
Løsningsforslag
Nei, det stemmer ikke at \(a^{b × c}\) er det samme som \(a^b × a^c\).
Er union distributiv over snitt? (dette kan vises f.eks. med sannhetsverditabell eller Venn-diagram).
Er snitt distributiv over union?
