Faktorer#
Forutsetninger og læringsmål#
Vi skal introdusere faktorisering og primtall. Handler på en måte om å dele opp tallet — ikke additivt men multiplikativt. Vi går for eksempel fra 12 til 2×2×3.
Repetisjon#
I en multiplikasjon har vi at faktor × faktor = produkt. For eksempel har vi at  (altså 2×3) er
(altså 2×3) er  (6). I multiplikasjon vet vi faktorene og skal finne produktet. Det representerer vi med bakgrunnsfarge
(6). I multiplikasjon vet vi faktorene og skal finne produktet. Det representerer vi med bakgrunnsfarge  på resultatet og med å sette det nederst til høyre.
på resultatet og med å sette det nederst til høyre.
Oppgaver#
Referanser#
[Hinna, Rinvold, and Gustavsen, 2016] 1.4.4 Divisjon
Introduksjon#
Se på alle heltall fra 1 til 20. Hvilke av dem kan legges som et rektangel hvor sidene er mer enn 1?
Årstallet 2022 kan skrives som regnestykket 2×3×337. Faktorene i 2022 er {2, 3, 337}. Disse faktorene kan vi ikke skrive som produkt av to naturlige tall (utenom 1 og seg selv, da), og vi kaller dem primtall.
Faktorisering#
Å faktorisere et tall a er å finne to naturlige tall (faktorer) som multiplisert blir a. Skal vi faktorisere tallet 6 kan vi finne faktorene 2 og 3.
Faktoren 1 er uinteressant: å faktorisere 6 til faktorene 1 og 6 blir ikke regnet som faktorisering.
Representasjoner#
Ord#
Vi kan multiplisere faktorer og få et produkt. Å faktorisere er å begynne med et produkt og finne faktorer.
Ordforklaring: Faktor
Latin facio betyr å gjøre eller lage. Factus betyr gjort eller laget; factor noe som gjør eller lager. I moderne språk er en faktor både en del av og noe som bygger opp. Tenk også på faktum, som egentlig betyr noens gjerning. I gamle dager kunne faktum bety resultatet av multiplikasjon av to faktorer. Også relatert til -fikk som i spesifikk.
Formelspråk#
Vi har ikke noe tradisjonelt symbol for faktorisering. I dette dokumentet vil vi noen ganger bruke symbolet 🪓, altså en øks, siden faktorisering på en måte er å dele opp tallet.
Fliser#
Faktorisering#
Skal vi faktorisere et tall (f.eks. 6) må vi finne dets faktorer (f.eks. 2 og ). Regnestykket faktor × faktor kan da representeres i flis-språket så produktet blir et rektangel. Å faktorisere et tall er altså å legge i rektangel.
Skal vi faktorisere  , må vi splitte opp
, må vi splitte opp  eren til
eren til  ere. Da kan vi legge det som
ere. Da kan vi legge det som  , med faktorene
, med faktorene  og
og  . En annen mulighet er
. En annen mulighet er  , med faktorene
, med faktorene  og
og  .
.
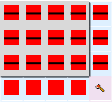
Et mer komplisert eksempel: 🪓  (altså 132) kan for eksempel legges i rektangel som
(altså 132) kan for eksempel legges i rektangel som  med faktorene
med faktorene  og
og  .
.
Lover#
Talltyper#
Faktorisering#
Når vi snakker om faktorisering, snakker vi vanligvis om heltall eller bokstavuttrykk, sjelden om reelle tall. Maksimum én av faktorene er negative.
 ,
,  ,
,

TODO også andre bokstavuttrykk

