Den kommutative lov#
Forutsetninger og læringsmål#
Vi snakker om den kommutative lov for addisjon: \(\overset{a + b}{\underset{b+ a}{⇵}}\) og multiplikasjon: \(\overset{a × b}{\underset{b × a}{⇵}}\).
- 2. klasse: utforske den kommutative og den assosiative egenskapen ved addisjon og bruke dette i hoderegning
- 3. klasse: bruke kommutative, assosiative og distributive egenskaper til å utforske og beskrive strategier i multiplikasjon
Denne siden handler om den kommutative lov for addisjon og multiplikasjon. Vi skal senere snakke generelt om kommutativitet for andre operatorer.
Introduksjon fra addisjon#
I småsteinrepresentasjonen er det klart at 
er like mange som 
. Addendenes rekkefølge er likegyldig. Vi kan jo bare bruke algoritmen “flytte småsteinene (altså 
erne) rundt omkring”. Algoritmen blir et bevis for regelen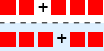 
, altså \(\overset{2 + 3}{\underset{3 + 2}{↓}}\).
Tilsvarende regel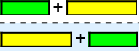 
(altså \(\overset{a + b}{\underset{b + a}{↓}}\)) gjelder for hvilket som helst tall \(a\) og \(b\). Dette beviser vi ikke formelt nå, men det virker opplagt i småsteinrepresentasjonen. Dette er en generell regel som gjelder for mange tall (faktisk for uendelig mange tall \(a\) og \(b\)).
Denne innsikten kalles den kommutative loven for addisjon.
Ordforklaring: Kommutativ
En huskeregel for navnet “kommutativ” er “commute” i trafikken (en buss som går fram og tilbake).
Et eksempel på bruk av kommutativ lov er regnestykket 2 + 7. En elev kan selvfølgelig bruke en simpel algoritme, telle opp 
og 
og legge sammen. Det er enklere å bruke kommutativ lov til å få 7 + 2 og telle fra første addend: 7,8,9. Dette gjelder enda mer om vi har oppgaven 2 + 57. Da kan vi si
.
Dette er altså en egnet strategi når første addend er liten og den andre stor.
blir 3 + 83 blir
4 + 61 blir .
Representasjoner#
Om vi har gode representasjoner er kommutative lover mer eller mindre selvfølgelige. Det kan man egentlig si om de fleste lover og algoritmer. Med dårlige representasjoner er de kronglete.
Småstein#
Algoritmer og operatorer#
Addisjon#
Subtraksjon#
Nei! Men noen elever kan tenke at det gjelder. Motbevises enklest med moteksempel.