Andel = del / helhet#

Forutsetninger og læringsmål#

Introduksjon#

Sara skulle kjøpe ny kjole. Den kostet i utgangspunktet 200 kroner, men hun måtte nå betale 160 kroner.

I noen land sier man at om noen kjører mindre enn ti prosent over fartsgrensa, får de ikke bot. I et slikt land skiftet de nylig ut alle fartsgrensene fra miles/h til km/t. Hva blir den nye tommelfingerregelen? [Mason et al., 2010] Speed trap, p. 175

Hamburgere består av brød, tomat, salat og kjøtt. Om prisen på hver av ingrediensene øker med 5%, hvor mye øker prisen på hele hamburgeren? [Mason et al., 2010] Hamburgers, p.189

Representasjoner#

Representasjoner#

Grafisk#

Situasjonen over kan representeres som

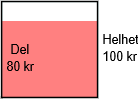
Denne grafikken er ment å spille på lag med tidligere representasjoner av brøk og prosent. Vi repeterer at
⅘ kan representeres med eller og at
80% kan representeres med eller .

Et viktig element er den svarte ramma. Den er ikke til pynt; den illustrerer helheten.

Ord#

Vi snakker her om tre begrep:

  • Helheten er for eksempel 200 kroner. Den kalles noen ganger opprinnelig pris, det hele, utgangspunktet eller liknende; men det er ikke alltid helheten kommer “tidligere” enn delen. Helheten har ofte en enhet, for eksempel “kroner”.

  • Delen er for eksempel 160 kroner. Den har samme enhet som helheten.

  • Andel er for eksempel 80%, ⅘ eller 0.8. Dette er et forholdstall, uten enhet/benevning. Dette er forholdet mellom det røde området og den svarte ramma i tegningen over. Den kan uttrykkes som prosent, brøk eller desimaltall, og kan også kalles prosentandel.

Formelspråk#

Vi har da formelen \(andel = \frac{del}{helhet}\). Strengt tatt har vi riktignok ikke introdusert likninger ennå. Denne likningen har altså tre størrelser. Vet vi av dem kan vi alltid finne den tredje.

Trekant-huskeregel#

Noen liker å sette opp en trekant som huskeregel:

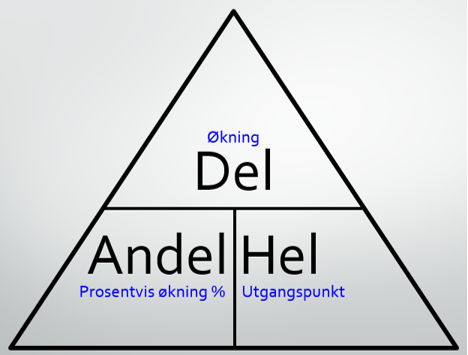
Dette er ment som huskeregel på om man skal gange eller dele; man holder handa foran det man skal finne, og de to andre størrelsene kommer fram som et gangestykke (\(andel × helhet\)) eller delestykke (\(\frac{del}{andel}\) eller \(\frac{del}{helhet}\)).

Personlig spør jeg om dette er noe enklere enn å forstå formelen \(andel = \frac{del}{helhet}\) og så bruke enkel likningsmanipulasjon.

Prosent og prosentpoeng for å klargjøre helheten#

Noen ganger, hvor det er uklart hva som er helheten, kan vi bruke ordet prosentpoeng for å klargjøre. Standardeksempelet er politiske meningsmålinger, for eksempel at et parti forrige måned hadde en oppslutning på 4 prosent, men nå har steget til 6 prosent. Økningen er jo da 50 prosent, om vi setter “helheten” som forrige måneds verdi. Men partiet vi sier at partiet har økt med to prosentpoeng. Snakker vi om prosentpoeng regner vi altså “helheten” som noe større (i dette tilfellet: alle stemmeberettigede).

  • Om et parti går fra 10 til 12 prosentpoeng har det økt med prosent.

  • Om et parti har 20 prosent oppslutning men synker med 25%, ender det på prosent opplslutning. Det har da sunket med prosentpoeng. Vi kunne nok sagt at partiet gikk fra 20 prosentpoeng til 15 prosentpoeng oppslutning.

Algoritmer#

Algoritmer om andel = del / helhet#

Finne andel fra del og helhet#

Her kan vi finne svaret ved et divisjonsstykke. Noen ganger er det lurt å forkorte først. Enheten blir forkortet i brøken (for eksempel \(\frac{\textrm{kr}}{\textrm{kr}}\) som blir ). Noen ganger ønsker vi å ha svaret som prosenttall eller brøk.

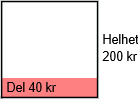  • Om delen er på 40 kroner av en helhet på 200 kroner blir andelen /10, altså desimaltallet , altså %.

  • Om delen er på 30 kroner av en helhet på 40 kroner blir andelen /4, altså desimaltallet , altså %.

Finne del fra andel og helhet#

Skal vi finne delen, kan vi skrive om vår formel til \(del = andel·helhet\). Om andelen er 40% av en helhet på 200 kroner blir delen 40%·200 kroner som er lik 8000%kr eller \(\frac{40·200 kroner}{100}\) som er lik 80 kr.

Også her kan vi snakke om å dele på 100%, men ikke om å dele på 100.

oppgaver

Finne helhet fra del og andel#

En jakke fikk rabatt på 200 kroner etter å ha vært satt ned 20%; hva var førprisen?
Noen ganger kommer helheten "før" delen.

Det er flere gode algoritmen vi kan bruke. Ser vi på formelen, kan vi skrive den om til \(helhet = \frac{del}{andel}\). Dermed blir helheten lik \(\frac{200\textrm{kr}}{\frac{20\%}{100\%}}\) som blir 1000 kr.

Noen liker også en teknikk som heter veien om 1%. Her er ideen å først finne ut hva som tilsvarer én prosent. Siden 200 kroner tilsvarer 20 prosent, vil synes noen det er enkelt å se at 1% tilsvarer 10 kr og at 100% tilsvarer 100*10 kr = 1000 kr. Dette kan vi tegne opp slik:

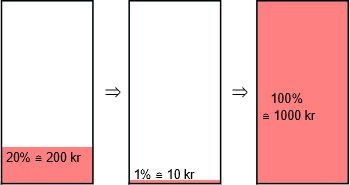
Vi gjentar at tegnet “≘” betyr “tilsvarer”.

  • Om 15% tilsvarer 45 kroner tilsvarer 100% kroner.

Holde styr på helheten#

En vanlig feil#

La oss også se på en utregning som ikke er riktig: 20% av 200 kroner er 40 kroner; 200 kroner + 40 kroner er 240 kroner; altså kostet jakka 240 kroner. (Vi kan se at det er feil fordi 20% av 240 kroner er 48 kroner; ny pris blir da 196 kroner og ikke 1000 kroner.) Hva er feil med tenkemåten?

Problemet er at vi regner 20% av 200 kroner; vi setter altså 200 kroner som helheten. Vi tenker slik:

Helheten er jo det vi skal finne. Vi må tenke
Poenget er at vi må holde orden på hva som er helheten, altså hva vi regner prosent av.

Opp og ned#

Du har 100 kroner og legger til 30 prosent av dette; så trekkes 30 prosent av det nye beløpet. Svaret blir kroner.

Resultatet blir ikke 100 kroner. Poenget er at når vi legger til 30%, legger vi til 30 % av en helhet på 100 kroner. Når vi trekker fra 30%, trekker vi 30% av ny, større helhet:

Oppgaver av denne typen er egnet for å framprovosere tenking rundt helhet.

Ned og ned#

Sara skal kjøpe kjole til eksamen. Den kostet 100 kroner. Hun kan velge mellom å få 50% rabatt og først få 30 % rabatt og så få 20 % til. Hva bør hun velge? Hun bør velge TODO, “først 20% og så 30%”])}} siden nypris ved 50% rabatt er kr og ved 30% og 20% rabatt er kroner.

Også her er hemmeligheten å holde styr på helheten.