Negative tall#

Introduksjon#

Hva med regnestykket 4−6? For eksempel at vi har fire sjokolader og spiser seks?

Dette er i utgangspunktet meningsløst når det gjelder sjokolader. Om Anne har fire sjokolader kan ikke Helene spise seks. Det er også meningsløst i småsteinspråket (iallfall så langt vi har definert det nå). Men det går an å uttrykke i formelspråket, tydeligvis. Det går også an å uttrykke på en tall-linje. Vi er altså på fire og går seks mot venstre:
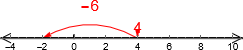og havner på , altså .

Vi kommer til et helt nytt sted hvor vi ikke har vært før. Stedet er like langt fra 0 som det 2 er. Finnes dette stedet? Finnes det slike tall?

Representasjoner#

Vi skal skynde oss å lage flere representasjoner:

  • Formelspråket: “−2”

  • Ord: “minus to”.

  • Eksempelsituasjoner: Ord som “låne”, “mangle”, “ta bort” og “snu”. “kaldt”, “nedover”, “i går”.

  • Småstein: For eksempel . Et stort og interessant spørsmål er hvordan vi best kan representere tallet som småstein.

  • Temperatur- eller termometer-representasjonsspråk. Her ser vi for oss et tradisjonelt termometer som ser ut som en tall-linje, bare loddrett. Her er positive tall representert som “varmt” og “oppover” (på et termometer). Negative tall representeres som “kaldt” og “nedover”.

  • Økonomi: Her assosieres negative tall med “nedover”, “skylde” og “mangle”

  • Fargene rødt/blått kan være forvirrende i vår kultur. Snakker vi om termometre, er ofte rødt assosiert med positive tall og blå med negative. Snakker vi om økonomi, betyr “røde tall” negative tall.

Slike tall skal vi kalle negative tall. Negative tall er mindre enn 0 (teknisk sett har vi ikke introdusert tallet 0 ennå, men vi skal gjøre det snart). Et negativt tall −a er like langt fra 0 som det tilsvarende +a, men på motsatt side. Tallet -3 er like langt fra 0 som er.

Vi brukte altså et representasjonsspråk (tall-linja) og en operasjon (minus) til å finne et helt nytt matematisk objekt (det negative tallet −2). Noe liknende har skjedd flere ganger i matematikkhistorien og i elevers utvikling (Sfard, 1991).

Litt også om representasjon om positive tall: Tallet vi representerer som 5 kan også representeres som +5. Dette er altså to representasjoner av samme tallet; vi veksler mellom dem utifra hva som er praktisk og pedagogisk. Når vi skriver +3 mener vi altså nøyaktig det samme som .

Merk at både +-tegnet og −-tegnet (og faktisk også ordene “pluss” og “minus”) kan brukes på to måter:

  • Infiks, altså mellom operander (eksempel: \(2+5\) og \(2 −5\)). Her betyr tegnene addisjon og subtraksjon.

  • Prefiks, altså i forkant av en operand (eksempel: \(+5\) og \(−5\)). Her betyr tegnene positive og negative tall.

Algoritmer#

Regning med negative tall#

Noen lesere av dette dokumentet kan tenke at regning med pluss, minus og negative tall er en enkel sak. Et av formålene med følgende tekst er å overbevise leseren om at

  • Regning med negative tall er vanskelig, og kan oppleves vanskelig for elevene!

  • Regning med negative tall kan gjøres lett!

  • Det er mange innsikter vi kan få av å studere slik enkel regning, for eksempel om regler, om generalisering og om læring. Disse innsikten skal vi bruke videre seinere.

  • Poenget er egentlig ikke å huske mengder av regler. Poenget er å forstå gode representasjoner, så faller det meste annet på plass av seg selv.

Addisjon#

\(-a + b\)#

Tom skylder fire kroner, men får seks. Hvor mange har han nå? Dette kan vi også representere som eller som −4 + 6. Hver krone Tom skylder () sletter ut en krone Tom har (). Vi kan altså tenke at først sletter ut , og så står det igjen.

Dette kan vi regne ut på tall-linja. Vi starter i −4 og går 6 mot høyre. Vi kommer til +2.

I noen tilfeller kan vi komme til et negativt tall: Tom får ikke nok til å betale lånet. −4 + 2 gir −2.

  • −5 + 10 blir .

  • −8 + 3 blir .

  • −8 + 1 blir .

  • −11 + 2 blir .

\(a + -b\)#

Tom har fire kroner, men får en bot av en politimann på seks kroner. Hvor mange har han nå? Dette kan vi også representere som 4 + −6 eller . Resultatet blir et negativt tall (−2).

Også dette kan vi regne ut på tall-linja.

Noen ganger kan vi komme til et positivt tall: (altså 4 + −2) gir (altså +2).

Subtraksjon og negative tall#

Det å “få” minus seks kroner har samme effekt som å betale seks kroner. 4 + −6 er det samme som 4 − 6. Vi har den generelle regelen \(\overset{a + -b}{\underset{a - b}{↓}}\), hvor \(a\) og \(b\) kan være hvilke som helst naturlige tall (faktisk også andre typer tall).

Likevel: Selv om 4 + −6 har samme verdi som 4 − 6, kan både matematikere og elever tenke på det som to matematiske objekt. Elever kan lære regelen \(\overset{a + -b}{\underset{a - b}{↓}}\) så godt at de vil tenke at \(a + −b\) er likt \(a − b\) og senere at \(a + −b\) er det samme som \(a − b\); til slutt ser de ikke forskjellen. Læringsprosessen kan altså være slik:

  1. En observasjon om to representasjoner har altså blitt til

  2. en prosedyre fra et objekt til et annet, som altså har blitt til

  3. en regel, så til

  4. en likhet, og så har

  5. objektene for eleven smeltet sammen til samme konsept.

\(-a + -b\)#

Tom skylder fire kroner, og får en bot på seks til: (altså −4 + −6 )

Dette blir −10.

-4 + -6 er på en måte motsatt av 4 + 6. På tall-linja blir det representert speilvendt.

Fortsatt har vi at å “få” minus seks kroner er det samme som å betale seks kroner. −4 + −6 er det samme som −4 − 6. Generelt har vi \(\overset{a + -b}{\underset{a - b}{↓}}\); dette er samme regelen som sist, men nå har \(a\) verdien −4 (og \(b\) har verdien 6).

  • −5 + −6 er .

  • −4 + −8 er . Tenkte du noen gang på 4 + 8 som inni-algoritme her?

  • −8 + −5 er .

  • −5 + −1 er . Her var det mulig å bruke en annen algoritme: Telle en og en.

  • −7 + −2 er .

  • −2 + −8 er .

Subtraksjon#

\(-a - b\)#

Vi går nå fra addisjon til subtraksjon:

  • Tom skylder fire kroner, mens Sonja skylder seks. Hvem har flest? Dette er forskjell-subtraksjon.

  • Tom skylder fire kroner, og må betale seks kroner. Hvor mye har han etterpå? Dette er fjerne-subtraksjon.

Dette er to situasjoner som begge må representeres med “−4 − 6” i formelspråket; men tankemodellene er forskjellige.

Vi kan bruke begge tankemodellene på tall-linja. Svaret blir −10 i begge tilfeller, men representasjonen på tall-linja ser forskjellig ut.

Å betale seks kroner er altså det samme som å “få” minus seks kroner. Vi har regelen \(\overset{a - b}{\underset{a + -b}{↓}}\) (\(a\) har nå verdien -4 kroner, mens \(b\) har verdien 6 kr). Dette er samme regelen som over motsatt vei. Regelen gjelder altså begge veier. Vi skal skrive \(\overset{a + -b}{\underset{a - b}{⇵}}\) for å representere at regelen kan brukes to veier (dette er uvanlig syntaks). Vi skal senere introdusere tegnet = og syntaksen \(a + −b = a − b\) for å uttrykke at de to har lik verdi.

  • −8 − 3 blir .

  • −4 − 1 blir .

\(a - -b\)#

Dette er nok vanskeligste lov hittil: Vi skal subtrahere noen negativt. Dette er en av flere lover som går under navnet “minus og minus blir pluss”. Mange lærer nok dette som en instrumentell (Skemp, 1976) regel uten forståelse av hva som faktisk skjer. Vi

(Det er tre hovedgrupper med lover som blir kalt “minus og minus blir pluss”:

  • Subtraksjon (\(a − −b = a + b\)),

  • negativt tall (\(−−c = +c\)) (denne kommer vi tilbake til rett nedenfor)

  • multiplikasjon/divisjon (\(−d×−e = +de\) og \(\frac{-f}{-g} = +\frac{f}{g}\)) (denne kommer vi tilbake til når vi lærer om multiplikasjon og divisjon.)

Regnestykket $4 − −6” er krevende å representere eller eksemplifisere med fjerne-subtraksjon. Går det an å “få en bot på minus seks kroner”? Kanskje man kan si at temperaturen går ned seks grader per dag, og spørre hva den var i går; men dette blir fort krevende for elever.

Derimot kan man lett representere eller eksemplifisere det med differanse. Det er greit å se forskjellen på 4 og −6 på en tall-linje. Avstanden blir 10.

Vi ser at \(4 − −6\) er det samme som \(4 + 6\). Hvorfor er det slik? Vi kan iallfall skrive regelen \(\overset{a − -b}{\underset{a + b}{↓}}\), faktisk også motsatt vei \(\overset{a − -b}{\underset{a + b}{⇵}}\)

\(-a - -b\)#

Leseren oppfordres til å lage

  • en regnefortelling som illustrerer situasjonen

  • representasjon på tall-linja

  • −4 − −6 er . Hvordan regnet du ut dette; skrev du om til -4 + 6? Var du innom 6 − 4?

  • −3 − −7 er .

  • −8 − −6 er .

  • −54 − −56 er . Hvordan regnet du ut dette; forskjell-subtraksjon eller å trekke fra 50 på begge sider?

Tall alene#

\(-+a\)#

Vi har tidligere sagt at \(+5\) er det samme som \(5\). Disse kan vi også sette minustegn foran: Dermed blir \(-+5\) det samme som \(-5\).

\(+-a\)#

På samme måte er \(+-5\) det samme som \(-5\). Vi har altså at \(+-5\), \(-+5\) og \(+5\) det samme. Dette er en av lovene som blir kalt “pluss og minus blir minus” (en annen er \(-a × +b = -ab\)).

\(--a\)#

Hva med \(--5\)?

Nyttige ord her er “snu”, “motsatt” og “omvendt”. −5 er “5 snudd” eller “omvendt av 5”. Når vi snur noe to ganger kommer det tilbake. “Motsatt av motsatt” er “riktig-satt”. Noe som er “omvendt av omvendt” er som det var.

En huskeregel er at vi kan ta de to strekene (altså minustegnene), snu det ene, og sette oppå hverandre — da får vi tegnet “+”.

Vi kan også observere at på tall-linja må −−5 være like langt fra 0 som −5 er, men −−5 må være på motsatt side av 0 i forhold til −5. Dette stedet på tall-linja er +5.

Vi kan kanskje si at om 1 er , −1 er så blir −−1 det samme som som igjen er det samme som .

Vi har altså \(\overset{--a}{\underset{+a}{↓}}\). Dette er altså en av lovene som bærer navnet “minus og minus er pluss”. Det likner på loven \(\overset{b - -a}{\underset{b + a}{↓}}\); mange elever kan tenke at det er snakk om samme lov.

  • −17 er .

  • −−17 er .

  • −−−17 er .

  • −−−−17 er .