Påstander, utsagn

Forutsetninger og læringsmål

I kolonnerammeverket har vi påstander om objekt. Den vanligste typen påstander i skolen er likninger.

Introduksjon

Påstander (eller utsagn) er om matematiske objekt. Objekt er typisk av typen ℕ eller ℝ, mens påstander er sanne eller usanne (de er boolske; 𝔹?).

Generelle påstander

Noen påstander er konkrete (f.eks. 2 + 3 = 5). Noen er mer generelle (f.eks. \(x + 3 = 5\)). Generelle påstander har et generelt objekt (f.eks. en variabel) i seg.

Vi kan snakke om at en generell påstand er sann i noen situasjoner og usann i andre. Påstanden \(x² = 4\) er sann i to situasjoner — nemlig i den situasjonen at \(x\) har verdien 2 og at \(x\) har verdien −2.

En generell påstand kan altså tolkes som en angivelse av hvilke situasjoner påstanden er sann i.

Eksempler

• Konkrete påstander: 2 = 1 + 1, 2 < 3

• Generelle påstander: \(2 = x + 1\), \(x = 1\), \(x < 3\), \(x ≠ 4\)

Representasjoner

Ord

Vi har mange ord som betyr omtrent det samme: Påstand, utsagn. Mange typer påstander, for eksempel likninger, har en venstre- og en høyreside.

Vi vil bruke ordet situasjoner for instanser av påstanden TODO bedre definisjon.

Venn-diagram

Fig. 43 Venn-diagram eksempel: Og

I Venn-diagram er hvert område en situasjon.

Et Venn-diagram er nesten det samme som et Euler-diagram; men strengt tatt krever Venn-diagram at alle mulige områder er representert, mens Euler-diagram bare tar med de relevante.

Både Venndiagram og Eulerdiagram har navn etter personer; noen skriver dem med stor bokstav. Det heter iallfall ikke vennediagram, selv om dette høres koselig ut.

Sannhetsverditabell

I sannhetsverditabeller er hver linje én situasjon, med angivelse av verdier for variablene (f.eks. for A og B).

Table 9 Sannhetsverditabell

A	B	¬A	A ∧ B	A ∨ B
Sann	Sann	usann	Sann	Sann
Sann	usann	usann	usann	Sann
usann	Sann	Sann	usann	Sann
usann	usann	Sann	usann	usann

Av en eller annen grunn sier mange “Sannhetsverditabell” på norsk, selv om det heter bare “Truth table” på engelsk.

Python

I Python har man datatypen Boolean med verdier som True og False. Uttrykkene 4 > 3 og 3 == 3 er sanne.

Scratch

Fig. 44 Scratch Og

Fig. 45 Scratch Større enn

Fig. 46 Scratch Ikke

I Scratch har sannhetsverdier form som en sekskant, med spisser mot høyre og venstre. Dette i motsetning til tallverdier, som er avrundet mot høyre og venstre.

Vektstang

Vi tar med noen representasjoner som ofte blir brukt for å representere en spesiell type påstander: likninger.

Fig. 47 Skålvekt fra House of Math, med formelspråk inni

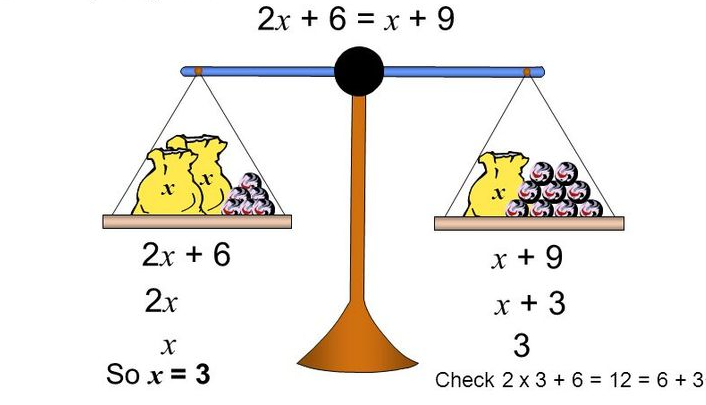
Fig. 48 Skålvekt fra the-world-is-my-classroom.weebly.com, med grafiske representasjoner inni

En vektstang er da “sann” om sidene er balanserte.

En vektstang vil ha inne i seg representasjoner av de to sidene. Disse kan være i formelspråket (som \(x + 3\) og \(5\)) i figuren, eller selv være grafiske.

Kurver

En likning kan også representeres som kurver. TODO

Formelspråket, likninger

I formelspråket representerer vi en likning som to sider med tegnet = mellom. Andre tegn (som < og ≠) gir andre typer påstander.

Dette kan vi vise tydelig ved bokser. Den ytterste boksen er en påstand; de indre er matematiske objekter kalt venstre- og høyresiden:
\(\fbox{\(\fbox{2 + \(x\)}\) = \(\fbox{\(x^3\) - 4}\)}\)

Det er selvfølgelig kjempeviktig at elever klarer å lese et uttrykk som \(2 + x = x^3 - 4\), og forstå at = “deler mer” enn + og −. Om noen skulle tenke at det betyr \(2 + \fbox{\(x = x^3\)} - 4\) har vi store problemer. En lærer kan understreke tolkningen ved å sette mer luft rundt likhetstegnet enn rundt de andre tegnene.

Aspekt

• Påstand (utsagn) som er sann eller usann

• Mengden påstanden er sann om (for generelle påstander). Eksempel “stjerna er rød” er uttrykk for alle røde stjerner. “Stjerne er rød” kan også brukes som en spesifisering/definisjon av stjerne. \(3 - x = 1\) kan være en definisjon for en mengde verdier for \(x\) (altså \({2}\)).

Læring

Det er vanlig at elever (og studenter!) blander objekter (f.eks. bokstavuttrykk) med påstander (f.eks. likninger). Representasjonene og reglene for bokstavuttrykk er noen andre enn dem for likninger!

Men…

Men… om objekt er det vi snakker om, kan ikke da påstander også gå inn i rollen som objekt? Kan vi da ha påstander om påstander? TODO To discussion