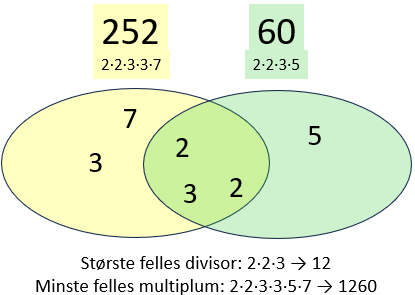
Minste felles multiplum#
A og B kommer på besøk hver 6. og hver 10. dag. Hvor lang tid blir det før de kommer sammen?
Vi kan tegne dette på tall-linje. For enkelthets skyld velger vi å tegne 6 og 10: TODO.
Først kan vi legge merke til at de kommer på besøk sammen dag 6×10, altså dag 60. Dette er et multiplum; men ikke det minste mulige.
Det minste felles multiplum finner vi ved å multiplisere alle primtallsfaktorene, men de som er felles multipliserer vi bare én gang. Vi multipliserer altså de som bare hører til 6 (3) med de som er felles (2) og de som bare hører til 10 (5) og får 30. Vi har nå spart en toer, og får derfor en verdi som er halvparten av vårt naive.
I mange sammenhenger når vi kan finne minste felles multiplum holder det også å finne hvilket som helst multiplum, for eksempel å multiplisere tallene. Det gjelder for eksempel ofte når vi senere skal forkorte brøker. Skal vi finne felles nevner for \(\frac{1}{6}\) og \(\frac{1}{10}\) er den minst mulige \(\frac{ }{30}\), men vi kan også bruke \(\frac{ }{60}\).
Noen vil assosiere dette med unionen av primtallsfaktorene.
Det er kanskje forvirrende at største felles faktor er et lite tall, mens minste felles multiplum er et stort tall.
“Minste felles multiplum” har også funnet sin vei inn i språket. Det betegner det man kan bli enige om. Ironisk nok ville det kanskje vært mer passende å kalle dette “største felles faktor”. “Minste felles multiplum” kan være et kompromiss; noen oppfatter uttrykket negativt ladet, andre positivt.
Forutsetninger og læringsmål#
Introduksjon#
Representasjoner#
Ord#
Stokk#
Unøyaktig formulering: Hva er den minste lengden før to stokker (f.eks. med lengde 3 og 4) “treffer” hverandre?
Vi ser at det er flere faktorer: 12, 24, 36… Men 12 er den minste av de felles faktorene.