× Multiplisere brøker#
Forutsetninger og læringsmål#
Multiplikasjon av brøker er mye enklere! Iallfall er formelen enklere.
Læringsmål#
Du skal kunne multiplisere to brøker.
Oppgaver#
(Martinussen, Smestad, 2010) i Tangenten Multiplikasjon og divisjon av brøk
Ndla, multiplikasjon og divisjon av brøk (se ned på siden for oppgaver)
Introduksjon#
Algoritmer#
Grafisk#
La oss si vi skal regne ut ⅔ × ⅕. Da skal vi først multiplisere nevnerne  og
og
 . Det har vi faktisk gjort før: Regnestykket blir
. Det har vi faktisk gjort før: Regnestykket blir 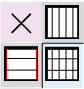 og resultatet
og resultatet  (altså \(\frac{}{3·5}\)).
(altså \(\frac{}{3·5}\)).
Så skal vi multiplisere tellerne 2×1  som blir 2.
som blir 2.
Det gir faktisk mening å sette dette inn i samme representasjon:  . Teller vi i kvotient-området (svar-området nederst til høyre), får vi at to av femten ruter har farve. Svaret er altså \(\frac{2}{15}\).
. Teller vi i kvotient-området (svar-området nederst til høyre), får vi at to av femten ruter har farve. Svaret er altså \(\frac{2}{15}\).
Med formel#
Vi har nå vist multiplikasjon i flis-språket. Med ord kan vi si at vi multipliserer tellerne for seg og nevnerne for seg. Med formel kan vi si \(\overset{\frac{a}{b}·\frac{c}{d}}{\underset{\frac{a·c}{b·d}}{↓}}\). Vi må multiplisere tellerne og nevnerne hver for seg.
\(n×\frac{a}{b}\)#
Har vi et heltall (f.eks. 2) og en brøk (f.eks. ¾), kan vi gange dem ved å gange heltallet inn i nevneren: \(\frac{2×3}{4}\). I dette tilfellet blir svaret \(\frac{6}{4}\), som kan forkortes til \(\frac{3}{2}\).
Dette ser vi kanskje enklest ved å bruke repetert addisjon: 2×¾ er ¾+¾, altså  +
+  . Vi ser at vi får seks firedeler, altså
. Vi ser at vi får seks firedeler, altså  . I dette tilfeller (og alle tilfeller hvor n har felles faktor med nevneren b) må vi samle (her til
. I dette tilfeller (og alle tilfeller hvor n har felles faktor med nevneren b) må vi samle (her til  ).
).
Vi har at \(\overset{n×\frac{a}{b}}{\underset{\frac{n×a}{b}}{⇵}}\).
Didaktikk#
Multiplikasjon kan gi noe mindre!#
Elever som bare har ganget med heltall, er kanskje vant til at a·b må være større enn a. Dette gjelder jo om b > 1; og om b er en blir jo resultatet noe som er likt a. Men om b er en brøk (eller noe annet som er mindre enn a) blir jo produktet a·b mindre enn a.
