Den assosiative lov

Forutsetninger og læringsmål

Introduksjon

Den assosiative lov er en egenskap ved noen operatorer. Om en operator ⊕ er assosiativ stemmer regelen \(\overset{a ⊕ (b ⊕ c)}{\underset{(a ⊕ b) ⊕ c}{↓}}\). For eksempel er + assosiativ fordi regelen \(\overset{(a + b) + c}{\underset{a + (b + c)}{↓}}\) er sann.

Representasjoner

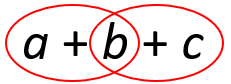
Fig. 18 Assosiativitet

Navn

Dette er forskjellige måter å si det samme på:

• ⊕ er assosiativ

• ⊕ tilfredsstiller den assosiative lov

• Den assosiative loven er sann for ⊕

• Det er altså likegyldig om vi sier \(a ⊕ (b ⊕ c)\) eller \((a ⊕ b) ⊕ c\).

Ordforklaring: Assosiativ

Fra “ad” og “sammen”. Sammenlikn society og sosial. Fra ad- og proto-indoeuropeisk *sokʷ(h₂)-yo- (følger, kompanjong).

Ord

Med ord kan man si at en operator er assosiativ om det er likegyldig hvilke av argumentene som hører tettest sammen.

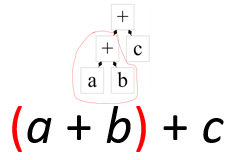
Fig. 19 Assosiert til venstre

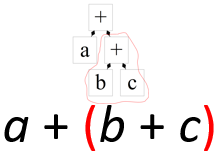
Fig. 20 Assosiert til høyre

Formelspråk

Den assosiative lov for ⊕ er altså \(\overset{a ⊕ (b ⊕ c)}{\underset{(a ⊕ b) ⊕ c}{⇵}}\), ofte skrevet \(a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c\).

Vi kan også si dette prefiks: \(⊕(a, ⊕(b, c)) = ⊕(⊕(a, b), c)\).

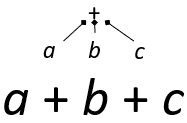
Fig. 21 Siden + er assosiativ kan vi velge hvordan vi tolker \(a + b + c\) og droppe parentesene.

Siden begge tolkinger gir samme verdi kan vi droppe parentesene

For operatorer som er assosiative har det altså ikke noe å si hvordan vi tolker parentesene. Dermed kan vi droppe dem. Vi sier rett og slett \(a ⊕ b ⊕ c\) uten å velge om det betyr \(a ⊕ (b ⊕ c)\) eller \((a ⊕ b) ⊕ c\). For eksempel sier vi 2 + 3 + 4 uten parenteser.

Syntakstre og bokser

TODO

Algoritmer

Å sjekke om en operator er assosiativ

Skal vi sjekke om en operator er kommutativ kan sette inn operatoren i den assosiative lov (\(⊕ ↦ ×\), om man vil) og sjekke om det stemmer. Om vi for eksempel skal sjekke om multiplikasjon er assosiativ kan vi sjekke om det stemmer at \((a × b) × c = a × (b × c)\). Om dette stemmer er × kommutativ.

Er divisjon kommutativ?

Vi har fortsatt våre vanlige teknikker:

• Bevise formelt med utregninger basert på eksisterene regler

• Gjøre handling i en representasjon

• Eksempel, som kan lage intuisjon, bli et generisk eksempel eller moteksempel.

Operatoren “er lik” er ? kommutativ ikke kommutativ .

Flere eksempler og oppgaver

Oppsummering (noen av disse er tatt før):

• Addisjon er ? assosiativ ikke assosiativ .

Løsningskommentar

Addisjon: Handling i representasjonsspråk/generisk eksempel i småstein eller tall-linje?

• Subtraksjon er ? assosiativ ikke assosiativ .

Løsningskommentar

\((a - b) - c\) ? er lik er ikke lik \(a - (b- c)\). Det ser vi for eksempel ved å sette inn 5, 3 og 1 for de tre variablene. \((5 - 3) - 1\) er mens \(5 - (3 - 1)\) er .

• Multiplikasjon er ? assosiativ ikke assosiativ .

Løsningskommentar

Litt tricky kanskje; se assosiativitet under multiplikasjon. Man kan også lage generisk eksempel på representasjonene av gjentatt multiplikasjon under potens.

• Divisjon er ? assosiativ ikke assosiativ .

Løsningskommentar

Vises ved moteksempel.

• Potens er ? assosiativ ikke assosiativ .

Løsningskommentar

Vises ved moteksempel.

Aspekter

Talltyper

Læring

Mulig aktivitet: Drama i praksis: Hvem vil jeg være sosial med?

Venstre- og høyreassosiativitet.

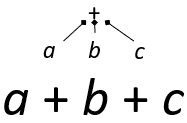
Fig. 22 Assosiativitet

Hva med minus? Hvordan skal vi tolke 2 - 3 - 4? Vår kultur har bestemt seg for å tolke dette som (2 − 3) − 4. Vi tolker det altså venstre-assosiativt.

Dette er en egenskap ved formelspråket og ikke matematikken. Vi velger å tillate oss å skrive \(a ⊕ b ⊕ c\) uten parenteser; det er det samme om folk tolker det som \(a ⊕ (b ⊕ c)\) eller \((a ⊕ b) ⊕ c\).

Skriv uttrykket 2^3^4 inn i Excel, Google og Wolfram Alpha, og sammenlikn svarene. Forklaring under potens. Wolfram Alpha kan dere godt kjenne til.