Ny = gammel + økning#
Forutsetninger og læringsmål#
Introduksjon#
Ny = gammel + økning#
Dette kan synes som en svært enkel formel. Likevel skal vi legge merke til noen utfordringer.
“Look here, George”, said his cousin Reginald. “By what fractional part does four-fourth exceed three-fourth?” “By one-fourth!” shouted everybody at once. “Try another one,” George suggested. “With pleasure, when you have answered that one correctly” was Reginald’s reply. Fra [Mason et al., 2010] “Fractious, p.31”
Representasjoner#
Grafisk #
Det er fortsatt viktig å være tydelig på hva som er helheten. Det kan vi tegne med en svart ramme:
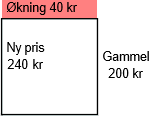
Ord#
Gammel er ofte det samme som helhet i formelen \(andel = \frac{del}{helhet}\).
Økning er noen ganger det samme som del. Om økningen er negativ, brukes ofte ord som rabatt.
Ny kalles også “etter” eller liknende. Denne har samme enhet (for eksempel “kroner”) som gammel. Om økningen er positiv er denne større enn den gamle.
Oppgaver
Om gammel pris er 200 kr og rabatten er 50 kroner, er “økningen” . Ny pris er kr.
Om et beløp øker med 200% er det blitt
Om et beløp øker med 100% er det blitt
Sammenheng med andel = del/helhet#
Ofte har vi oppgitt økningen prosentvis. Da kan vi bruke formelen \(andel = \frac{del}{helhet}\), men andel er nå det samme som prosentvis økning, helhet er gammel pris og del er det samme som prisøkning. Vi har altså \(prosentvis økning = \frac{prisøkning}{gammel pris}\) som gir \(prosentvis økning × gammel pris = prisøkning\).
Vi kan også si at ny pris = gammel pris + prosentvis økning × gammel pris.
Det er alltid et mål at elevene skal beholde sammenhengen med situasjonen, og tenke selv, heller enn å tenke i ferdige formler. TODO
TODO: Noen oppgaver om større beløp med rabatt hvor man skal finne ny pris
La oss fortsatt si at gammel pris er 200 kroner; men prosentvis økning er 30%. Da får vi at prisøkningen er kroner. Nå vet vi gammel pris og prisøkning. Det gir en ny pris på kroner.
Vekstfaktor#
Vi kan også si at ny pris = gammel pris + prosentvis økning×gammel pris = gammel pris×(1 + prosentvis økning).
Her opptrer faktoren 1 + prosentvis økning. Det er ofte praktisk å gi denne et eget navn; vi kaller den vekstfaktor.
Er prosentvis økning 30%, er altså vekstfaktoren .
Er prosentvis økning minus 20%, er vekstfaktoren .
Er økningen ½, er vekstfaktoren .
Er vekstfaktoren 1.1, er prosentvis vekst %.
Er vekstfaktoren 0.7, er prosentvis vekst %.
