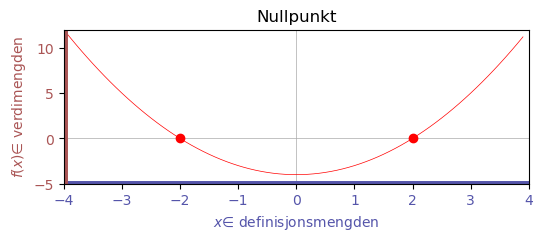
NullpunktIKKE FERDIG#
Representasjoner#
Ord#
Nullpunkt er punktene hvor funksjonsverdien er 0.
Noen ganger brukes ordet nullpunkt om de argumentene som gir verdien 0. Ellef mener nullpunkt best defineres som et punkt. Eksempel: Et nullpunkt er \((3, 0)\), ikke bare \(3\).
Formelspråk#
\(f(x) = 0\).
Algoritmer#
Sjekke et nullpunkt ved å regne ut#
Om man skal sjekke om \((3, 0)\) er et nullpunkt: Regne ut \(f(3)\) og sjekke at det blir 0.
Regne ut ved likning#
Om man skal finne nullpunktet til \(f(x)\): Løse likningen \(f(x) = 0\); om man får at \(x = 3\) er en løsning er \((3,0)\) et nullpunkt.
Bruke formel#
For noen funksjonstyper, for eksempel førstegrads- og andregradsfunksjoner, finnes det formler (egentlig for første- og andregradslikninger).
Digitale hjelpemidler#
F.eks. Wolfram Alpha eller ChatGPT kan løse likninger for deg. Om du ikke kan bruke dette på eksamen er det veldig nyttig i praksis.
Leite seg fram#
Særlig egnet om man vet at funksjonen går oppover (evt. nedover):
Prøve ut å regne ut verdier av \(f\); om \(f(x)\) blir mindre enn 0 øker man \(x\) litt og omvendt.
Variant: Newtons metode.