Rasjonale tall#
Introduksjon#
Hva om vi skal dele to fyrstikker i fire? Det kan være en interessant pedagogisk opplevelse å la barn fundere på en slik oppgave.
De fleste barn vil etter en tid komme fram til løsningen: Man må dele fyrstikkene i to. Barna har kanskje erfaring med begrepet “halv”.
Tallet “halv” er ikke en et heltall. Vi kaller det et rasjonalt tall. Rasjonale tall er resultatet av divisjonsstykker. Vi skal senere se at relle tall kan skrives som brøker.
Tidligere har vi bare snakket om heltall. Det finnes altså mange flere tall enn vi trodde!
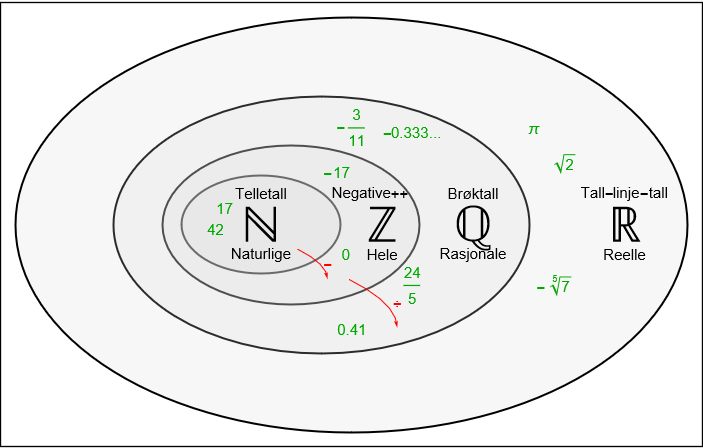
Alle naturlige tall er også heltall. Alle heltall er også rasjonale tall. Dette kommer fram i Venn-diagrammet til høyre.
De rasjonale tallene er “brøktallene”, tallene vi kan få ved å dividere to heltall.
Tidligere har vi bare snakket om ℕ og ℤ, revolusjonerende! Todo
Representasjoner#
Ord#
Talltypen kalles “rasjonale”, ikke fordi de er fornuftige, men fordi de oppstår som ratios.
Formelspråket#
ℚ. Huskeregel: quotient.
Brøker#
Desimaltall#
Rasjonale tall kan ofte representeres som desimaltall. Resultatet av 3÷2 er for eksempel 1.5.
Alle desimaltall kan framstilles som rasjonale TODO hvorfor
Det finnes riktignok rasjonale tall som ikke lar seg representere som desimaltall (i titall-systemet) (med endelig antall sifre). Resultatet av 1÷3 får uendelig antall desimaler: 0.33333….
Tall-linje#
1.5 er også enkel å framstille på tall-linja:

Steinbit#
Vi kan utvide småstein-representasjonen til å håndtere deler av steiner. Det er ofte praktisk å tegne svarte rammer for å framheve “helhetene”. 1.5 kan være  . Ofte er det praktisk å zoome litt inn:
. Ofte er det praktisk å zoome litt inn: 
Algoritmer#
Rasjonale tall kan adderes, subtraheres, multipliseres og divideres. Riktignok kan man ikke dele på 0 (one can’t share without anybody to share to). Det aller meste vi har sagt om representasjoner, både på tall-linja, i småsteinspråket og flisspråket, gjelder også for rasjonale tall. For nå nøyer vi oss med eksempelet 1.5×1.5: 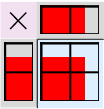
TODO seinere: Reelle#
Reelle tall#
Finnes tall som ikke er rasjonale (ikke kan skrives som brøk)? Nei, mente kanskje de som fant opp “rasjonale”; ordet betyr “fornuftige” og betyr vel at det er ufornuftig å tenke på andre. Nei, mente Pytagoras. Men en av Pytagoras’ disipler, Hippasus, beviste at √2 ikke kunne skrives som brøk. Da ble Pytagreerne i følge legenden så sure at de druknet ham. Det var allerede da farlig å fortelle sannheten. Beviset er på pensum i de fleste beviskurs (som MA302), men her er straffen motsatt: Om du ikke klarer å bevise at √2 ikke klarer å skrives som brøk risikerer du dårlig nattesøvn.
Alle tall på tall-linja kalles reelle. Noen av dem (faktisk de fleste) er altså ikke rasjonale. Eksempler er √2, og π. Mengden av de reelle tall kalles ℝ. Se videre Venn-diagrammet over.
Det meste man kan gjøre med rasjonale tall kan man også gjøre med reelle. Man kan for eksempel addere, subtrahere, multiplisere og dividere dem (unntatt ÷0). Lovene blir ganske like som for rasjonale tall, men de er forbausende vanskelige å bevise formelt. Reelle tall er forbausende vanskelig å definere formelt; dette ble først gjort av Richard Dedekind rundt 1872.
