Ganging#

Forutsetninger og læringsmål#

Vi skal nå introdusere multiplikasjon. Vi vil utnytte småstein-representasjonen, særlig av addisjon.

Graph

Vi skal gå gjennom repetert addisjon til flisrepresentasjonen . Denne skal vi også bruke på andre talltyper.

Introduksjon: Steiner i farger#

Vi har to steiner i hver av fargene rød, blå og grønn. Hvor mange steiner har vi tilsammen?

Repetert addisjon#

Vi kan selvsagt representere dette med farger på steinene: . I småsteinrepresentasjonen er det lett å se at dette er lik .

Hver farge er en gruppe. Vi kan også markere gruppene på en annen måte:

Her er addert ganger. Å addere det samme flere ganger kalles *repetert addisjon”. Repetert addisjon kan også representeres på tall-linje:
Også her ser vi tydelig antall grupper, størrelsen på hver gruppe og svaret.

Med ord kunne vi si at vi tar “tre ganger addisjon med to”, “tre ganger grupper på to” eller “tre ganger to”.

Stabling#

Vi skal nå stable steinene oppå hverandre. Da får vi . Uten farger blir det

Antall rader (etasjer) blir antall grupper (farger) (i vårt eksempel: ).
Antall kolonner (antall i her etasje) blir antall ere i hver farge (i vårt eksempel: ).
Vi kan tydeliggjøre dette dette i tegningen, ved å legge til til venstre og øverst: 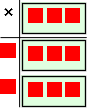. Siden vår kultur leser fra venstre og ovenfra velger vi å sette dem til venstre og over for .

er like mange som .

  • stablet ganger blir .

Representasjoner#

Ord#

Regnestykket skal vi kalle “tre ganger to”. Vi kan også si “å gange tre og to”.

Ordforklaring: Multiplisere

Vi skal også bruke ordet multiplikasjon. Det latinske ordet “multi” betyr “mange”, og “plisere” betyr “brette” eller “stable”.

For språknerder: Noen vil replisere at også applisere er en duplisering av -plisere. Det vil implisere at alle disse abstrakte ordene har å gjøre med bretting. Det ekspliserer at mange begrep vi til daglig oppfatter som abstrakte blir representert av konkrete representasjonsspråk. Det kan vi med fordel eksplisere ved å applisere konkrete representasjoner i våre eksplikasjoner.

Resultatet av en multiplikasjon (her: 6) kalles produkt. Operandene (det som blir multiplisert) (her: 3 og 2) kalles faktorer. Vi har altså at faktor ganger faktor blir produkt.

Ordforklaring: Faktor

På latin betyr vel “faktor” noe sånt som “det som skaper” og “produkt” “det som er fram-ledet”. En huskeregel kan være en engelsk fabrikk (factory) som produserer noe.

Formelspråket#

I formelspråkene bruker vi symbolene × eller ·. Vi skriver dem vanligvis mellom operandene (mellom det som skal multipliseres): 3×2 eller 3·2.

Vi har altså definisjons-regelen \(\overset{a × b}{\underset{b+b+b…\ a\ ganger}{↓}}\)

Symbolene × og · betyr nøyaktig det samme (iallfall så lenge vi snakker om tall). Det finnes historiske årsaker til at noen land foretrekker det ene; det finnes også praktiske argumenter for å bruke det ene eller andre; × kan forveksles med bokstaven x, mens · kan bli litt usynlig i håndskrift. Noen lærere veksler for å gjøre elevene vant til begge varianter og for å være tydelige.

I visse praktiske situasjoner brukes tegnet * (asterisk) fordi det likner på × og er lett tilgjengelig på vanlige tastatur. Det er akseptabelt når det er viktig å skrive fort, men ikke når man skal vise kvalitet eller respekt for sine lesere.

Senere, når vi kommer til variable, skal vi også se at vi i visse sammehenger kan kutte ut gangetegn: 3x betyr 3·x mens ab betyr a×b. Denne skrivemåten kalles implisitt multiplikasjon.

Småstein og fliser#

[Klaveness, Karlsen, and Kverndokken, 2019] 83s324

https://phet.colorado.edu/en/simulations/area-model-multiplication

Vi skal nå utvide småstein-representasjonen til flis-representasjoner. Slike representasjoner blir også kalt areal-representasjoner, men vi velger å kalle dem fliser fordi de på engelsk blir kalt for tiles. Dette er altså snakk om firkantede fliser som dem du har på badet. I dette dokumentet vil de oftest ha fargen .

Flisrepresentasjonen er slik:

  • Til venstre setter vi en representasjon av første faktor. Denne er det praktisk å ha loddrett.

  • Øverst setter vi en representasjon av andre faktor.

  • Området til høyre og under faktorene representerer produktet. Dette får ofte bakgrunnsfargen .

Utifra denne definisjonen kan altså 2×4 representeres som .
Vi kan telle opp at produktet blir det samme som . Husk hele tida at om det er vanskelig å forstå hva 2×4 betyr, kan vi alltid “stable ned” til +.

Hver flis er produktet av flisen helt til venstre og flisen høyst over#

For hver lille flis i produkt-området kan vi multiplisere det som er på samme rad i faktoren til venstre med det som er i samme kolonne i faktoren over. Hittil har vi bare sett at til venstre og øverst blir . Vi kan skrive , det vil si at 1×1 er 1, eller at én ener blir én.

Dette fungerer også om det står , som er det samme som , til venstre: 12×4 blir
, som blir .
Dette kan begrunnes mer detaljert ved å tegne opp at 12×4 er definert med tolv grupper av , og 10×4 er ti grupper av stablet. Dette kan også skrives med bare enere lage bilde.

Det fungerer også om det står øverst: 2×14 blir , som blir . Dette kan også begrunnes med mer detaljer, ved å se bl.a. at 2×10 er to tiere stablet.

100 i småstein- og flis-språkene#

Hva er 12×14? Her har vi både til venstre og øverst — altså i både første og andre faktor.

Faktorene kan settes opp som . De fleste flisene i produkt-området kan settes opp greit, men en ny utfordring er 10×10: . Rent geometrisk ser det ut til å bli . Symbolet har vi ikke sett før, men det er en naturlig utvidelse av småstein- og flis-språkene. Vi definerer altså til å representere 100.

Dermed kan vi representere 12×14 som
.
Vi kan finne svaret med å telle antall re, antall ere (inkludert antall ere) og antall ere i produktet. Svaret blir ; vi skal se på flere detaljer nedenfor under algoritmer.

Sette opp med enere først - lage bilde

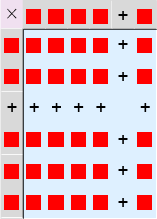
Flisrepresentasjon av produkt av sum#

Vi tar allerede nå med representasjon av f.eks. (2 + 3) × (4 + 1), altså produkt av to summer. Reglene vi har formulert hittil er formulert så dette går an. Vi tar første faktor (altså 2 + 3) i venstre kolonne og andre (4 + 1) i øvre, og multipliserer hver flis. Det kan representeres som

Flisrepresentasjonen av produkt av variable#

Reglene vi har definert fortsatt gjelder også om variable. Vi skal utvikle naturlige representasjoner når vi jobber med regneregler nedenfor.

Men la oss for eksempel representere (2+10)×(1+x):

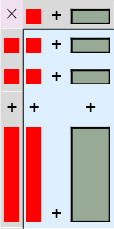
Mer om formelspråket: Presedens (ikke regnerekkefølge)#

Hva er resultatet av 2+3×4? Vi har to muligheter:

  • Om vi først adderer 2 + 3 (og får ) og multipliserer med 4 får vi . Denne forståelsen kan representeres med \(\fbox{\(\fbox{2 + 3}\) × 4}\)

  • Om vi først multipliserer 3 x 4 (og får og så adderer med 2 får vi . Denne forståelsen kan representeres med \(\fbox{2 + \(\fbox{3 × 4}\)}\)

Hva er rett?

Vi kan legge merke til at spørsmålet ikke handler om matematikk. Spørsmålet handler ikke egentlig om addisjon eller multiplikasjon. Spørsmålet handler om hvordan disse blir representert i formelspråket. Formelspråket er et språk vår kultur har valgt og definert. Naturen og universet sier altså ikke hva som er rett. Men vår kultur har en mening. Vår kultur kunne valgt annerledes.

Svaret i vår kultur er at den siste muligheten er riktig — svaret er 14. Multiplikasjon hopper inn i bokser før addisjon. Litt mer teknisk kan vi si at × binder sterkere enn +, eller at × har høyere presedens enn +.

I mange tilfeller regner vi ut slike bokser innenfra:
\(\begin{array}{r c} & \fbox{2 + \(\fbox{3 × 4}\)}\\\hdashline \textrm{blir til}&\fbox{2 + 12} \\\hdashline \textrm{som blir til} &\fbox{14} \end{array}\)
I disse enkle tilfellene får vi da at “ganging alltid gjøres før pluss”. Denne regelen gjelder i de fleste tilfeller innenfor aritmetikk uten parenteser (altså lavere deler av barneskolen). Derfor er det noen matematikklærere som bruker ordet regnerekkefølge om dette fenomenet. Det er uheldig, for ordet kan få elever til å tro at dette egentlig handler om rekkefølge av regning, altså om matematikk. Fenomenet handler ikke om regning, men om tolkning. Muligens ville et bedre ord vært tolkningsrekkefølge. Vi snakker iallfall om hvordan vi tolker et uttrykk i formelspråket. Disse tingene oppstår ikke i småsteinspråket eller andre språk. Det er heller ikke alltid vi regner boksene innenfra; et eksempel er 2×a + −2×a, som er umulig å regne ut med “regnerekkefølge”. Eksempelet 2×31415 - 2×31415 er vanskelig å regne ut med lik “regnerekkefølge”.

Elevene får dypere forståelse om de lærer om en eller annen form for bokser (eller syntakstrær).

Senere skal vi se at vi i vanlig formelspråk kan uttrykke slike bokser med parenteser. Om vi virkelig ønsker å uttrykke \(\fbox{\(\fbox{2 + 3}\) × 4}\) kan vi bruke parenteser til å uttrykke boks: \((2 + 3) × 4\). Vi kan tenke på parentesene som en boks.

Dette er også viktig forståelse i programmering.

Til inspirasjon for nerder, særlig språk- og programmeringsnerder: Dette kan også representeres som syntakstrær, for eksempel

Graph

Algoritmer#

Repetert addisjon#

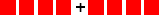Noen ganger er det naturlig å regne ut verdien av et multiplikasjonsuttrykk rett og slett ved å bruke repetert addisjon: kan skrives som , altså . Dette er mulig når første faktor er et naturlig tall; kanskje bare praktisk når det er et lite, naturlig tall. Vi kan også sette det opp som en utregning:

eller på en annen måte:

Graph

Dette fungerer også om det er tiere involvert: Tre ganger tolv kan tolkes som , altså som blir . Utregningen kan settes opp som
.

Én ganger A blir A: \(\overset{1×a}{\underset{a}{↓}}\): kan “stables ned” til bare .

Vi kan legge merke til at vi bruker en del “inni-algoritmer”, særlig addisjonsalgoritmer, når vi gjør en multiplikasjon.

Telle i produktområdet#

Som sagt kan vi representere f.eks. 12×13 i flismetaforen og så telle opp i produktområdet.

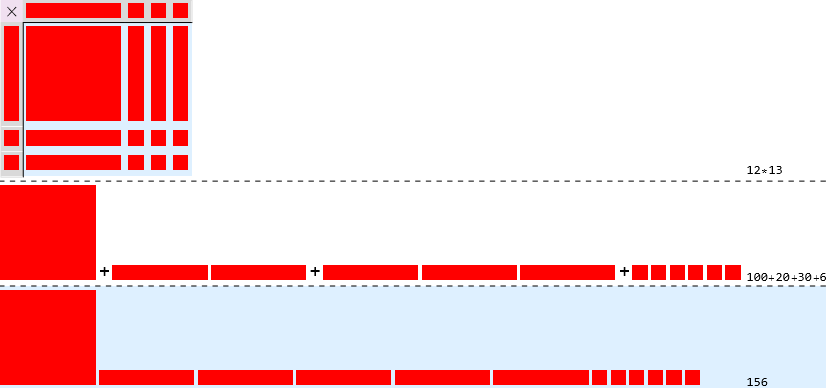
Vi skal nå studere litt mer detaljert. Vi kan sette opp produktområdet med farger
hvor altså representerer 100, 20, 30 og representerer 6. Da kan utregningen representeres med (kanskje litt mange) detaljer som

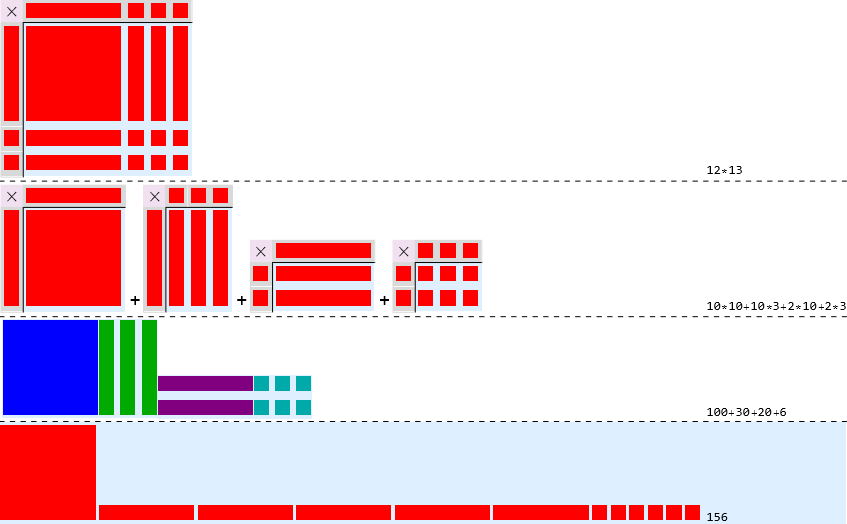
Vi kan komme til å få mer enn 10 ere. Det skjer for eksempel i regnestykket 14×13, som blir . Det behandles med veksling på vanlig måte.

Her har vi tegnet opp både flisrepresentasjoner (til venstre) og formler (til høyre). Ofte tenker man bare i fliser (i hodet) eller skriver ned bare formler (på papir).

  • 11 × 11 er (her kan du gjerne tegne opp på et ark de første gangene)

  • 12 × 14 er (det kan også være en hjelp å skrive opp mellomregning: 100 + 20 + 40 + 8)

  • 13 × 14 er

  • 21 × 13 er

Forbindelsesstreker (alle med alle) #

En huskeregel, særlig ved hoderegning, er å sette opp streker mellom hvert par av sifre:

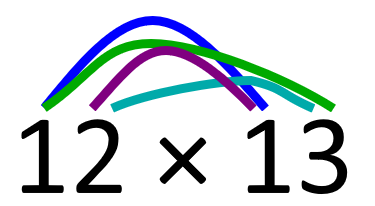
Fargene i strekene samsvarer med fargene i tegningen over; for eksempel representerer den blå streken 10×10, som blir 100.

  • 21 × 23 er

  • 21 × 34 er

Rutenett-oppsett#

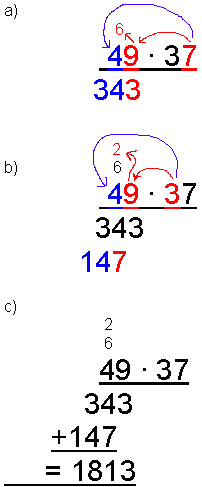
../../_images/multiplicationTraditional.png

Fig. 1 Tradisjonell rutenettsalgoritme fra matematikk.net#

Et mulig oppsett, som synliggjør både multiplikasjon og addisjon, er
. Denne er rask å skrive, men kanskje litt vanskelig å forstå. I gamle dager var det også et poeng at den sparte papir og blekk; i våre dager er det siste sjelden en begrensning, særlig på datamaskin.

Det eksisterer en forkortet av denne som i gamle dager var så vanlig at den ble kalt “standardalgoritmen”. Den hadde den fordelen at den var enda raskere å skrive og sparte papir og blekk; men den var vanskeligere å forstå, førte til flere feil og tok for de fleste lang tid å bruke. Den hadde altså fordeler historisk, men har fordeler for oss. Interesserte kan søke på Internett etter “standardalgoritmen for multiplikasjon”. Det finnes fortsatt studenter som har lært denne på skolen.

Regneregler#

Selv om vi ikke har definert variable enda, vil vi noen steder lage regler med bokstaven a. For a kan du sette inn hvilket som helst tall, for eksempel 3. Lover med a er altså generelle: De gjelder for alle tall.

0a#

Ingen ganger hvasomhelst blir ingen. For eksempel har vi . Generelt har vi \(\overset{0 × a}{\underset{0}{↓}}\). Vi har også, ved kommutativ lov, \(\overset{a × 0}{\underset{0}{↓}}\) (mange ingen-er blir ingen).

1a#

Én av noe blir “noe”. For eksempel har vi . Generelt har vi (altså \(\overset{1 × a}{\underset{a}{↓}}\)).
Vi har også, ved kommutativitet, (\(\overset{a × 1}{\underset{a}{↓}}\)).

2a (dobling)#

To av noe blir “noe pluss noe”. For eksempel blir like mange som . Generelt har vi at er lik , altså \(\overset{2 × a}{\underset{a+a}{↓}}\).

10a#

Ti ganger noe er i titall-systemet å flytte komma én plass (vi har riktignok ikke definert komma ennå), eller å legge til en 0. 10×31 = mens 10×12.81 = .

Vi trenger en ny representasjon for 10a. Den følger naturlig i flisrepresentasjonen: .

−1a#

At a ganger −1 er −a er greit å forstå ved repetert addisjon

Minus en ganger noe er “minus noe”. \(\overset{-1 × a}{\underset{-a}{⇵}}\).

Automatisering#

Det finnes en del generelle regler som er enklere å huske enn enkelt-regnestykker. Vi har \(\overset{0 × a}{\underset{0}{↓}}\), \(\overset{1 × a}{\underset{a}{↓}}\) og \(\overset{2 × a}{\underset{a+a}{↓}}\), og andre lover som blir behandlet nedenfor.

Automatisering av gangestykker#

Vi kan regne ut for eksempel 4×5 på disse måtene.

Når en elev har regnet ut 4×5 en del ganger, vil hun kanskje huske regelen \(\overset{4×5}{\underset{20}{↓}}\) automatisk. Når hun så møter 4×5, vil hun finne regelen i sitt regel-bibliotek og bruke den uten å regne manuelt.

Det som begynte som en algoritme og et bevis, har altså blitt en regel. Men om det trengs, kan vi gå inn i regelen og tolke den som repetert addisjon eller flisutregning.

Det er praktisk å ha en del slike regler. Vi kan også bygge opp biblioteket bevisst, ved å pugge gangetabellen.

Gangetabellen ble i gamle dager lært ved å pugge først og forstå etterpå. Dette er … umoderne pedagogikk. Læreplanen snakker om å eksperimentere, representere og utforske multiplikasjon, men ikke å pugge. Likevel vil mange mene at gangetabellen er en av stedene hvor pugging faktisk fungerer.

De finnes 100 mulige multiplikasjonsstykker i den lille gangetabellen (hvor hver multiplikand er fra 1 til 10). 1×n og 10×n, og de motsatte er trivielle; 2×n er dobling og 5×n halvering (og tidobling). Mange av stykkene er symmetriske (kommutative); dermed står vi egentlig bare igjen med 21 stykker som må pugges.

Matematikk.org har en gangetester/gangetrener.

Kommutativ lov#

For addisjon var den kommutative loven \(\overset{a + b}{\underset{b + a}{⇵}}\). Denne er mer eller mindre selvsagt i småsteinspråket.

Stemmer den kommutative lov for multiplikasjon — altså \(\overset{a × b}{\underset{b × a}{⇵}}\)? Om vi prøver ut en del eksempler (f.eks. 2 × 3 og 3 × 2) ser vi at loven stemmer. Men eksempler er ikke bevis.

Om vi setter opp 2×3 som repetert addisjon får vi .
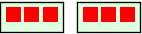Dette kan vi stable til eller . I utgangspunktet hadde vi to grupper à tre ere, , men vi kan også velge å se på kolonnene som grupper; da får vi tre grupper à to ere, 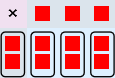. To treere er altså det samme som tre toere. Sånn må det være for alle tall.

Dette er i utgangspunktet ikke en selvfølge for et barn (det tilsvarende stemmer ikke for subtraksjon!) Likevel vil barn etterhvert bli så vant til dette at det framstår som en selvfølge.

Blant voksne representeres loven med munnhellet “faktorenes orden er likegyldig”, som brukes både om multiplikasjon og andre “faktorer” som kan komme i vilkårlig rekkefølge.

Vi kan også snakke om den kommutative lov mer generelt.

Assosiativ lov#

For addisjon var den assosiative loven \(\overset{a + (b + c)}{\underset{(a + b) + c}{⇵}}\).

Stemmer en tilsvarende assosiativ lov for multiplikasjon — altså \(\overset{a × (b × c)}{\underset{(a × b) × c}{⇵}}\)?

Det stemmer for eksemplene vi kan finne på.

Vi kan også lage regnefortellinger som kan overbevise oss om at dette alltid må stemme. I forsvaret i et land har hvert kompani fire tropper, hver tropp har tre grupper og hver gruppe har fire personer; antallet personer per kompani er det samme om man først regner antall personer per tropp eller om vi først regner antall grupper per kompani.

Noe tilsvarende kan vi også representere med repetert addisjon. 3×4 blir tre grupper med fire:
2x(3×4) blir to av det samme:

2×3 blir to grupper med tre:
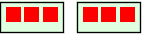(2×3)×4 blir det samme ganger . Setter vi inn får vi

Dette er mye vanskeligere å illustrere ved flisrepresentasjonen, som har vanskelig med gjentatt multiplikasjon.

Vi kan også snakke om den assosiative lov mer generelt.

Distributiv lov#

Vi skal nå introdusere en tredje lov; den berører ikke bare én operator (multiplikasjon), men to (multiplikasjon og multiplikasjon) på en gang.

For å skape intuisjon begynner vi med et eksempel: To barn skal hver få tre epler pluss fire pærer . Det er det samme som at to barn skal få tre epler pluss at to barn skal få fire pærer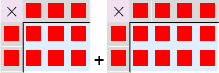

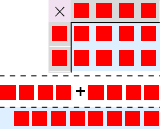
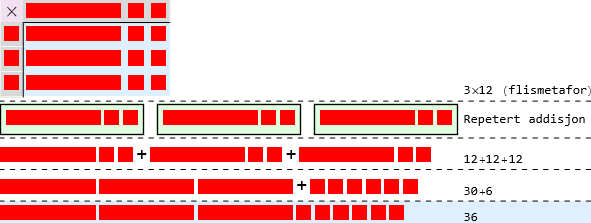
Et annet eksempel er 3×12 . Vi har jo at er det samme som . Vi har altså at (3×12) er lik (3×10 + 3×2)

Vi har at \(\overset{a × (b + c)}{\underset{a×b + a×c}{↓}}\). Dette kalles at multiplikasjon distribuerer over addisjon.

Igjen har vi en algoritme som først er et bevis og så blir en regel vi kan legge til i regelbiblioteket vårt og bruke i andre sammenhenger.

Det er at multiplikasjon også distribuerer over subtraksjon.

Talltyper#

Mulige faktorer#

Om vi tenker i repetert addisjon må første faktor være et [naturlig tall](natural]. Det er vanskelig å tegne opp −2 ganger noe eller a ganger noe i repetert addisjon.

Om vi tenker i flismetaforen, derimot, kan både første og andre faktor være negative tall. Se disse eksemplene, som vi foreløpig stiller opp uten begrunnelse:

  • −2×3 er

  • 3×−4 er

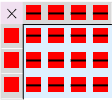
  • 2×a er Vi skal senere se at flismetaforen håndterer også andre talltyper, blant annet brøk og desimaltall.

Vi kan multiplisere også andre ting: Hver togvogn har en konduktør, tre barn og ti voksne. Vi har tre vogner. Hvor mange er i vognen? Her kan vi bruke algoritmen “repetert addisjon” (altså bare addere alle menneskene bortover skinnene) eller “flisrepresentasjon” (stable vognene oppå hverandre).

  • −13×2 er Kan regnes ut på forskjellig måte, f.eks. med kommutativ lov og repetert addisjon: 13 + 13

  • -25×4 er

  • -11×-11 er

Produkt#

Det viser seg at om vi multipliserer to naturlige tall får vi et naturlig tall. Multipliserer vi to heltall får vi et heltall. (Vi skal senere se at tilsvarende gjelder for rasjonale tall og reelle tall.) Vi sier at multiplikasjon er lukket i disse talltypene.

Prosesser#

Vurdere rimelighet?#