Likningsregler#
Forutsetninger og læringsmål#
Vi har snakket om likninger. Nå skal vi se på regler for å omforme en likning til en annen. Senere skal vi se på likningsløsing.
Vi snakker nå om regler som omformer en likning til en likning med like stor eller større løsningsmengde. Om premiss-likningen er sann må også konklusjonen være sann.
Oppgaver#
Introduksjon#
TODO INnsetting(substitution)#
En term (uttrykk) kan være for eksempel en likning, et bokstavuttrykk eller tall-uttrykk.
2 + 3×4: Vi kan bruke regelen {{rule(“3×4”, “12”)}} til å skrive 2 + 3×4 om til 2 + 12. Vi bruker altså regelen på en del av det opprinnelige bokstavuttrykket.
\(x + 2 = 3 + 2x - x\): Her kan vi bruke den generelle regelen {{rule(“2A - A”, “A”)}}, hvor vi setter inn \(x\) for \(A\) (og får {{rule(“2x - x”, “x”)}}), på den opprinnelige likningen. Vi får \(x + 2 = 3 + x\).
Representasjoner#
Balansevekt#
Gjøre det samme på begge sider TODO
Ord#
Premiss, konklusjon
Formelspråk#
→#
For regler bruker vi i Mashov tegnet →, f.eks. \(\overset{A - B = C}{\underset{A = B + C}{↓}}\).
Likning#
En utregning med likninger er teknisk sett implikasjoner. Likningene impliserer hverandre. Derfor brukes gjerne pil (→, ↓) eller dobbeltpil (⇒, ⇓) mellom likningene. Dette til forskjell fra utregning med bokstavuttrykk, som skal være lik hverandre, og som har likhet (=) mellom.
Koordinatsystem#
Interessant men nerdete TODO
Algoritmer#
Gjøre ting på en av sidene#
Vi har selvfølgelig lov til å bruke alle vanlige regler inni en av sidene. Vi kan gå fra
\(x + 2 = 1 + 3\) til
\(x + 2 = 4\) ved å bruke regelen \(1 + 3 → 4\).
Speile#
Om \(A\) er lik \(B\), er \(B\) lik \(A\). Vi kan si at likhets-operatoren er symmetrisk eller at den er kommutativ.
Gjøre det samme på begge sider (flytte over)#
For alle disse reglene gjelder at vi gjør det samme på begge sidene. Noen ganger sier vi at vi “flytter over og skifter fortegn”
Legge til det samme på begge sider (flytte over minus til pluss)#
La oss se på \(x - 2 = 3\).
Her kan vi velge å legge til 2 på begge sider. Vi får
1: \(x - 2 = 3\)
2: \(x - 2 + 2 = 3 + 2\) Vi har lagt til 2 på begge sider
3: \(x + 0 = 3 + 2\)
4: \(x = 5\) og vi ser løsningen.
Hvorfor velger vi å legge til akkurat 2 på hver side? Svaret er at vi velger å legge til akkurat +2 fordi vi ser det står −2 der fra før; og vi planlegger +2 og −2 skal eliminere hverandre, bli til 0 og forsvinne. Vi håndterer altså −2 ved å legge til +2 på hver linje.
I Koordinatsystem#
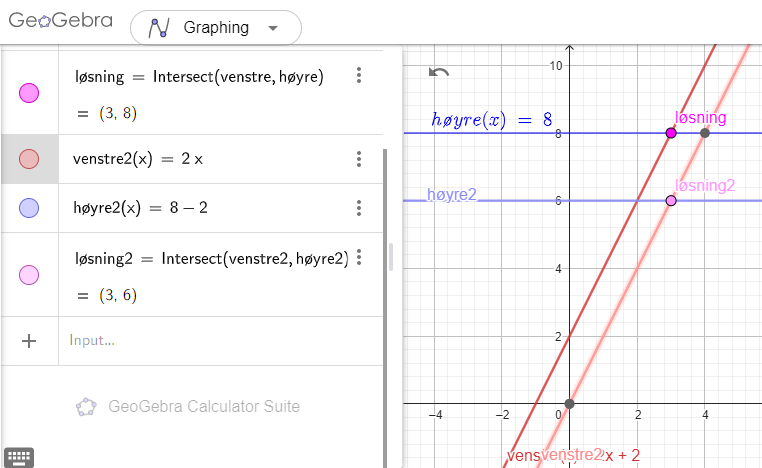
Flinke studenter kan ha glede av å studere hvordan denne regelen viser seg i koordinatsystem. Vi tegner igjen hver side for seg. Å trekke fra 2 er å gå 2 nedover. Løsningen (x ↦ 3) er den samme.
Vi kan også legge til variable#
I balansevekt-representasjonen er det greit å forstå hvorfor vi kan legge til det samme på begge sider. Vi kan legge til et tall, og om vi vil også en variabel:
\(-x + 3 = 5\)
\(-x + 3 + x = 5 + x\) Legger til \(x\)
\(3 = 5 + x\)
\(3 - 5 = 5 - 5\) Trekker fra \(5\)
\(x = 2\)
“Flytte over”#
Om vi ikke ser på linje 2, men ser direkte fra linje 1 til 3, kan det se ut til at vi har flyttet over 2-eren og skiftet fortegn. Dette kan se ut som trolldom. Som all trolldom er dette imponerende, men vanskelig å forstå. Dette trolldomstrikset, som så mange andre, består egentlig bare av lynrask fingerferdighet: Vi har egentlig vært innom linje 2, men så raskt at ingen la merke til det.
Om noen elever har laget seg en regel om å flytte over og skifte fortegn, er det greit om de forstår hvorfor. Men om de har en regel uten å forstå hvorfor, er det magi for dem.
Jeg vil oppfordre lærerstudenter til å ikke bruke flytteover-regler. Det har flere fordeler:
Det er sunt å unngå disse reglene når vi forklarer til elever som lærer dette første gang
Det hjelper oss å skjønne hva som egentlig skjer
Trekke fra det samme på begge sider (flytte over pluss til minus)#
Dette blir selvfølgelig veldig tilsvarende.
For å håndtere en pluss trekker vi fra på begge sider.
La oss se på \(x + 2 = 3\)
Dette blir veldig tilsvarende: Vi trekker fra 2 på hver side. Vi får
1: \(x + 2 = 3\)
2: \(x + 2 - 2 = 3 - 2\) Vi har lagt til 2 på begge sider
3: \(x + 0 = 3 - 2\)
4: \(x = 1\) og vi ser løsningen.
Vi håndterer altså −2 (mer generelt: −C) ved å legge til +2 (mer generelt: +C).
“Flytte over”#
Igjen kan noen elever finne på å gå rett fra linje 1 til 3 og si at de “flytter over og skifter fortegn”, denne gang fra pluss til minus. Men egentlig har vi bare trukket fra på begge sider.
Gange på begge sider (flytte dele til gange)#
La oss se på \(x ÷ 2 = 3\).
Her håndterer vi ÷2 ved å multiplisere med 2 på hver side.
Her kan vi altså gange med 2 på hver side. Dette kan tolkes som å flytte over 2-eren og skifte fortegn fra ÷ til ×.
Dele på begge sider (flytte gange til dele)#
La oss se på \(x × 2 = 3\).
Generalisering: Gjøre det samme på begge sider#
Dette ble i grunn kjedelig. Kan vi gjøre hva som helst, så lenge vi gjør det samme på begge sider? Svaret er ja, nesten. Det finnes unntak som for eksempel at man ikke kan dele på 0 på begge sider. Men når det er sagt: Enhver injektiv funksjon kan brukes på begge sider.
Eksempel: La \(F\) være funksjonen som tar et argument og legger til 2. Dette kan vi skrive \(F(x) = x + 2\). Da får vi at \(A = B → F(A) = F(B) → A + 2 = B + 2\).
Meta: Anvende en regel#
Substitusjon / innsetting TODO
Aspekter ved likningsregler#
En gyldig regel:
Om premisset er sant, er konklusjonen sann. Merk at konklusjonen kan bli sann flere ganger → økt løsningsmengde.
Minst samme løsningsmengde.
Et utsagn som er sant#
Setningen “x minus to er lik 3” er et utsagn som er sant eller ikke. Det spesielle her er at det er sant for én verdi av x og usant om andre.
En overgang mellom likninger må da tolkes som en implikasjon: Det første utsagnet impliserer det andre, det vil si at om det første utsagnet er sant må også det andre være sant.
I utregningen
1: \(x - 2 = 3\)
↓
2: \(x - 2 + 2 = 3 + 2\)
har vi at om linje 1 er sann er også linje 2 sann. Vi har altså at linje 1 impliserer linje 2.
Implikasjon skriver vi ofte med dobbeltpil: \(x - 2 = 3 ⇒ x = 5\). En implikasjon som går begge veier kalles en ekvivalens og skrives med dobbeltpil: \(x - 2 = 3 ⇔ x = 5\)
Det finnes andre typer utsagn enn likninger. Eksempler er ulikheter som \(x < 3\) og \(x ≠ 3\) (som begge er sanne for noen x og usanne for andre).
Hvilke x-er utsagnet er sant for (løsningsmengde)#
Vi kan også snakke om hvilke verdier for x som gjør utsagnet sant. Mengden av disse verdiene kalles løsningsmengden.
I utregningen
1: \(x - 2 = 3\)
↓
2: \(x - 2 + 2 = 3 + 2\)
har vi at de verdiene for x som gjør linje 1 sann er de samme som de som gjør linje 2 sann. Vi har altså at løsningsmengden for linje 1 er lik løsningsmengden for linje 2.
I noen overganger mellom likninger har vi en implikasjon som bare går én vei. Eksempel:
1: \(x = 2\) Løsnngsmengden er \({2}\)
⇓ Implikasjon, men ikke ekvivalens
2: \(x^2 = 4\) Løsningsmengden her er større! \({−2, 2}\)
Dynamisk balanse#
Sier ting om en likning. Mange av tingene vi kan omtale som likning…
