Variabel#

Forutsetninger og læringsmål#

Så langt har vi regnet med tall. Dette kalles . Nå skal vi bevege oss over til å “regne med bokstaver” , som kalles .

Vi forutsetter at du er stø i f.eks. multiplikasjon, potensregning, parenteser og resten av formelspråket. Er du ustø på disse tingene, bør du bli stø på det først.

Regneoperasjonene er de samme som før. For eksempel har vi at \(a+a+a\) kan skrives som \(3a\) og at \(\frac{a^5}{a^2}\) kan skrives som \(a^3\).

Introduksjon#

Foreløpig kan vi si at en variabel er “et ukjent tall” eller “hvilket som helst tall”.

Representasjoner#

Rinvold, 2010 i Tangenten: Konkreter i læring av algebra

Ord#

På norsk henger variabel sammen med ord som variere, hva som helst, noe og generelt. Noen skiller skarpt mellom begrepene variabel, ukjent og konstant; andre lar disse begrepene flyte mer over i herandre.

I flertall brukes både «variable» og «variabler». Språkrådet argumenterer med at det første er opprinnelige (siden variabel i utgangspunktet er et adjektiv), men argumenterer likevel for det siste (siden en variabel nå er et substantiv).

../../_images/4m1.stock-photo-match-fire-burned-matches-red.jpg

Fig. 13 Representasjon av 4−1?#

Fyrstikker: Esker 🟥#

Min favorittrepresentasjon for en variabel bygger på “fyrstikkspråket”, hvor heltall kan representeres med et antall fyrstikker. Halve kan representeres som brukne fyrstikker. Kanskje figuren til venstre kan representere 4−1?

I denne representasjonen er en variabel en fyrstikkeske. Dette illustrerer flere ting:

  • En fyrstikkeske kan inneholde et ukjent antall fyrstikker (ukjent)

  • En fyrstikkeske kan inneholde hvilket som helst antall fyrstikker (generalitet)

  • En fyrstikkeske er selv en ting som kan snakkes om; vi kan for eksempel si “tre fyrstikkesker”.

Det er da underforstått at alle like fyrstikkesker har like mange fyrstikker (alle x-er har lik verdi). Dette må tydeliggjøres for elevene.

Det går også an å ha flere typer fyrstikkesker, for eksempel med forskjellig farge.

Noen ganger vil vi symbolisere en fyrstikkeske med en farget firkant: 🟥

Penger: Konvolutter ✉#

Vi kan også bruke andre ting som kan inneholde ting, for eksempel konvolutter. Dette var særlig aktuelt i gamle dager da folk sendte brev i konvolutter og da penger var representert med papirlapper som kunne puttes oppi konvolutter.

Småstein og fliser#

I våre tegninger skal vi representere variable som små bokser med “ukjent” lengde. Hver variabel får sin faste lengde og sin farge. Vi skal vanligvis bruke representasjonene

\(a\)

\(b\)

\(x\)

\(y\)

\(m\)

\(n\)

Lengdene betyr ikke at variablene har fast, kjent verdi, men tvert imot at de varierer.

Som eksempel kan \(a\)+\(b\) representeres som .

\((x+1)×(y+2)\) kan representeres som .

Geometri#

En vanlig inngang til algebra — og bruk av algebra — er geometri. Eleven kan få en situasjon, vi får variable som lengde og bredde, og elever skal finne areal. Se [Hinna et al., 2016] kapittel 2.1 side 169 2.2.2 s.186

NDLA har oppgaver som følger denne filosofien, og som kan brukes både som introduksjon, øvelse og trening i modellering.

Figurtall #

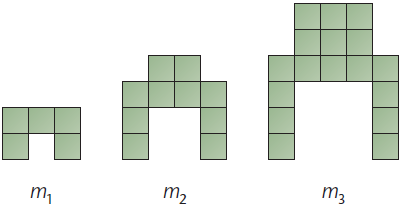
../../_images/figurtall.png
En beslektet inngang er figurtall. Eleven kan få en rekke med figurer, og skal finne antall firkanter i hvert ledd; så skal eleven generalisere til et generelt uttrykk. Denne tenkingen har stort gjennomslag i Nasjonal Deleksamen som NLA-studenter møter i MA103.

Se

Formelspråk#

I formelspråket bruker vi gjerne ord eller bokstaver. Programmerere liker å bruke lange, beskrivende ord, mens matematikere ofte liker å bruke enkeltbokstaver. n og m står gjerne for heltall. a og b står gjerne for variable, mens x og y gjerne står for ukjente. i og j brukes gjerne om såkalte indekser, til å gi nummeret i en tallrekke. Noen ganger brukes under-skrift som f.eks. n₁ eller aᵢ. I prinsippet kunne vi brukt hvilke som helst bokstav eller ord for hva som helst.

Enkeltbokstaver er raskest å skrive, men ord er ofte enklest å forstå og beholder nærheten til situasjonen. Vi burde kanskje oftere bruke beskrivende ord.

I kvalitetstypografi settes variable i kursiv. Enheter (som kg) settes derimot i normal skrift. Vi sier “høyden høyde er 170 cm” eller “l er lik 3 m”.

Algoritmer#

Egentlig samme som tall#

Man kan regne med variable på samme måte som tall. Derfor er det viktig å mestre aritmetikken før man går løs på algebra. Om man synes bokstavregning er vanskelig, er det ofte lurt å begynne med et talleksempel. Vet man ikke hva \(a - a\) er kan man først sette inn 3 for a ({a ↦3}) og se om man klarer å regnet ut \(3 - 3\); klarer man det får man kanskje en ide om hva \(a - a\) kan være. Da kan \(3 - 3\) bli et generisk eksempel.

En forskjell blir at man ofte ikke kan regne ut parenteser først. 2×(3 + 4) kan regnes ut til 2×7, mens a×(b + c) ikke kan forkortes på samme måte.

Oppgaver om bokstavregning:

Aspekter ved variable#

Variablene kan sees på forskjellige måter (aspekter). Kanskje det er noe av hemmeligheten ved å forstå algebra? Disse aspektene kommer til syne når lærere snakker om dem, så det er viktig at vi vet noe om dem.

[Küchemann, 1978] snakker om

  • Evaluated

  • Ignored

  • Object

  • Specific unknown

  • Generalized number

  • Variable

Aspektene#

En ting#

Vi kan betrakte en fyrstikkeske “utenfra”, som en ting. Da kan vi si at to fyrstikkesker pluss tre fyrstikkesker er fem fyrstikkesker. Be en elev hente 2fyrstikkesker + 3fyrstikkesker + 4fyrstikkesker, og eleven vil snart forkrote det til 9 fyrstikkesker.

Det er dette aspektet vi bruker når vi setter inn en appelsin 🍊 for a, 🍌 for b etc.

Vi må være nøye på om a representerer “én appelsin” eller om a representerer f.eks. “kiloprisen for appelsiner”. Blander vi dem får vi “fruktsalatproblemer”, beskrevet i [Hinna et al., 2016] på side 1070. Ellef mener begge betydningene er helt greie, så lenge vi ikke blander dem.

Konstant / variabel#

Noen ganger velger vi å sette navn på noe bare fordi det er praktisk. Det kan tenkes vi gjør dette selv om verdien er godt kjent. Eksempler er π, e og fysiske konstanter. Det kan hende vi sier “min alder er høyere enn din” også når vi vet hva alderene er.

Ukjent tall#

Vi kan snakke om fyrstikkesker som viser seg å ha en bestemt verdi, selv om vi ikke vet det enda. For eksempel kan vi se på utsagnet “2 fyrstikkesker tilsvarer seks fyrstikker”. Denne betydningen bruker vi ofte i likninger, og da bruker vi ofte bokstaven x.

Dete aspektet skal vi forfølge videre når vi snakker om likninger.

Variabel / generelt tall#

Vi kan betrakte en fyrstikkeske som et antall fyrstikker. Det vi sier om fyrstikkeskene er sant uansett hvor mange fyrstikker som er i hver. Det er sant for alle antall fyrstikkesker. Det er for eksempel sant at 2 fyrstikkesker + 3 fyrstikkesker = 1 fyrstikkeske + 4 fyrstikkesker uansett hvor mange fyrstikker det er i hver. Denne betydningen er forbundet med generalisering.

Dette aspektet skal vi forfølge videre når vi snakker om funksjoner.

Bruk av aspektene#

Noen ganger er en ting “mer konstant” enn andre. I utsagnet \(x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\) er det underforstått at x skal forståes som en ukjent mens a, b og c skal forståes som “mer konstante” eller variable. Det er ofte underforstått at dette er en generell formel; a, b og c har en konkret verdi i hver konkrete oppgave, mens x fortsatt kan variere i hver oppgave. Denne forskjellen blir ikke bestandig sagt, iallfall ikke på noe måte som gjør at elevene kan forstå. Innsikten blir bare formidlet gjennom eksempler. Men blir den formidlet gjennom eksempler? Du (en lærerstudent) kan fungere på hvordan du ville forstå utsagnet \(a = \frac{-b\pm\sqrt{b^2-4xc}}{2x}\). Har du en innsikt om forskjellen mellom a og x som aldri er formulert? Vi sa jo akkurat at a og x i prinsippet var et samme?

I et matematisk regnestykke har en variabel samme verdi gjennom hele. Dette er annerledes enn en variabel i (de fleste) programmeringsspråk, som kan skifte verdi ved tilordning.

Hvordan formidle algebra#

Algebra er ofte vanskelig [Kieran et al., 2016]. Kanskje skyldes dette at dette er et eksempel på generalisering.

Vi vil argumentere for at siden algebra er vanskelig bør man være nøye på å rydde andre vanskeligheter av veien. Vanskeligheter knyttet til parenteser eller formelspråk ellers bør komme før algebra. Det syndes en del mot dette. Vanskeligheter knyttet spesielt til likninger og funksjoner bør komme etter at elevene har vent seg til bokstavregning.

Referanser til dette:

Prealgebra#

Man kan bruke algebra tidligere enn man kanskje tror! Dette kalles prealgebra.

Talltyper#

Variable med tallverdier og andre verdier#

I grunnskolen snakker vi oftest om variable med tallverdier. Vi kan si at variabler som a og x har verdien av typen ℝ, mens n ofte har verdier av typen ℕ eller ℤ. Konstanten i og variablen z er komplekse tall i ℂ.

Men variable kan også ha verdier av andre typer (se også Wikipedia om variable):

Tidspunkt#

Variablen t står ofte for tidspunkt, tidsrom eller tidsintervall (tidslengde).

Python har en talltype datetime.

Vinkler#

α, β, γ etc. står ofte for vinkler. Her brukes også vₙ.

Python kan implementere vinkler som vanlige tall.

Punkter#

A, B og C brukes ofte for punkter, for eksempel i et koordinatsystem.

Python har ikke noe koordinatbegrep, men man kan bruke lister med to elementer eller importere en ferdig matematikk-pakke som numpy

Funksjoner#

Variablene f og g står ofte for funksjoner. Riktignok kan det være vanskelig å se dette i den forvirrende skrivemåten f(x).

Python er et funksjonelt programmeringsspråk, det vil si at variable kan peke på funksjoner. Dette er en veldig nyttig egenskap som vi ikke har kommet til ennå.

Operatorer#

Neppe relevant før på slutten av lærerutdanningen, når man snakker om algebraiske strukturer.

Dette er kanskje det mest spesielle: ⊕ og ⊗ står ofte for generelle operatorer og kan ha verdier som + og −. Eksempel: «Den kommutative loven for en operator ⊕ (som kan ha verdiene + eller ×) sier at a ⊕ b = b ⊕ a». Her kan vi altså putte inn f.eks. verdien × i variabelen ⊕, og få a × b = b × a. Putter vi inn verdien “er gift med” for ⊕, får vi “a er gift med b = b er gift med a”.