Oppgavesett nasjonal deleksamen
MA103 1-7

Om eBoka

Denne eBoka er resultatet av et delprosjekt under Innovative læremidler, som er et av satsningsområdene på NLA høgskolen. eBoka blir brukt i et undervisningsopplegg som går over flere uker. I hver økt får studentene får en kort felles introduksjon før de jobber med oppgavene i selvvalgte grupper. Hver økt avsluttes med en kort oppsummering.

Introduksjon

Hvordan bruke eBoka?

Under hver deloppgave finner du en video som forteller noe om hvordan deloppgaven kan løses. Du velger selv hvordan du bruker disse videoene:

• Noen føler seg usikre på matematikkfaget. De vil helst se på videoen før de løser en oppgave.
• Noen studenter føler seg ganske trygge på matematikken. De vil helst prøve å løse oppgaven først, så ser de videoen etterpå.
• Noen studenter føler seg enda tryggere på matematikken. For slike studenter kan videoene bli for omstendelige. Da holder det kanskje å se på de skriftlige løsningsforslagene. Om noen synes at også disse inneholder for mange detaljer, kan man se på sensorveiledningene som ligger på Canvas.

Det er et mål at du etter hvert skal klare å løse oppgavene på egen hånd og bli mindre avhengig av videoene. Uansett hvordan du bruker videoene, er det viktig at du lager et skriftlig løsningsforslag til hver eneste deloppgave. Løsningsforslaget bør ha den samme type kvaliteten som den man forventer i forbindelse med eksamen. Husk at du må lese oppgaveteksten nøye før du ser på videoene. Hvis du synes at det snakkes for langsomt på videoene, kan du endre avspillingshastigeten ved å trykke på tannhjulet til høyre under videoene.

Økt 1

Eksempeloppgave V20 oppgave 1

Tre venner går hver sin tur i fjellet. På et tidspunkt informerer de hverandre om høydelokalisasjonen sin i form av meter over havet:

Siri oppgir sin nåværende høyde i meter over havet.

Morten sier at hans høyde er 50 meter høyere enn Siris oppgitte høyde.

Miriam sier at høyden hun befinner seg på er to ganger Siris oppgitte høyde.

1. Vis hvordan du som lærer kan illustrere hvordan de tre vennene kan stå i forhold til hverandre i ulike situasjoner.
2. Begrunn om det er mulig at Morten og Miriam står på den samme høyden.

Eksempeloppgave V20 oppgave 6

Nedenfor ser du to figurer av fyrstikker:

Gitt følgende påstand: For å lage fyrstikkmønsteret med \(n\) kvadrater, trenger vi \(3n + 3\) fyrstikker.

Ta stilling til påstanden og begrunn med utgangspunkt i mønsteret over om påstanden er rett eller gal.

Eksempeloppgave V20 oppgave 7

Under er det tegnet tre figurer som representerer stoltallene \(S_1\), \(S_2\) og \(S_3\). Antallet prikker i figur \(1\) kaller vi for \(S_1\) (stoltall nummer \(1\) ), antallet prikker i figur \(2\) kaller vi \(S_2\) (stoltall nummer \(2\) ) og så videre.

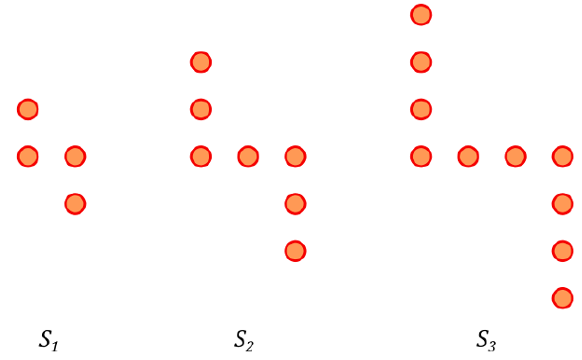
1. Bruk figurene til å forklare utviklingen til stoltallene fra \(S_1\) til \(S_3\), og tegn \(S_6\).

Klassen din arbeider med denne oppgaven. De kommer frem til to ulike formler for stoltall nummer \(n\). $$ S_n=2n+(n+1) $$ $$ S_n=2(n+1)+n-1 $$

2. Forklar hvordan begge formlene henger sammen med figurene av stoltallene, og vis algebraisk at formlene er like.
3. Tenk deg at du har \(131\) prikker til rådighet. Hvilket nummer har det største stoltallet du kan lage?
4. Finn en eksplisitt formel for tallfølgen hvor de fire første tallene er gitt ved: \(2\), \(7\), \(15\), \(26\), …
   (Hint: det kan være nyttig å bruke kvadrattall og trekanttall).

Økt 2

Oppgave om utledning av formelen for trekanttall

Målet med denne oppgaven er å lage en formel for det \( n \)’te trekanttallet, \( T_n \).

Under er det tegnet tre figurer som representerer rektangeltallene \( R_1 \), \( R_2 \) og \( R_3 \). Antallet prikker i figur \(1\) kaller vi for \( R_1 \) (rektangeltall nummer \(1\) ), antallet prikker i figur \(2\) kaller vi \( R_2 \) (rektangeltall nummer \(2\) ) og så videre.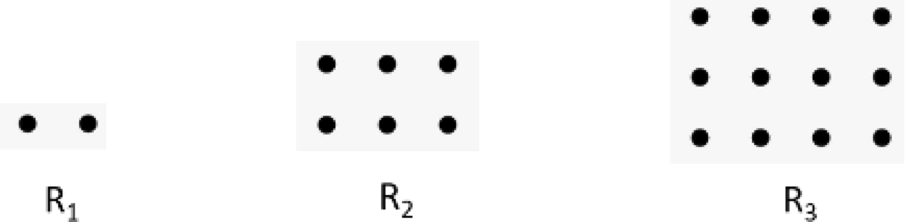

1. Bruk figurene til å forklare utviklingen til rektangeltallene fra \( R_1 \) til \( R_3 \) og tegn \( R_4 \).
2. Lag en formel for det \( n \)’te rektangeltallet \( R_n \).
3. Del figuren som representerer rektangeltallet \( R_3 \) i to deler slik at hver av de to delene består av trekanttallet \( T_3 \). Del figuren som representerer rektangeltallet \( R_2 \) i to deler slik at hver av de to delene består av trekanttallet \( T_2 \). Del figuren som representerer rektangeltallet \( R_1 \) i to deler slik at hver av de to delene består av trekanttallet \( T_1 \).
4. Bruk det du gjort i oppgave c) til å lage en formel for \(T_n\) (trekanttall nr. \(n\)).

Eksempeloppgave H19 oppgave 1

Figurene viser de tre første balansetallene \( B_1 \), \(B_2\) og \(B_3\). Mønsteret fortsetter som vist på figuren for \(𝐵_4\), \(B_5\) og så videre.

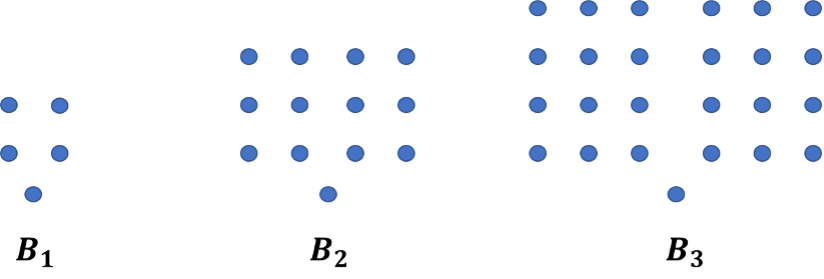
1. Forklar utviklingen til balansetallene og tegn figur \(𝐵_4\).
2. Klassen din arbeider med denne oppgaven. De kommer frem til to ulike formler for balansetall nummer n.

1. \(𝐵_𝑛 =2𝑛⋅(𝑛+1)+1\)

2. \(𝐵_𝑛 =1+2(𝑛(𝑛+1))\)

Forklar både ved en tegning og ved ord hvordan de to formlene henger sammen med figuren.

3. Vis ved algebraisk omforming at de to formlene sier det samme.
   

Økt 3

Eksamen V20 oppgave 7

Nedenfor ser du de fire første figurene i et voksende figurmønster:

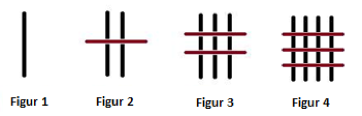
1. Beskriv utviklingen fra Figur \(3\) til Figur \(5\).
2. Forklar den generelle sammenhengen mellom figurnummeret og totalt antall streker i figuren slik du kunne ha gjort for en elev. Bestem den generelle formelen for hvor mange streker det vil være i Figur \(𝑛\).
3. Hvor mange horisontale og vertikale streker vil Figur \(99\) ha?
4. Noen foreldre er skeptisk til arbeid med figurtall slik som figurene ovenfor. De mener figurtall ikke er relevant innenfor matematikken. Gi to argumenter for hvorfor slike oppgaver innebærer algebraisk tenkning.

Eksempeloppgave H19 oppgave 5

En elev greier ikke å løse følgende oppgave: For hvilke tall \(x\) er \(2𝑥\) større enn \(𝑥 + 2\)?

Lag en tabell og skisser de to grafene i et koordinatsystem. Forklar hvordan representasjonene viser løsningen.

Eksamen V20 oppgave 5

Dag Otto er ute på en rolig sykkeltur, og grafen nedenfor beskriver turen time for time de første åtte timene.

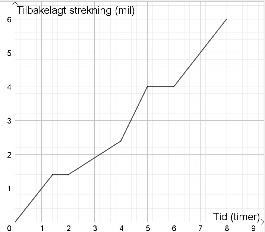
1. Noen elever sier at Dag Otto syklet raskest når han har syklet mellom \(1,4\) og \(2,0\) timer fordi grafen er kortest i dette tidsrommet. Vurder gyldigheten av resonnementet til elevene hvor du også gjør rede for det korrekte svaret. Vil det finnes tilfeller hvor et slikt resonnement stemmer? Begrunn.
2. Etter den åttende timen sykler Dag Otto samme rute hjem på tre timer. Skisser grafen for hjemturen, og kommenter en misoppfatning som kan avdekkes når elever skisserer grafen for hjemturen.
3. En annen representasjon vi har for funksjoner er funksjonsuttrykk. Avgjør og begrunn, uten å tegne grafen, om påstandene under er sanne/usanne for funksjonsuttrykket

$$𝑓(𝑥) = \frac{4}{3} (𝑥 + 2)$$

i.Funksjonen \(f\) er lineær
ii. Grafen til funksjonen \(𝑓\) skjærer \(𝑦\)-aksen i punktet \((0,43)\)
iii.Funksjonen \(𝑓\) har alltid en positiv funksjonsverdi så lenge \(x>0\)

Økt 4

Eksempeloppgave V20 oppgave 3

Martha og Louise plukket blåbær for å lage blåbærsyltetøy. Den første dagen plukket de \(23\) liter urensede bær. Den andre dagen plukket de \(39\) liter urensede bær. Under rensing begge de to dagene, kastet de like mange liter med rusk og rask av dårlige blåbær, blader og stilker. De plukket dobbelt så mange liter med renskede blåbær den andre dagen sammenliknet med den første dagen.

Hvor mange liter blåbær hadde de å lage syltetøy av hver av disse dagene? Vis løsningen ved hjelp av systematisk gjett og sjekk, og ved hjelp av likning.

Eksempeloppgave V20 oppgave 2

Følgende tekstoppgave er mangelfull: En gartner skal vanne planter i drivhuset sitt. Han bruker to kanner på å vanne tomatene, tre kanner på å vanne chilitrærne og en kanne på å vanne bønnene.

Gitt:
i. \(\:2𝑥+3𝑥+𝑥+108\)
ii. \(2𝑥+3𝑥+𝑥=108\)

1. Angi hva \(108\) representerer og still et spørsmål slik at tekstoppgaven passer til i).
2. Angi hva \(108\) representerer og still et spørsmål slik at tekstoppgaven passer til ii).

Eksempeloppgave H19 oppgave 3

En elev har løst oppgavene som vist under. Begrunn om oppgaven er korrekt løst eller ikke. Vis eventuelt korrekt løsning.

1. Trekk sammen:
   $$\frac{𝑥^2 −𝑥}{2x} = \frac{x}{2x}=\frac{1}{2}$$
2. Løs ligningen:
   \begin{align} \frac{4}{x+3}+\frac{7}{2} &= 4 \\ \\ \frac{4}{x+3} &= \frac{1}{2} \\ \\ x+3 &= 8 \\ \\ x &= 5 \end{align}

Eksempeloppgave H19 oppgave 4

Betrakt følgende oppgave: $$ 19+13 = \square +12. $$

1. Angi to tall, ett korrekt og ett ukorrekt som elever kan tenkes å fylle inn på den tomme plassen, og beskriv hvordan elevene kan ha tenkt.



En elev har regnet ut \(3 \cdot 17\) på følgende måte: $$ 3 \cdot 17 = 3 \cdot 10 + 3 \cdot 7 $$

2. Vis ved en visuell representasjon at strategien alltid gjelder for multiplikasjon av et ensifret tall med et tosifret tall.

Økt 5

Eksamen V20 oppgave 1

1. Gi et eksempel på en oppgave hvor elever som oppfatter likhetstegnet som en operator ofte vil svare feil. Gi to mulige feilsvar som elever vil kunne svare på oppgaven du har laget og forklar hvorfor elever gir disse svarene.



Elever blir bedt om å finne tallet slik at likheten i følgende oppgave er sann: $$ 10 \ – 4 = \square + 7 $$

2. Vis hvordan elever kan bruke tallinja til å løse likheten.
3. Guro har hatt en innføringstime om det å løse ligninger, og hun ga elevene følgende problem:

$$ 6 − \square = 10 − 7 $$ Hun ba elevene om å avgjøre hvilket tall som kunne skrives inn i den tomme boksen for å gjøre uttrykket sant. Alle elevene fikk det riktige svaret \(3\), men de brukte ulike strategier. Er noen av følgende strategier riktige, i så fall hvilke(n)? Begrunn svaret ditt.

Hilde: \(6\) er \(4\) mindre enn \(10\) på den andre siden. Da må jeg trekke fra \(4\) fra \(7\) for å få det samme, så svaret er \(3\).
Fredrik: Når jeg regner \(10\) minus \(7\) får jeg \(3\), så \(3\) må settes inn i den tomme boksen for å gjøre uttrykket sant.
Marit: \(10−7=3\), så jeg må finne ut hva jeg trekker fra \(6\) for å få \(3\). Siden \(6−3=3\), blir svaret \(3\).

Eksamen V20 oppgave 3

1. Forklar om følgende utsagn er alltid sant, alltid usant eller av og til sant for ulike valg av hele tall \(𝑎\) og \(𝑏\) større enn \(0\).

1. \(𝑎=𝑏\)




Forklar om følgende utsagn er alltid sant, alltid usant eller av og til sant for ulike valg av hele tall \(𝑎\) større enn \(0\).

2. Uttrykket \(𝑎 + (𝑎 + 2) + (𝑎 + 3)\) har tre ledd som alle er oddetall.

I en lærebok fra 1975 er følgende to oppgaver gitt:



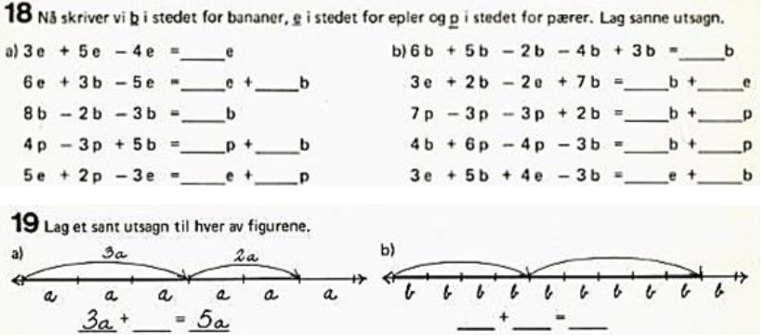
2. Forklar hvorfor oppgaveteksten i oppgave 18 er uheldig med hensyn på variabelbegrepet.


3. Lag en kontekstoppgave som passer til oppgave 19 b) som er egnet til å gi forståelse for variabelbegrepet. Forklar hvorfor \(𝑏\) er en variabel i konteksten.

Eksempeloppgave H19 oppgave 6

Elever i en klasse fikk følgende oppgave:

«Gitt at en flaske saft koster \(s\) kroner og en vaffel koster \(v\) kroner. Du kjøper to flasker saft og tre vafler. Hva kan uttrykket \(2𝑠 + 3𝑣\) stå for?»

Elevene ga følgende tolkninger av uttrykket:

Påstand 1: «To flasker saft og tre vafler»
Påstand 2: «To ganger prisen av en flaske saft pluss tre ganger prisen av en vaffel»
Påstand 3: «Antallet flasker saft og vafler jeg kjøpte»
Påstand 4: «Prisen av to flasker saft og tre vafler»

To av påstandene er korrekte og to illustrerer en misoppfatning elever kan ha knyttet til bruk av variabler. Identifiser de to korrekte påstandene, og forklar hvilken misoppfatning de to andre eksemplifiserer.

Eksempeloppgave V20 oppgave 4

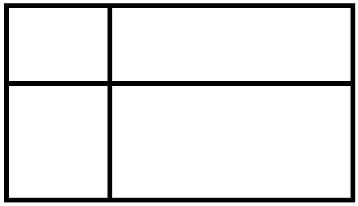
Vi har følgende likhet: $$(𝑎 + 𝑏)(𝑐 + 𝑑) = ac + bc + ad + bd,$$ der \(𝑎 > 𝑏\) og \(𝑐 > 𝑑\). Bruk rektanglet nedenfor til å vise og forklare sammenhengen ovenfor.

Økt 6

Eksamen V20 oppgave 2

Tenk på et tall, multipliser tallet med \(2\), legg til \(4\) og del svaret ditt på \(2\). Multipliser tallet du nå har med \(3\). Trekk fra det dobbelte av tallet du opprinnelig valgte, og trekk fra \(6\).

1. Vis algebraisk en generell sammenheng mellom det tallet en velger og det svaret en får.
2. Lag en «tenk på et tall»-oppgave til elever på 6. trinn hvor elevene må bruke alle de fire regneartene, og der alle elevene får samme tall som svar. Vis algebraisk at oppgaven fører til at alle elevene får samme tall som svar.

Eksamen V20 oppgave 6

En klasse arbeider med hoderegning og følgende oppgave: \(12 \cdot 5\)

1. En elevs strategi er å regne ut \(12 \cdot 5\) som \(3 \cdot 20\). Beskriv strategien eleven bruker.
2. En annen elevs strategi er å regne ut \(12 \cdot 5\) som \(10 \cdot 5 + 2 \cdot 5\). Ved hjelp av en illustrasjon, gi en begrunnelse for at det alltid er gyldig å koble sammen multiplikasjon og addisjon av naturlige tall, slik eleven her har gjort.

Eksempeloppgave V20 oppgave 5

1. Hvilke generelle sammenhenger illustrerer disse eksemplene?

$$ 18 \cdot 9 = 10 \cdot 9 + 8 \cdot 9 $$ $$ 7 \cdot 5= 7 \cdot 2 + 7 \cdot 3 $$ $$ 12 \cdot 11 = 11 \cdot 7 + 11 \cdot 5$$



2. Uten å regne, slå fast om følgende likhet er sann eller usann og begrunn svaret ditt ved hjelp av en illustrasjon:

$$ 78 + 88 = 77 + 89 $$

Eksempeloppgave H19 oppgave 2

Begrunn for hver av de følgende utsagnene om de er alltid sanne, alltid usanne eller av og til sanne for ulike valg av hele tall \(𝑎\), \(𝑏\) som er større enn \(0\).

1. \(4+𝑎=4+𝑏\)
2. \(2𝑎+3=2𝑎–3\)
3. \(𝑎\) addert med \(𝑎 + 3𝑏\) gir \(2𝑎 + 3𝑏\)
4. \(b\) addert med \(8\) gir \(8𝑏\)

Eksamen V20 oppgave 4

En elev skal vise at summen av et tilfeldig partall og et tilfeldig oddetall alltid er et oddetall. Eleven lager illustrasjon under og skriver \(2𝑛 + 2𝑛 + 1 = 4𝑛 + 1 = 2(2𝑛) + 1\).

Elevens besvarelse er ufullstendig. Forklar og vis hvilken justering som må gjøres i den algebraiske og i den geometriske representasjonen slik at begge representasjonene generaliserer at summen av et tilfeldig partall og et tilfeldig oddetall alltid er et oddetall.

Eksamen V20 oppgave 8

Følgende oppgave er en del av digitale ressurser for 6. trinn i et norsk læreverk:

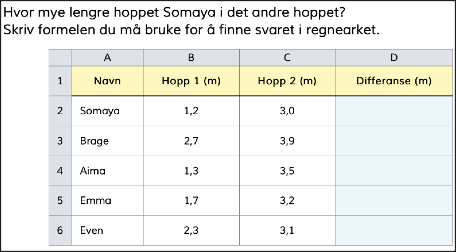
1. Redegjør for hvilke aspekter ved algebraisk tenking som kan fremmes under arbeid med regneark i oppgaven over.
2. Skisser et ekstraspørsmål som kan utvide oppgaven videre i retning av algebraisk tenking.